 測度論
測度論 「ほとんど至る所」の定義・具体例・応用|測度空間の零集合
ルベーグ積分では零集合上でのみ例外であることを「ほとんど至る所で」と言います.この記事では「ほとんど至る所で」の定義と具体例を解説したのち,ほとんど至る所で等しい関数の同一視についても解説します.
 測度論
測度論  測度論
測度論  ルベーグ積分の基本
ルベーグ積分の基本  ルベーグ積分の基本
ルベーグ積分の基本 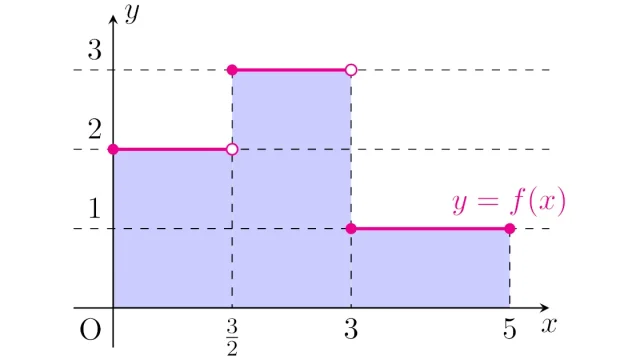 ルベーグ積分の基本
ルベーグ積分の基本 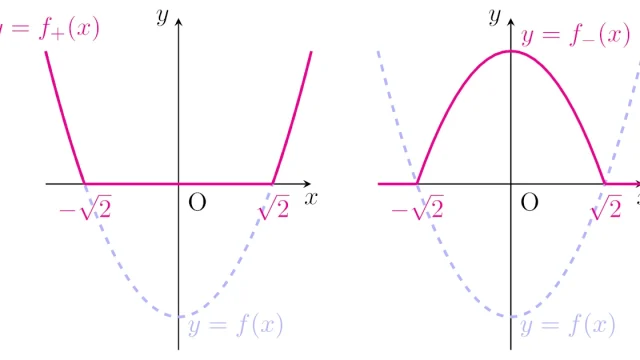 ルベーグ積分の基本
ルベーグ積分の基本 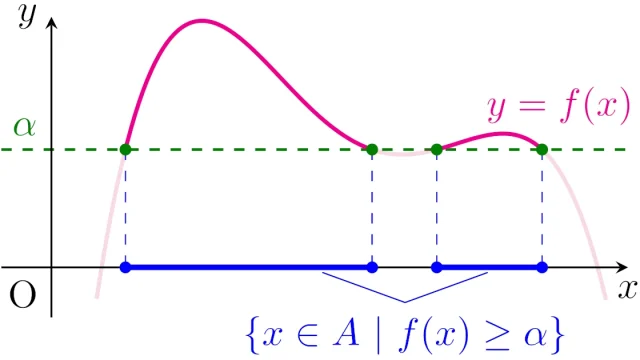 ルベーグ積分の基本
ルベーグ積分の基本 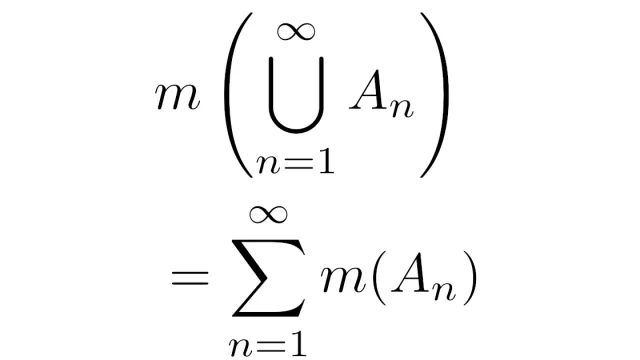 ルベーグ積分の基本
ルベーグ積分の基本 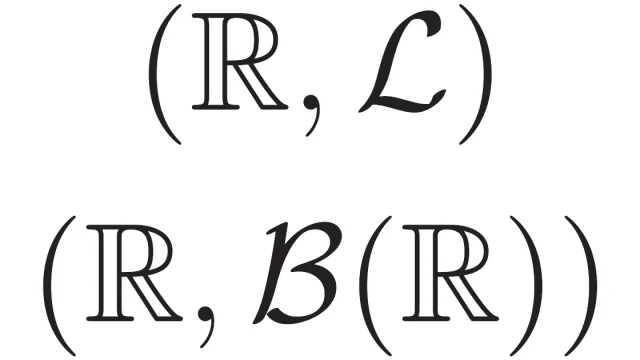 ルベーグ積分の基本
ルベーグ積分の基本 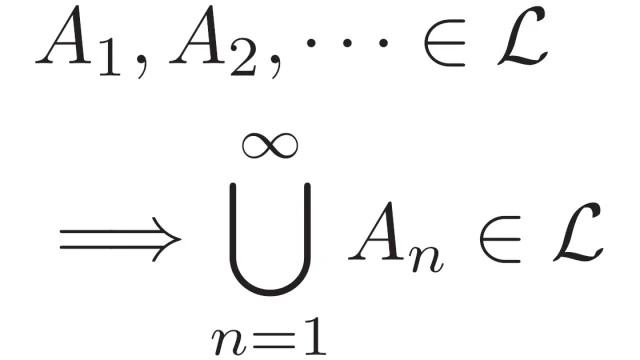 ルベーグ積分の基本
ルベーグ積分の基本