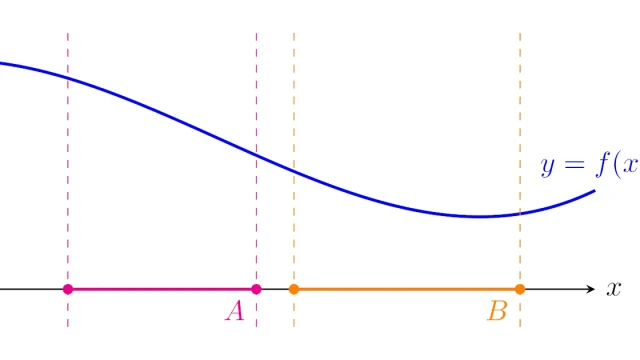
 ルベーグ積分の基本
ルベーグ積分の基本 ルベーグ積分の基本性質|非負値可測関数のルベーグ積分
非負値可測関数に対してルベーグ積分の性質から,一般の可測関数のルベーグ積分でも同様の性質が成り立つことが多いです.この記事では,非負値可測関数の性質を中心に,ルベーグ積分の基本性質を証明します.
 ルベーグ積分の基本
ルベーグ積分の基本 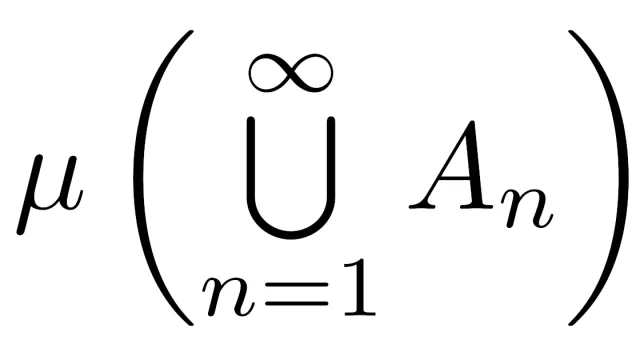 測度論
測度論 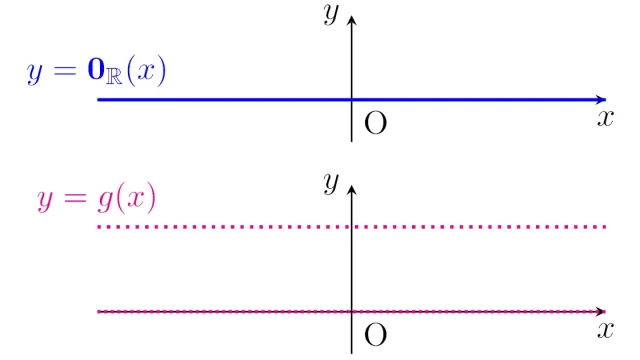 測度論
測度論 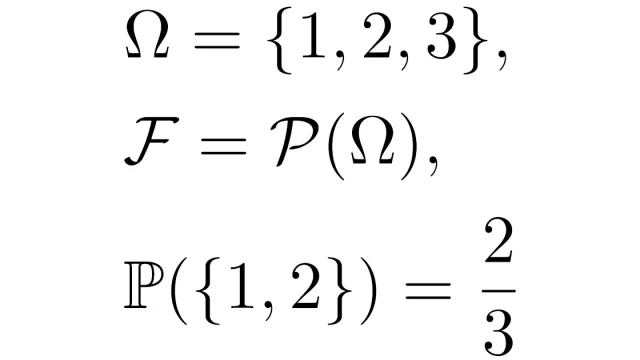 測度論
測度論 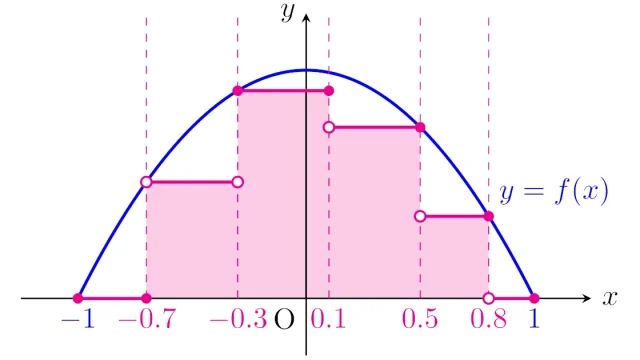 ルベーグ積分の基本
ルベーグ積分の基本 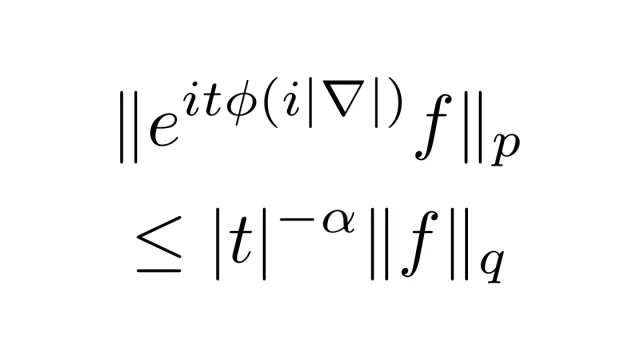 偏微分方程式
偏微分方程式 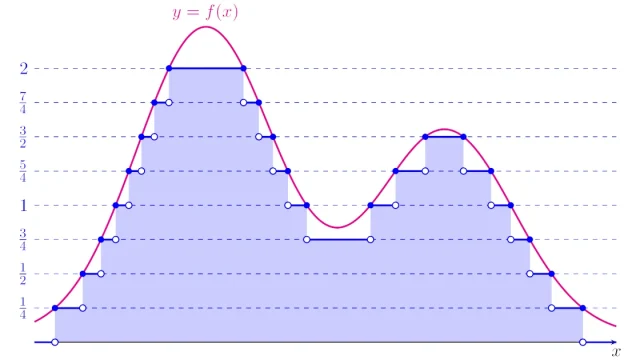 ルベーグ積分の基本
ルベーグ積分の基本 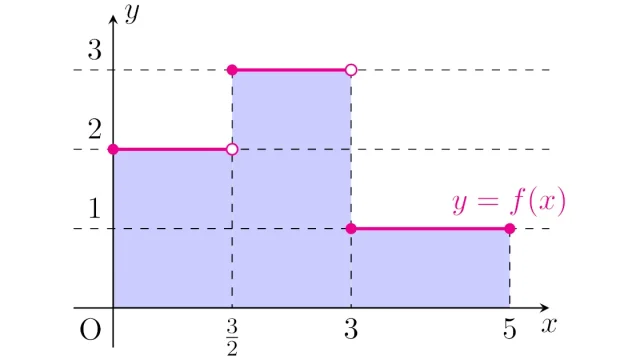 ルベーグ積分の基本
ルベーグ積分の基本 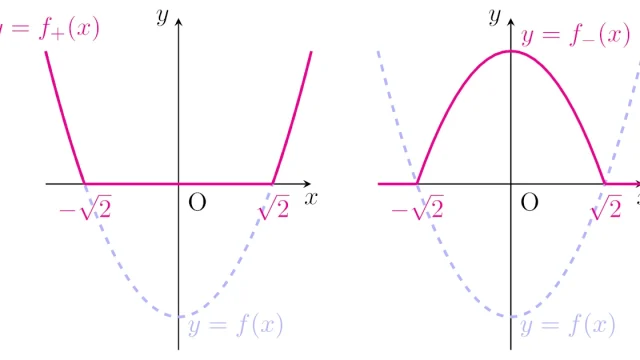 ルベーグ積分の基本
ルベーグ積分の基本 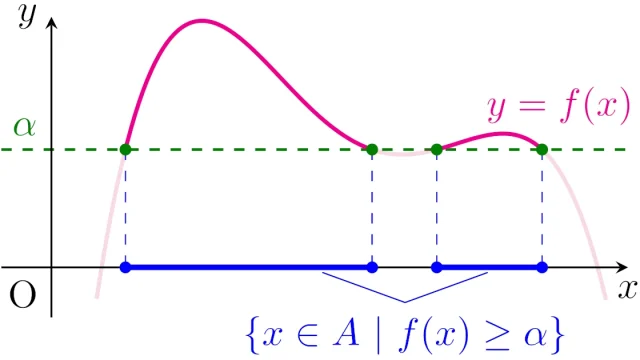 ルベーグ積分の基本
ルベーグ積分の基本