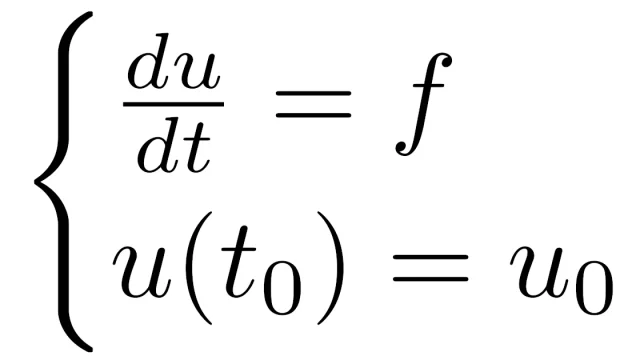 常微分方程式
常微分方程式 ピカール-リンデレフの定理|常微分方程式の解の一意存在性
常微分方程式の初期値問題の解の存在と一意性に関する重要定理としてピカール-リンデレフの定理があります.この記事では,ピカール-リンデレフの定理がどのような定理かを説明し,この定理を証明します.
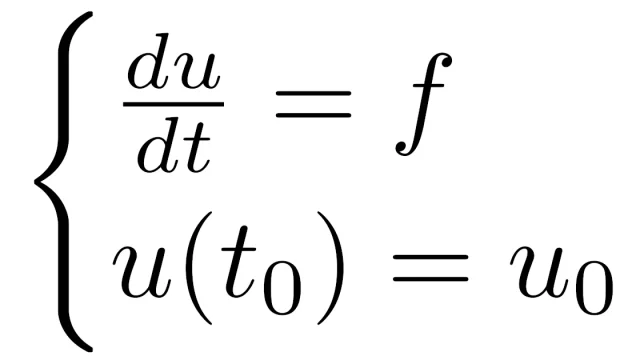 常微分方程式
常微分方程式 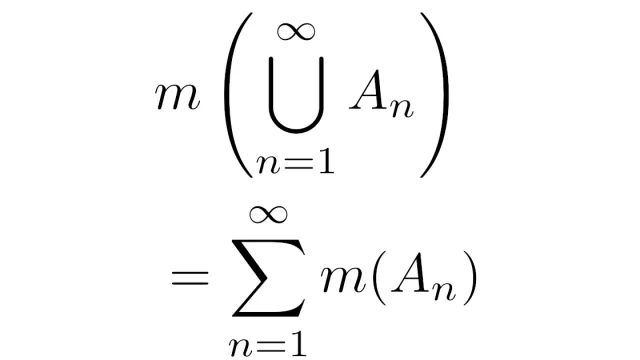 ルベーグ積分の基本
ルベーグ積分の基本 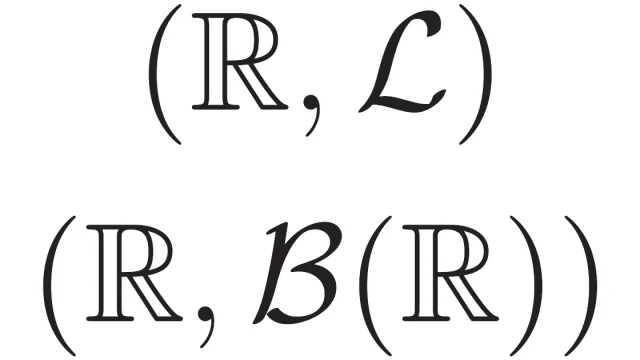 ルベーグ積分の基本
ルベーグ積分の基本 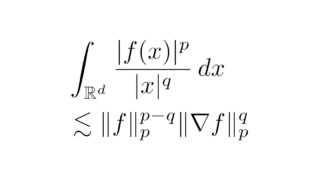 関数空間
関数空間 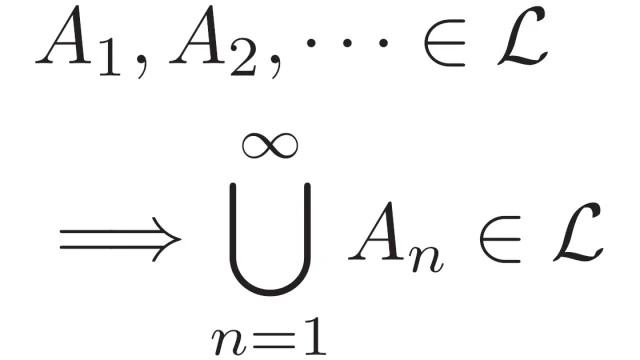 ルベーグ積分の基本
ルベーグ積分の基本 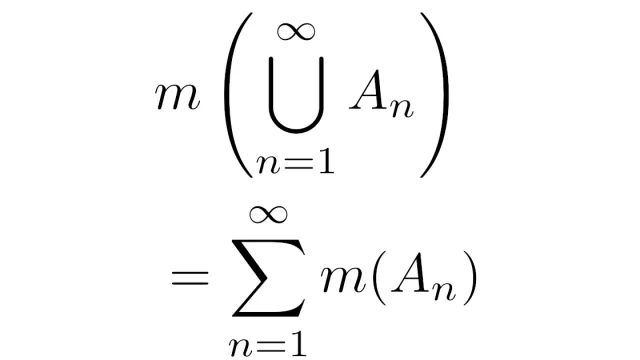 ルベーグ積分の基本
ルベーグ積分の基本 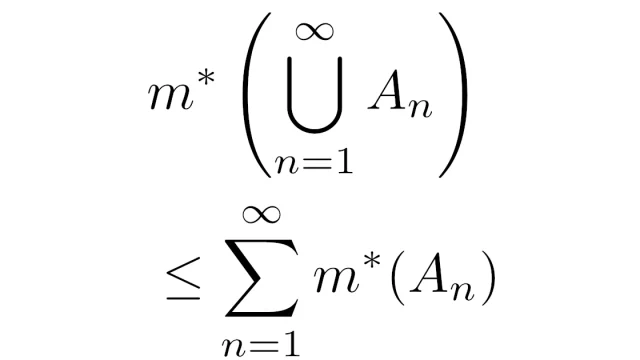 ルベーグ積分の基本
ルベーグ積分の基本  ルベーグ積分の基本
ルベーグ積分の基本  偏微分方程式
偏微分方程式 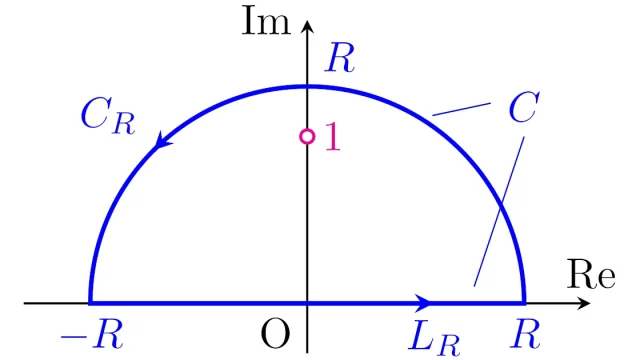 複素解析の基本
複素解析の基本