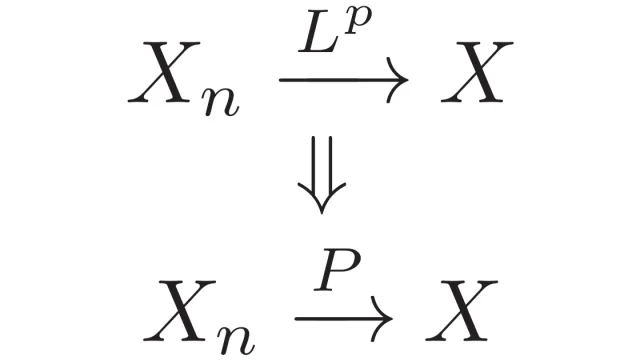 確率論
確率論 確率変数の4つの収束|概収束,平均収束,確率収束,分布収束
確率変数列の収束には「概収束」「平均収束」「確率収束」「分布収束(法則収束)」の4つが基本的で,これらの間には強弱の差があります.この記事では,これら4つの収束について説明し,これらの収束の強弱を証明します.
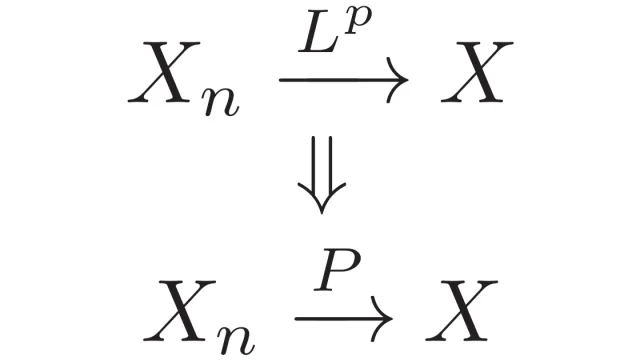 確率論
確率論 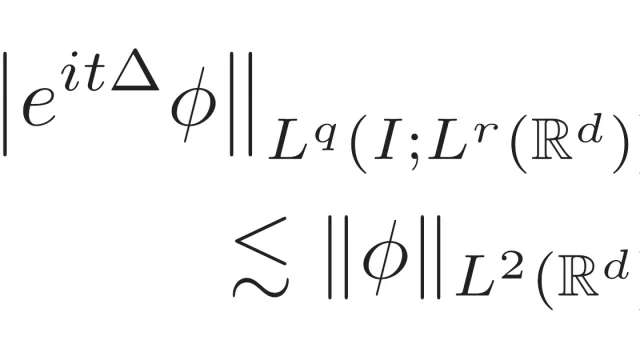 偏微分方程式
偏微分方程式 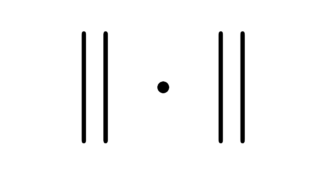 関数解析
関数解析 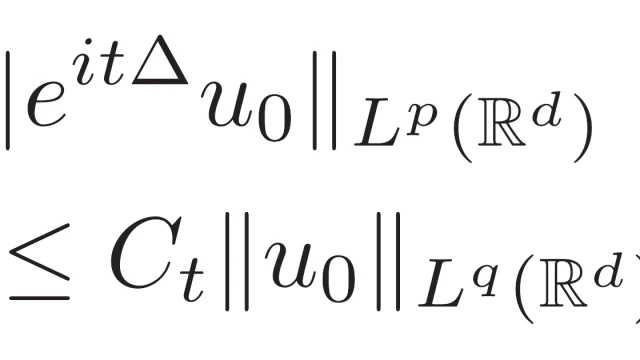 偏微分方程式
偏微分方程式 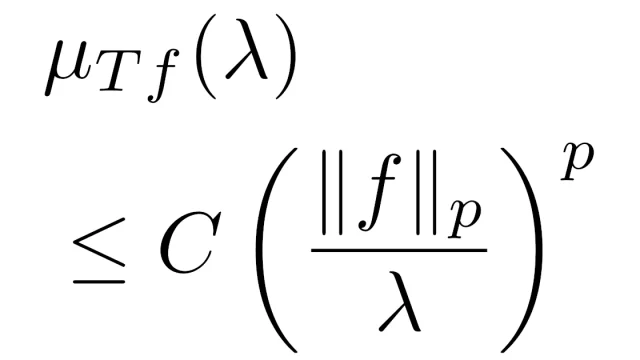 関数解析
関数解析 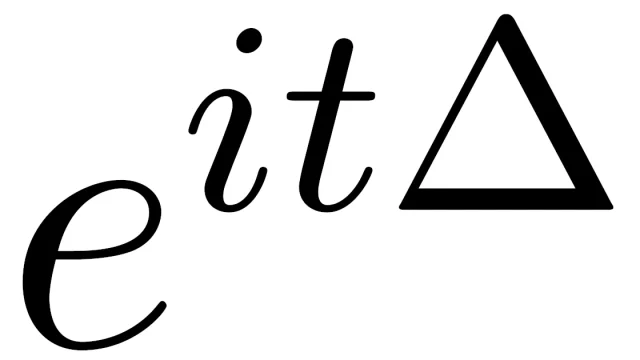 偏微分方程式
偏微分方程式  関数解析
関数解析 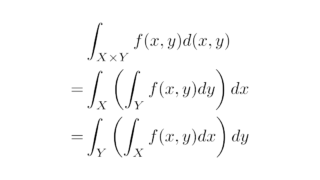 ルベーグ積分
ルベーグ積分  関数解析
関数解析  関数解析
関数解析