 線形代数学の基本
線形代数学の基本 ℝⁿの部分空間の基底と次元を求める方法を具体例から解説
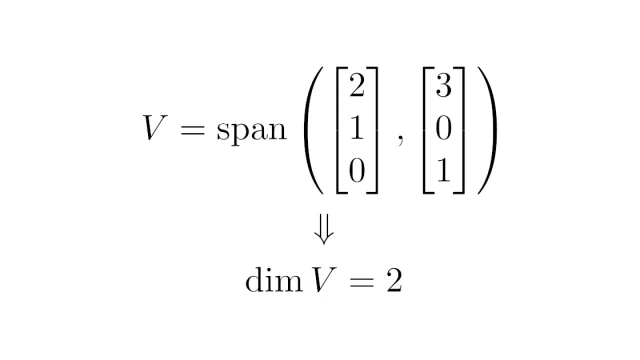
ℝⁿの部分空間Vの基底をなすベクトルの個数をVの次元といいます.この記事では$\R^n$の部分空間の次元の定義を説明し,具体例から次元の求め方を説明しています.また,基底をなすベクトルの個数が一定であることの証明もしています.
 線形代数学の基本
線形代数学の基本 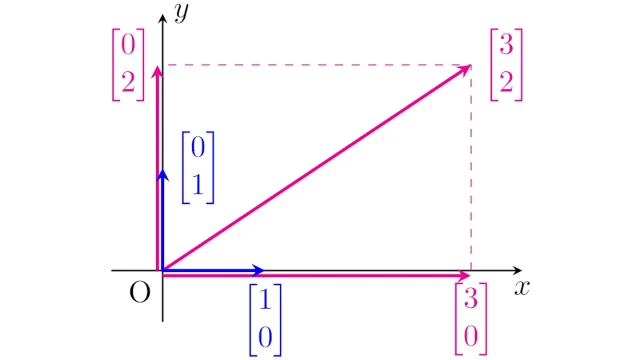 線形代数学の基本
線形代数学の基本 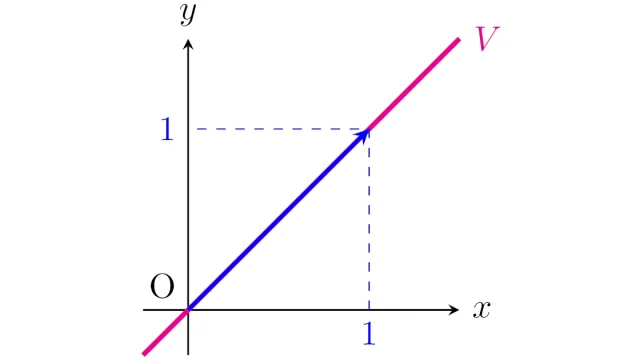 線形代数学の基本
線形代数学の基本 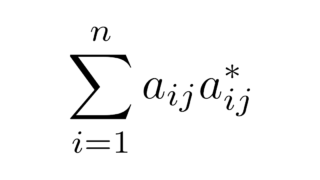 線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本 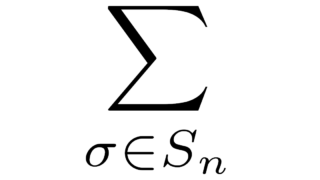 線形代数学の基本
線形代数学の基本 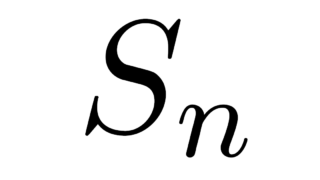 線形代数学の基本
線形代数学の基本 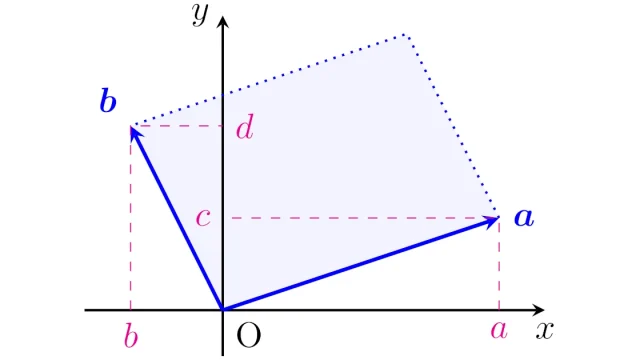 線形代数学の基本
線形代数学の基本 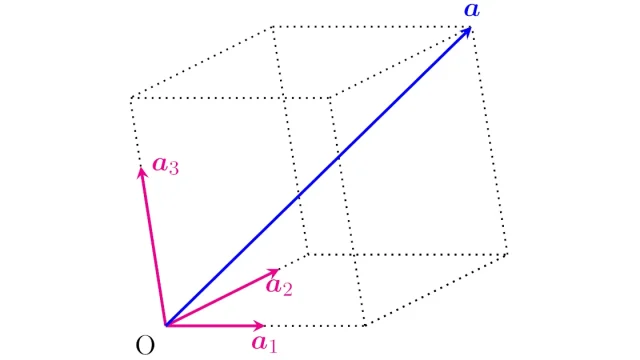 線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本