ルベーグ積分(測度論)を扱う分野では,$p$乗可積分に関する不等式であるミンコフスキー(Minkowski)の不等式がよく用いられます.
ミンコフスキーの不等式を用いると$p$乗可積分関数$f,g$の和$f+g$が可積分であることを証明できるなど,ルベーグ積分において基本的な不等式のひとつです.
また,基本的な和に関するミンコフスキーの不等式とともに,積分形のミンコフスキーの不等式も知っておきたいところです.
この記事では,
- 和のミンコフスキーの不等式
- 積分形のミンコフスキーの不等式
を順に説明します.
「ルベーグ空間$L^p$の基本」の一連の記事
和のミンコフスキーの不等式と証明
次の不等式をミンコフスキーの不等式といいます.
[ミンコフスキーの不等式]$A\subset\R$を可測集合とし,$p\ge1$とする.このとき,$A$上の可測関数$f,g$に対して,不等式
\begin{align*}\bra{\int_{A}|f(x)+g(x)|^p\,dx}^{1/p}\le\bra{\int_{A}|f(x)|^p\,dx}^{1/p}+\bra{\int_{A}|g(x)|^p\,dx}^{1/p}\end{align*}
が成り立つ.
ミンコフスキーの不等式から$p$乗可積分関数の和も$p$乗可積分関数であることが従いますね.
$p=1$のときは,任意の$x\in A$に対して,三角不等式より$|f(x)+g(x)|\le|f(x)|+|g(x)|$が成り立つから,両辺を$A$上で積分してミンコフスキーの不等式が成り立つ.
また,$\int_{A}|f(x)+g(x)|^p\,dx=0$のときもミンコフスキーの不等式が成り立つ.
よって,以下では残る$p>1$かつ$\int_{A}|f(x)+g(x)|^p\,dx>0$のときを示す.
ステップ1($f+g$の可積分性)
$\frac{1}{p}+\frac{1}{q}=1$により$q>1$を定める.任意の$x\in A$に対して,
\begin{align*}|f(x)+g(x)|^p&\le\max{\{|2f(x)|^p,|2g(x)|^p\}}
\\&\le|2f(x)|^p+|2g(x)|^p
\\&=2^p(|f(x)|^p+|g(x)|^p)\end{align*}
が成り立ち,$f,g$が$p$乗可積分関数であることから$f+g$も$p$乗可積分関数である.
また,$\frac{1}{p}+\frac{1}{q}=1$の両辺に$pq$をかけて整理すると$q(p-1)=p$となるから,$|f+g|^{p-1}$は$q$乗可積分関数である.
ステップ2($|f||f+g|^{p-1}$と$|g||f+g|^{p-1}$の積分の評価)
ステップ1と$f$が$p$乗可積分であることを併せて,ヘルダーの不等式より
\begin{align*}&\int_{A}|f(x)||f(x)+g(x)|^{p-1}\,dx
\\&\le\bra{\int_{A}|f(x)|^{p}\,dx}^{1/p}\bra{\int_{A}|f(x)+g(x)|^{q(p-1)}\,dx}^{1/q}
\\&\le\bra{\int_{A}|f(x)|^{p}\,dx}^{1/p}\bra{\int_{A}|f(x)+g(x)|^{p}\,dx}^{1/q}\end{align*}
が従い,同様に
\begin{align*}&\int_{A}|g(x)||f(x)+g(x)|^{p-1}\,dx
\\&\le\bra{\int_{A}|g(x)|^{p}\,dx}^{1/p}\bra{\int_{A}|f(x)+g(x)|^{p}\,dx}^{1/q}\end{align*}
が従う.
ステップ3($|f+g|^p$の積分の評価)
三角不等式より
\begin{align*}|f(x)+g(x)|^p&=|f(x)+g(x)||f(x)+g(x)|^{p-1}
\\&\le(|f(x)|+|g(x)|)|f(x)+g(x)|^{p-1}\end{align*}
である.この両辺を$A$上で積分してステップ2を併せると
\begin{align*}&\int_{A}|f(x)+g(x)|^p\,dx
\\&\le\int_{A}|f(x)||f(x)+g(x)|^{p-1}\,dx
\\&\quad+\int_{A}|g(x)||f(x)+g(x)|^{p-1}\,dx
\\&\le\brb{\bra{\int_{A}|f(x)|^{p}\,dx}^{1/p}+\bra{\int_{A}|g(x)|^{p}\,dx}^{1/p}}
\\&\quad\times\bra{\int_{A}|f(x)+g(x)|^{p}\,dx}^{1/q}\end{align*}
が成り立つ.ステップ1から$\int_{A}|f(x)+g(x)|^p\,dx<\infty$だから,両辺を$\bra{\int_{A}|f(x)+g(x)|^{p}\,dx}^{1/q}$で割って,
\begin{align*}&\bra{\int_{A}|f(x)+g(x)|^p\,dx}^{1-(1/q)}
\\&\le\bra{\int_{A}|f(x)|^{p}\,dx}^{1/p}+\bra{\int_{A}|g(x)|^{p}\,dx}^{1/p}\end{align*}
となり,左辺の冪$1-\frac{1}{q}$は$\frac{1}{p}$に等しいからミンコフスキーの不等式を得る.
帰納的に次の不等式が成り立ちますね.
$A\subset\R$を可測集合とし,$p\ge1$とする.このとき,$A$上の可測関数$f_1,f_2,\dots,f_n$に対して,不等式
\begin{align*}\bra{\int_{A}\abs{\sum_{k=1}^{n}f_k(x)}^p\,dx}^{1/p}
\le\sum_{k=1}^{n}\bra{\int_{A}|f_k(x)|^p\,dx}^{1/p}\end{align*}
が成り立つ.
積分形のミンコフスキーの不等式
内側が和ではなく積分となっている次の不等式もミンコフスキーの不等式といいます.
[ミンコフスキーの不等式]$A,B\subset\R$を可測集合とし,$q\ge p\ge1$とする.このとき,$A\times B$上の可測関数$f$に対して,不等式
\begin{align*}\bra{\int_{A}\bra{\int_{B}|f(x,y)|^p\,dx}^{q/p}\,dy}^{1/q}
\le\bra{\int_{B}\bra{\int_{A}|f(x,y)|^q\,dy}^{p/q}\,dx}^{1/p}\end{align*}
が成り立つ.
こちらのミンコフスキーの不等式での積分もルベーグ積分として考えていますが,より一般に$\sigma$-有限測度空間上で同様に成り立ちます.測度空間を$\sigma$-有限に限る理由はトネリの定理(フビニの定理)を用いるためです.
単純な積分の順序交換をしたいときはトネリの定理(フビニの定理)がありますが,最初の積分に冪がかかっており単純にトネリの定理が使えない場合には,積分形のミンコフスキーの不等式が便利なことがあります.
積分形のミンコフスキーの不等式は,外側の指数の方が大きければ($q\ge p$なら),指数も含めて積分の順序交換すると大きくなるという不等式ですね.
$p=q$のときは
\begin{align*}\bra{\int_{A}\bra{\int_{B}|f(x,y)|^p\,dx}\,dy}^{1/p}
\le\bra{\int_{B}\bra{\int_{A}|f(x,y)|^p\,dy}\,dx}^{1/p}\end{align*}
を示せば良いが,これは積分の順序交換に関するトネリの定理より等号で成り立つ.よって,以下では$q>p$の場合を示す.
ステップ1($p=1$の場合)
$p=1$とし,$q$のヘルダー共役を$q’$とする:$\frac{1}{q}+\frac{1}{q’}=1$.
双対性議論より,左辺$\bra{\int_{A}\bra{\int_{B}|f(x,y)|\,dx}^{q}\,dy}^{1/q}$は,可測関数$g$が$\bra{\int_{A}|g(x)|^{q’}\,dy}^{1/q’}=1$を満たしながら動くときの
\begin{align*}\int_{A}\abs{g(y)\int_{B}|f(x,y)|\,dx}\,dy
=\int_{A}\bra{\int_{B}|f(x,y)g(y)|\,dx}\,dy\end{align*}
の上限に一致する.トネリの定理とヘルダーの不等式より
\begin{align*}&\int_{A}\bra{\int_{B}|f(x,y)g(y)|\,dx}\,dy
=\int_{B}\bra{\int_{A}|f(x,y)g(y)|\,dy}\,dx
\\&\le\int_{B}\bra{\int_{A}|f(x,y)|^q\,dy}^{1/q}\bra{\int_{A}|g(y)|^{q’}\,dy}^{1/q’}\,dx\end{align*}
であることと併せて,
\begin{align*}\bra{\int_{A}\bra{\int_{B}|f(x,y)|\,dx}^{q}\,dy}^{1/q}
\le\int_{B}\bra{\int_{A}|f(x,y)|^q\,dy}^{1/q}\,dx\end{align*}
が従う.
ステップ2(一般の場合)
$\sigma:=q/p$, $F:=|f|^p$とする.$\sigma>1$だから,ステップ1より
\begin{align*}&\bra{\int_{A}\bra{\int_{B}|f(x,y)|^p\,dx}^{q/p}\,dy}^{1/q}
=\bra{\int_{A}\bra{\int_{B}F(x,y)\,dx}^{\sigma}\,dy}^{1/p\sigma}
\\&\le\bra{\int_{B}\bra{\int_{A}F(x,y)^{\sigma}\,dy}^{1/\sigma}\,dx}^{1/p}
=\bra{\int_{B}\bra{\int_{A}|f(x,y)|^{q}\,dy}^{p/q}\,dx}^{1/p}\end{align*}
が従う.

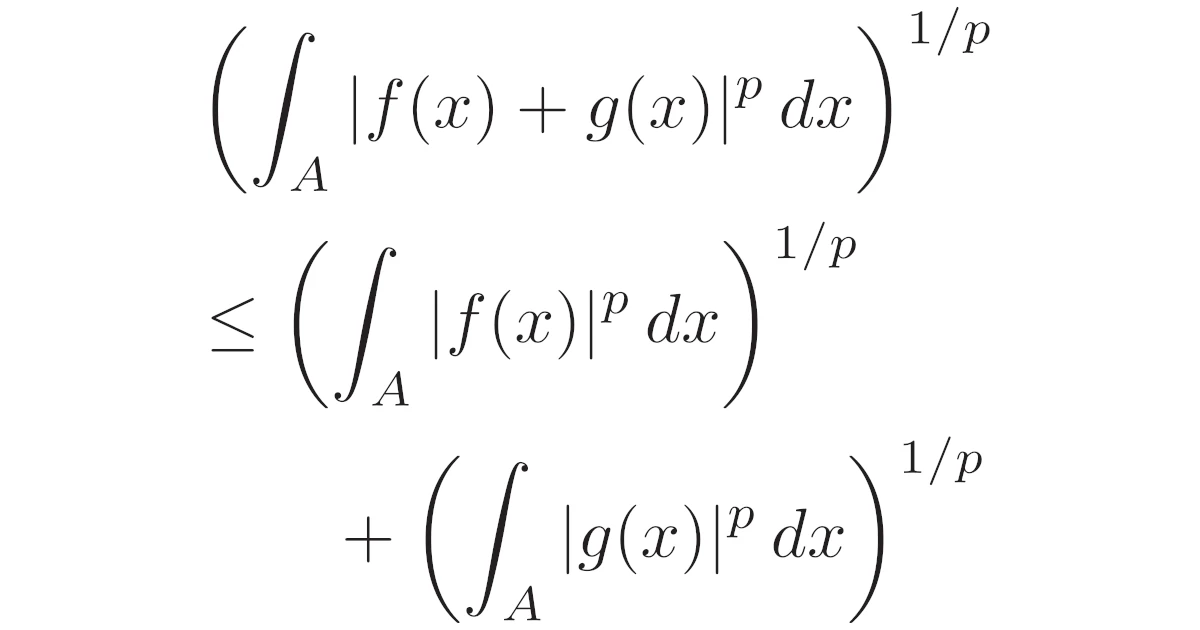


コメント
積分形のミンコフスキーの不等式についての質問です.
普通のミンコフスキーの不等式(この記事では系として紹介されている命題)の形と比較すると,$p=q$の場合,積分形のミンコフスキーの不等式の右辺の$1/p$乗は$x$についての積分の外ではなく中に掛かってくる気がしています.
自分の勘違いなのか,記事で紹介されている話とはまた別の話になるのかあまりよく分かっていません.
ご質問ありがとうございます.系の和のミンコフスキーの不等式は積分の中身が1乗和なので,積分形では左辺の中身の積分が1乗のミンコフスキーの不等式と対応します:
\begin{align*}\bra{\int_{A}\bra{\int_{B}|f(x,y)|\,dx}^{p}\,dy}^{1/p}
\le\int_{B}\bra{\int_{A}|f(x,y)|^p\,dy}^{1/p}\,dx\end{align*}
$B$での積分を和に変えると(測度論的には計数測度にすると),和のミンコフスキーの不等式になることが分かると思います.
なるほど,確かにp=qではなく,p=1で対応していますね.
理解できました.お答えいただきありがとうございます!