未知数$x_1,\dots,x_n$の連立1次方程式
\begin{align*}\begin{cases}
a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=c_1\\
a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=c_2\\
\qquad\vdots\\
a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n=c_n
\end{cases}\end{align*}
を考えます.この連立1次方程式の解が一意に定まるときには,クラメールの公式を用いることによって解を求めることができます.
クラメールの公式は線形代数の行列式を用いて連立1次方程式の解を表す定理で,うまくハマれば簡単に解を求められることもあります.
この記事では
- 連立1次方程式の予備知識
- クラメールの公式の主張・証明・具体例
- クラメールの公式の具体例
の順に説明していきます.
なお,この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが,複素行列など一般の体を成分とする行列・ベクトルに対しても同様です.
連立1次方程式の予備知識
クラメールの公式を理解するために,連立1次方程式の解が一意に定まるための条件について復習しておきましょう.
係数行列・拡大係数行列と解の存在
例えば,$x,y,z$の連立1次方程式
\begin{align*}\begin{cases}2x+3y+z=1\\-x+y-2z=-2\\2x+3y-z=-1\end{cases}\end{align*}
は行列とベクトルを用いて,
\begin{align*}\bmat{2&3&1\\-1&1&-2\\2&3&-1}\bmat{x\\y\\z}=\bmat{1\\-2}\end{align*}
と表すことができますね.
このように,一般に連立1次方程式は$A\m{x}=\m{c}$と表すことができ,この解$\m{x}$の存在は係数行列$A$と拡大係数行列$[A,\m{c}]$を用いて以下のように述べることができるのでした.
[連立1次方程式の解の一意存在]$m\times n$行列$A$と,$m$次列ベクトル$\m{c}$に対し,次は同値である.
- $\rank{A}=\rank{[A,\m{c}]}=n$が成り立つ.
- 連立1次方程式$A\m{x}=\m{c}$の解$\m{x}\in\R^{m}$が一意に存在する.
正方行列が正則であるための必要十分条件
クラメールの公式を理解するために,正方行列に関する次の定理も思い出しておきましょう.
[正方行列の正則条件]$n$次正方行列に対して,次は全て互いに同値である.
正方行列の正則条件は色々ありますが,いま述べた正則条件はランク・行列式を用いたものですね.
正方行列を係数行列とする連立1次方程式の解
以上の2つの定理から,クラメールの公式のベースとなる定理が得られます.
$n$次正則行列$A$に対して,$|A|\neq0$なら連立1次方程式$A\m{x}=\m{c}$の解$\m{x}$は一意に存在する.
連立1次方程式$A\m{x}=\m{c}$の係数行列$A$と拡大係数行列$[A,\m{c}]$について,
- 一般に行列の列に新たな列を追加しても行列のランクは下がらないから,$\rank{A}\le\rank{[A,\m{c}]}$が成り立つ
- 仮定の$|A|\neq0$に注意すると,[正方行列の正則条件]の定理より$\rank{A}=n$が成り立つ
- 拡大係数行列$[A,\m{c}]$は$n$行からなる行列だから$\rank{[A,\m{c}]}\le n$が成り立つ
これらを併せて
\begin{align*}n=\rank{A}\le\rank{[A,\m{c}]}\le n\end{align*}
となり,この最左辺と最右辺はともに$n$で等しいから,全て等しく$\rank{[A,\m{c}]}=\rank{A}=n$が成り立つ.
よって,[連立1次方程式の解の一意存在]の定理より,連立1次方程式$A\m{x}=\m{c}$の解は一意に存在する.
クラメールの公式の主張と証明
いま示した系より,$A$が正則な場合の連立1次方程式$A\m{x}=\m{c}$は一意解を持ちます.
この一意解を行列式で表す定理がクラメール(クラメル,Cramer)の公式です.
[クラメールの公式]$n$次正則行列$A=[\m{a}_1,\dots,\m{a}_n]$と$n$次列ベクトル$\m{c}$に対して,連立1次方程式$A\m{x}=\m{c}$の解$\m{x}=\bmat{x_1\\\vdots\\x_n}$は次で与えられる:
\begin{align*}x_k=\frac{1}{|A|}|\m{a}_1,\dots,\m{a}_{k-1},\m{c},\m{a}_{k+1},\dots,\m{a}_n|\quad(k=1,\dots,n)\end{align*}
$A=(a_{ij})$, $\m{c}=\bmat{c_1\\\vdots\\c_n}$と成分をおく.また,$A$の$(i,j)$余因子を$a_{ij}^{*}$とおく.
$A$は正則行列だから,連立1次方程式$A\m{x}=\m{c}$の解は
\begin{align*}\m{x}&=A^{-1}\m{c}
=\frac{1}{|A|}\bmat{a_{11}^{*}&\dots&a_{n1}^{*}\\\vdots&\ddots&\vdots\\a_{1n}^{*}&\dots&a_{nn}^{*}}\bmat{c_1\\\vdots\\c_n}
\\&=\frac{1}{|A|}\bmat{c_1a_{11}^{*}+\dots+c_na_{n1}^{*}\\\vdots\\c_1a_{1n}^{*}+\dots+c_na_{nn}^{*}}\end{align*}
となる.任意の$i\in\{1,2,\dots,n\}$に対して,余因子展開より
\begin{align*}c_1a_{1k}^{*}+\dots+c_na_{nk}^{*}=|\m{a}_1,\dots,\m{a}_{k-1},\m{c},\m{a}_{k+1},\dots,\m{a}_n|\end{align*}
となるから,解$\m{x}$の第$k$成分は
\begin{align*}x_k=\frac{1}{|A|}|\m{a}_1,\dots,\m{a}_{k-1},\m{c},\m{a}_{k+1},\dots,\m{a}_n|\end{align*}
となる.
クラメールの公式の具体例
それではクラメールの公式の具体例を考えましょう.
具体例1(未知数が2つの連立1次方程式)
$x$, $y$の連立1次方程式
\begin{align*}\begin{cases}2x+3y=-1\\5x-2y=1\end{cases}\end{align*}
を解け.
もちろん加減法(掃き出し法)によっても解けますが,方程式が2本,未知数も2個で,係数行列が正則行列であることが分かるのでクラメールの公式が使えます.
係数行列を$A$とする.$A$の行列式は
\begin{align*}|A|&=\vmat{2&3\\5&-2}=2\cdot(-2)-3\cdot5=-19\end{align*}
である.$|A|\neq0$(すなわち$A$は正則)だから,クラメールの公式が適用できて,解は
\begin{align*}
(x,y)&=\bra{\frac{1}{|A|}\vmat{-1&3\\1&-2},\frac{1}{|A|}\vmat{2&-1\\5&1}}
\\&=\bra{\frac{(-1)\cdot(-2)-3\cdot1}{-19},\frac{2\cdot1-(-1)\cdot5}{-19}}
=\bra{\frac{1}{19},-\frac{7}{19}}
\end{align*}
となる.
一般に,$x$, $y$の連立1次方程式
\begin{align*}\begin{cases}ax+by=p\\cx+dy=q\end{cases}\end{align*}
の解が一意なら,係数行列を$A$とするとクラメールの公式から
\begin{align*}(x,y)=\bra{\frac{1}{|A|}\vmat{p&b\\q&d},\frac{1}{|A|}\vmat{a&p\\c&q}}\end{align*}
となりますね.
具体例2(未知数が3つの連立1次方程式)
$a,b,c\in\R$は$a+b+c\neq0$を満たし,少なくとも1つは他と異なるとする.このとき,$x$, $y$, $z$の連立1次方程式
\begin{align*}\begin{cases}ax+by+cz=1\\bx+cy+az=0\\cx+ay+bz=0\end{cases}\end{align*}
を解け.
この問題も加減法(掃き出し法)によっても解けますが,係数が全て文字なので少し面倒です.
方程式が3本,未知数も3個で,係数行列が正則行列であることが分かるのでクラメールの公式が使えます.
係数行列を$A$とする.$A$の行列式は
\begin{align*}|A|&=\vmat{a&b&c\\b&c&a\\c&a&b}=-a^3-b^3-c^3+3abc
\\&=-\frac{1}{2}(a+b+c)\brb{(a-b)^2+(b-c)^2+(c-a)^2}\end{align*}
である.$a$, $b$, $c$の仮定から$|A|\neq0$(すなわち$A$は正則)だから,クラメールの公式を適用できて,解は
\begin{align*}(x,y,z)&=\bra{\frac{1}{|A|}\vmat{1&b&c\\0&c&a\\0&a&b},\frac{1}{|A|}\vmat{a&1&c\\b&0&a\\c&0&b},\frac{1}{|A|}\vmat{a&b&1\\b&c&0\\c&a&0}}
\\&=\bra{\frac{bc-a^2}{-a^3-b^3-c^3+3abc},\frac{ca-b^2}{-a^3-b^3-c^3+3abc},\frac{ab-c^2}{-a^3-b^3-c^3+3abc}}
\\&=\bra{\frac{a^2-bc}{a^3+b^3+c^3-3abc},\frac{b^2-ca}{a^3+b^3+c^3-3abc},\frac{c^2-ab}{a^3+b^3+c^3-3abc}}\end{align*}
となる.
参考文献
以下は参考文献です.
手を動かしてまなぶ 線形代数
[藤岡敦 著/裳華房]
線形代数の入門書で,説明も非常に丁寧なので初学者にも読み進めやすい教科書です.
数学で初めて出会った概念で詰まった時には,具体例を考えることで理解できるようになることはよくあります.
特に線形代数は高校数学で扱ってきた数学よりも抽象度がやや増すので,いきなり抽象的に理解するよりも「具体例を理解→抽象化」という学び方が効果的です.
本書は具体例と例題が豊富で,実際に手を動かしながらイメージを掴んで抽象的に理解することを目指しています.
また,続巻も発行されていますが,この第1巻だけでも正方行列の対角化(固有値・固有ベクトル)まで学ぶことができます.
線型代数入門
[齋藤正彦 著/東京大学出版会]
線形代数の教科書として半世紀に渡って売れ続けている超ロングセラーの教科書です.
発刊されてから本書の内容の流れが線形代数の教科書のスタンダードとなったほど,日本の線形代数の指導にインパクトを与えた名著です.
その証拠に,著者の齋藤正彦氏は本書で日本数学会出版賞を受賞しています.
「線形代数をとりあえず使えるようにするための教科書」ではなく「線形代数を理解するための教科書」のため,論理的に非常に詳しく書かれているのが特徴です.
また,テキストのレベルとしては少なくとも理論系(特に数学系)の学部生であれば,確実に理解しておきたい程度のものとなっています.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの教科書|線型代数入門(齋藤正彦著,東京大学出版会)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.

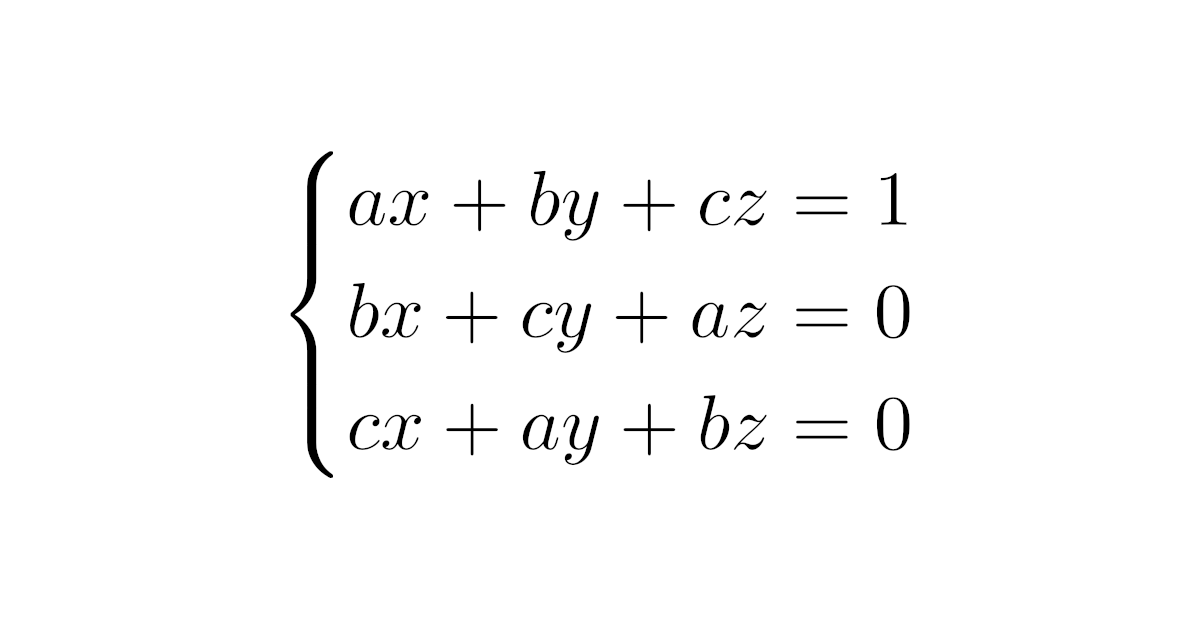


コメント