正方行列が正則であるための４つの必要十分条件を整理する

$n$次正方行列$A$が正則行列であるとは

\begin{align*}AB=BA=I_n\end{align*}

となる$n$次正方行列$B$が存在することをいいます．また，このとき$B$を$A$の逆行列といって$A^{-1}$と表すのでした．

正則行列はさまざまな「よい性質」をもち頻繁に現れるため，正方行列が正則かどうかの判定ができることは大切で，正方行列が正則であるためのよく用いる必要十分条件として次の定理はぜひ当たり前にしておきたい条件です．

$n$次正方行列$A=[\m{a}_1,\dots,\m{a}_n]$に対して，次の条件は同値である．

$A$は正則行列
$A$のランクは$n$：$\rank{A}=n$
連立１次方程式$A\m{x}=\m{0}$の解は自明解$\m{x}=\m{0}$のみ
$\m{a}_1,\dots,\m{a}_n$は線形独立
$A$の行列式は０でない：$\det{A}\neq0$

以下，この記事の行列の成分，ベクトルの成分，スカラーは全て実数であるとします．

この記事では

ランクによる必要十分条件
線形独立性による必要十分条件
連立１次方程式による必要十分条件
行列式による必要十分条件

を順に解説します．

ランクによる必要十分条件
線形独立性による必要十分条件
連立１次方程式による必要十分条件
行列式による必要十分条件

ランクによる必要十分条件

次の正方行列が正則行列であるためのランクによる必要十分条件を解説します．

$n$次正方行列$A$に対して，$A$が正則行列であることと，$\rank{A}=n$は同値である．

簡約行列に行基本変形したときの主成分の個数がランク

行列のランクの定義を確認しておきましょう．

行列$A$に行基本変形を施して簡約行列$B$になったとき，$B$の主成分の個数を$A$のランク（階数，rank）といい，

\begin{align*}\operatorname{rank}{A},\quad\operatorname{rk}{A}\end{align*}

などと表す．

階段行列の主成分が全て１であり，主成分が存在する列の主成分以外の成分が全て０である

\begin{align*}\bmat{\color{blue}\m{1}&\color{blue}\dots&\color{blue}*&\color{blue}0&\color{blue}\dots&\color{blue}*&\color{blue}0&\color{blue}\dots&\color{blue}*&\color{blue}*
\\0&\dots&0&\color{blue}\m{1}&\color{blue}\dots&\color{blue}*&\color{blue}0&\color{blue}\dots&\color{blue}*&\color{blue}*
\\0&\dots&0&0&\dots&0&\color{blue}\m{1}&\color{blue}\dots&\color{blue}*&\color{blue}*
\\\vdots&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots}\end{align*}

のような行列を簡約行列というのでした（太字になっている部分が主成分）．例えば，行列$\bmat{2&3&-2\\2&-2&8\\-3&0&-6}$は行基本変形により

\begin{align*}\bmat{2&3&-2\\2&-2&8\\-3&0&-6}
&\to\bmat{2&3&-2\\1&-1&4\\-3&0&-6}
\to\bmat{2&3&-2\\1&-1&4\\-1&0&-2}
\\&\to\bmat{1&-1&4\\2&3&-2\\-1&0&-2}
\to\bmat{1&-1&4\\0&5&-10\\0&-1&2}
\\&\to\bmat{1&-1&4\\0&1&-2\\0&-1&2}
\to\bmat{1&0&2\\0&1&-2\\0&0&0}\end{align*}

と簡約行列に変形でき，$\operatorname{rank}{A}=2$と分かります．

簡約行列まで変形する行基本変形の方法は様々なルートがありますが，どのように行基本変形しても同じ簡約行列になることが証明できます．

定義するだけであれば「行基本変形してできる階段行列の主成分の個数をランクという」で十分ですが，このあとの議論で簡約行列の一意性を用いるので簡約行列の主成分の個数を定義に用いています．

ある正則行列をかけることで基本変形が引き起こされる

また，基本変形は正則行列をかけることで引き起こすことができるという次の命題を思い出しておきましょう．

［行基本変形と正則行列］$m\times n$行列の行基本変形は$m$次正則行列を左からかけることで引き起こされる．

例えば，３×２行列$A=\bmat{1&2\\3&4\\5&6}$と，３次正方行列

\begin{align*}P_1=\bmat{1&0&0\\0&0&1\\0&1&0},\quad
P_2=\bmat{1&0&0\\0&2&0\\0&0&1},\quad
P_3=\bmat{1&0&0\\0&1&-2\\0&0&1}\end{align*}

を考えます．このとき，単純に計算して

\begin{align*}P_1A=\bmat{1&2\\5&6\\3&4},\quad
P_2A=\bmat{1&2\\2\cdot3&2\cdot4\\5&6},\quad
P_3A=\bmat{1&2\\3-2\cdot5&4-2\cdot6\\5&6}\end{align*}

となり，もとの$A$を見比べてみると行基本変形が起こっていることが分かります．

基本となる３種の行基本変形が正則行列を左からかけることで引き起こせるので，何回も正則行列をかければどんな行基本変形も引き起こすことができますね．

正則であるためのランクによる必要十分条件の証明

（再掲）$n$次正方行列$A$に対して，$A$が正則行列であることと，$\rank{A}=n$は同値である．

$A$に行基本変形を施して簡約行列$B$になるとする．このとき，命題［行基本変形と正則行列］より$PA=B$を満たすある$n$次正則行列$P$が存在する．

$A$が正則なら$\rank{A}=n$の証明

$A$は正則行列とする．一般に正則行列の積は正則行列なので$PA$は正則行列だから，$PA$と等しい$B$も正則行列である．

ここで，もし$\rank{A}<n$なら簡約行列$B$の主成分の個数は$n$個未満なので$B$の第$n$行の成分は全て０であるが，これは$B$が正則であることに矛盾するから$\rank{A}=n$が従う．

$\rank{A}=n$なら$A$は正則の証明

$\rank{A}=n$とする．ランクの定義より，$A$に行基本変形を施してできる簡約行列$B$の主成分の個数は$n$個である．

$B$は$n$次正方行列だから$B=I$であることが分かり，$PA=I$が成り立つ．

よって，両辺に左から$P^{-1}$をかけて$A=P^{-1}$となり，$P^{-1}$は正則行列だから$A$も正則行列である．

線形独立性による必要十分条件

次の正方行列が正則行列であるための線形独立性による必要十分条件を考えます．

$n$次正方行列$A=[\m{a}_1,\m{a}_2,\dots,\m{a}_n]$に対して，$A$が正則行列であることと，$\m{a}_1,\m{a}_2,\dots,\m{a}_n$が線形独立であることは同値である．

線形独立性とはベクトルたちがバラバラの方向を向いていること

$\m{a}_1,\m{a}_2,\dots,\m{a}_r\in\R^n$が線形独立であるとは

\begin{align*}k_1\m{a}_1+k_2\m{a}_2+\dots+k_r\m{a}_r=\m{0}\end{align*}

を満たす$k_1,k_2,\dots,k_r\in\R$が$k_1=k_2=\dots=k_r=0$以外にないことをいう．

$\m{a}_1,\m{a}_2,\dots,\m{a}_r\in\R^n$が線形独立であれば，どの$\m{a}_s$も

\begin{align*}\m{a}_s=k_1\m{a}_1+\dots+k_{s-1}\m{a}_{s-1}+k_{s+1}\m{a}_{s+1}+\dots+k_{r}\m{a}_{r}\end{align*}

と表すことができませんから，どの$\m{a}_s$も他のベクトルたちの張る空間上にないということになります．

つまり，直感的には線形独立なベクトルたちは本質的にバラバラの方向を向いていると捉えることができます．

行列をなす列ベクトルの線形独立性と行基本変形

２つの行列が行基本変形で移り合うとき，２つの行列をなす列ベクトルたちの線形関係は保たれます．

［行基本変形と線形関係］行列$A=[\m{a}_1,\m{a}_2,\dots,\m{a}_r]$に行基本変形を施して行列$B=[\m{b}_1,\m{b}_2,\dots,\m{b}_r]$になったとする．このとき，$k_1,k_2,\dots,k_r\in\R$に対して，次は同値である．

$k_1\m{a}_1+k_2\m{a}_2+\dots+k_r\m{a}_r=\m{0}$が成り立つ
$k_1\m{b}_1+k_2\m{b}_2+\dots+k_r\m{b}_r=\m{0}$が成り立つ

行列$A$に行基本変形を施して$B$になるので，$PA=B$を満たす正則行列$P$が存在する．よって，

\begin{align*}[P\m{a}_1,P\m{a}_2,\dots,P\m{a}_r]=[\m{b}_1,\m{b}_2,\dots,\m{b}_r]\end{align*}

となり，任意の$k\in\{1,2,\dots,r\}$に対して$P\m{a}_k=\m{b}_k$が成り立つ．よって，$k_1,k_2,\dots,k_r\in\R$に対して

\begin{align*}&k_1\m{a}_1+k_2\m{a}_2+\dots+k_r\m{a}_r=\m{0}
\\&\iff k_1P\m{a}_1+k_2P\m{a}_2+\dots+k_rP\m{a}_r=\m{0}
\\&\iff k_1\m{b}_1+k_2\m{b}_2+\dots+k_r\m{b}_r=\m{0}\end{align*}

が成り立つ．

行列のランクは行列をなす列ベクトルの線形独立なものの最大個数に等しい

次の補題は当たり前にしておきましょう．

［主成分の個数］簡約行列$B=[\m{b}_1,\m{b}_2,\dots,\m{b}_r]$の主成分の個数と，$\m{b}_1,\m{b}_2,\dots,\m{b}_r$のうち線形独立なものの最大個数は等しい．

簡約行列$B$の主成分はちょうど$t$個であるとし，$B$の第$n_1,n_2,\dots,n_t$列に主成分が存在するとする（$n_1<n_2<\dots<n_t$）と，$\m{b}_{n_s}$は第$n_s$成分が１で他の成分が０の列ベクトルである：

\begin{align*}\m{b}_{n_1}=\sbmat{1\\0\\\vdots\\0\\0\\\vdots},\quad\m{b}_{n_2}=\sbmat{0\\1\\\vdots\\0\\0\\\vdots},\quad\dots,\quad\m{b}_{n_t}=\sbmat{0\\0\\\vdots\\1\\0\\\vdots}.\end{align*}

また，第$n_1,n_2,\dots,n_t$列以外の列の第$(t+1)$行以降の成分は全て０である．

よって，$\m{b}_{n_1},\m{b}_{n_2},\dots,\m{b}_{n_t}$は線形独立で，他の列は全て$\m{b}_{n_1},\m{b}_{n_2},\dots,\m{b}_{n_t}$の線形結合で表せるから，$\m{b}_1,\m{b}_2,\dots,\m{b}_r$のうち線形独立なものは最大で$t$個である．

この補題を用いると，行列のランクと列ベクトルの線形独立性に次の密接な関係があることを示すことができます．

［ランクと線形独立性］行列$A=[\m{a}_1,\m{a}_2,\dots,\m{a}_r]$に対して，次は同値である．

$\m{a}_1,\m{a}_2,\dots,\m{a}_r$のうち線形独立なものは最大で$s$個
$\rank{A}=s$

行列$A$に行基本変形を施して，簡約行列$B=[\m{b}_1,\m{b}_2,\dots,\m{b}_r]$になるとする．

命題［行基本変形と線形関係］より，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$の線形関係と$\m{b}_1,\m{b}_2,\dots,\m{b}_r$の線形関係は一致するから，

$\m{a}_1,\m{a}_2,\dots,\m{a}_r$のうち線形独立なものが最大で$s$個
$\m{b}_1,\m{b}_2,\dots,\m{b}_r$のうち線形独立なものは最大で$s$個

は同値である．$B$が簡約行列だから補題［主成分の個数］と併せると，これは$B$の主成分の個数がちょうど$s$個であることと同値で，ランクの定義からさらに$\rank{A}=s$と同値である．

正則であるための線形独立性による必要十分条件の証明

ランクによる必要十分条件と，いま示した命題［ランクと線形独立性］が理解できていれば，線形独立性による必要十分条件はほとんど当たり前です．

（再掲）$n$次正方行列$A=[\m{a}_1,\m{a}_2,\dots,\m{a}_n]$に対して，$A$が正則行列であることと，$\m{a}_1,\m{a}_2,\dots,\m{a}_n$が線形独立であることは同値である．

正則であるためのランクによる必要十分条件より，$A$が正則行列であることと$\rank{A}=n$は同値である．

命題［ランクと線形独立性］より，$\m{a}_1,\m{a}_2,\dots,\m{a}_n$のうち線形独立なものは最大で$n$個であることと同値で，これは$\m{a}_1,\m{a}_2,\dots,\m{a}_n$が線形独立であることに他ならない．

連立１次方程式による必要十分条件

次の正方行列が正則行列であるための連立１次方程式による必要十分条件を考えます．

$n$次正方行列$A$に対して，$A$が正則行列であることと，連立１次方程式$A\m{x}=\m{0}$の解が自明解のみであることは同値である．

連立１次方程式を行列とベクトルで表す

例えば，連立１次方程式$\begin{cases}x+2y+3z=6\\4x+5y+6z=9\\7x+8y+9z=12\end{cases}$は

\begin{align*}\bmat{1&2&3\\4&5&6\\7&8&9}\bmat{x\\y\\z}=\bmat{6\\9\\12}\end{align*}

と行列とベクトルの積に書き換えられますね．

このように，一般に連立１次方程式は係数行列$A$と定数の列ベクトル$\m{c}$によって$A\m{x}=\m{c}$の形で表すことができます．$\m{x}$は未知数の列ベクトルですね．

とくに連立１次方程式$A\m{x}=\m{c}$の定数の列ベクトル$\m{c}$が零ベクトル$\m{0}$のとき，この連立１次方程式$A\m{x}=\m{0}$を斉次（または同次）であるといいます．

斉次連立１次方程式$A\m{x}=\m{0}$の自明解

そもそも方程式の解とは，方程式に代入して等式が成り立つようなものをいうのでした．

斉次連立１次方程式$A\m{x}=\m{0}$に対して，$A\m{0}=\m{0}$は必ず成り立つので零ベクトル$\m{0}$を解にもち，この解を自明解といいます．

斉次連立１次方程式$A\m{x}=\m{0}$の解$\m{x}=\m{0}$を自明解という．

斉次連立１次方程式$A\m{x}=\m{0}$が自明解以外の解を持つかどうかは係数行列$A$によるわけですが，$A\m{x}=\m{0}$が自明解のみであるための必要十分条件が$A$が正則行列であるというのが上の定理ですね．

連立１次方程式を線形結合の立場から考える

連立１次方程式と列ベクトルの線形結合について，次の密接な関係があります．

［解の一意性］$n$行の行列$A=[\m{a}_1,\m{a}_2,\dots,\m{a}_r]$と$\m{c}\in\R^n$に対して，次は同値である．

連立１次方程式$A\m{x}=\m{c}$の解は一意に存在
$\m{a}_1,\m{a}_2,\dots,\m{a}_r$の線形結合で$\m{c}$を一意に表せる

$\m{x}=\sbmat{x_1\\x_2\\\vdots\\x_r}$とすると，連立１次方程式$A\m{x}=\m{c}$は

\begin{align*}x_1\m{a}_1+x_2\m{a}_2+\dots+x_r\m{a}_r=\m{c}\quad\dots(*)\end{align*}

と書き換えられる．よって，連立１次方程式$A\m{x}=\m{c}$が解をもつことと，$(*)$を満たす$x_1,x_2,\dots,x_r$が存在することは同値である．すなわち，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$の線形結合で$\m{c}$が表せることと同値である．

連立１次方程式$A\m{x}=\m{c}$は「$A$をなす列ベクトル$\m{a}_1,\m{a}_2,\dots,\m{a}_r$の線形結合で$\m{c}$を表す問題」と捉え直すことができるわけですね．

正則であるための連立１次方程式による必要十分条件の証明

線形独立性による必要十分条件と，連立１次方程式$A\m{x}=\m{0}$を「$A$の列ベクトルの線形結合で$\m{0}$を表す問題」と捉えることで，連立１次方程式による必要十分条件は次のように証明できます．

（再掲）$n$次正方行列$A$に対して，$A$が正則行列であることと，連立１次方程式$A\m{x}=\m{0}$の解が自明解のみであることは同値である．

$A=[\m{a}_1,\m{a}_2,\dots,\m{a}_n]$とおく．

正則であるための線形独立性による必要十分条件より，$A$が正則行列であることと$\m{a}_1,\m{a}_2,\dots,\m{a}_n$が線形独立であることは同値である．

線形独立性の定義より，これは$\m{a}_1,\m{a}_2,\dots,\m{a}_r$の線形結合で$\m{0}$を一意に表せることに他ならない．

よって，命題［解の一意性］と併せて，斉次連立１次方程式$A\m{x}=\m{0}$の解が一意に存在することと同値である．

行列式による必要十分条件

次の正方行列が正則行列であるための行列式による必要十分条件を考えます．

$n$次正方行列$A$に対して，$A$が正則行列であることと，$\det{A}\neq0$であることは同値である．

$n$次正方行列の行列式は立体の$n$次元体積を表す

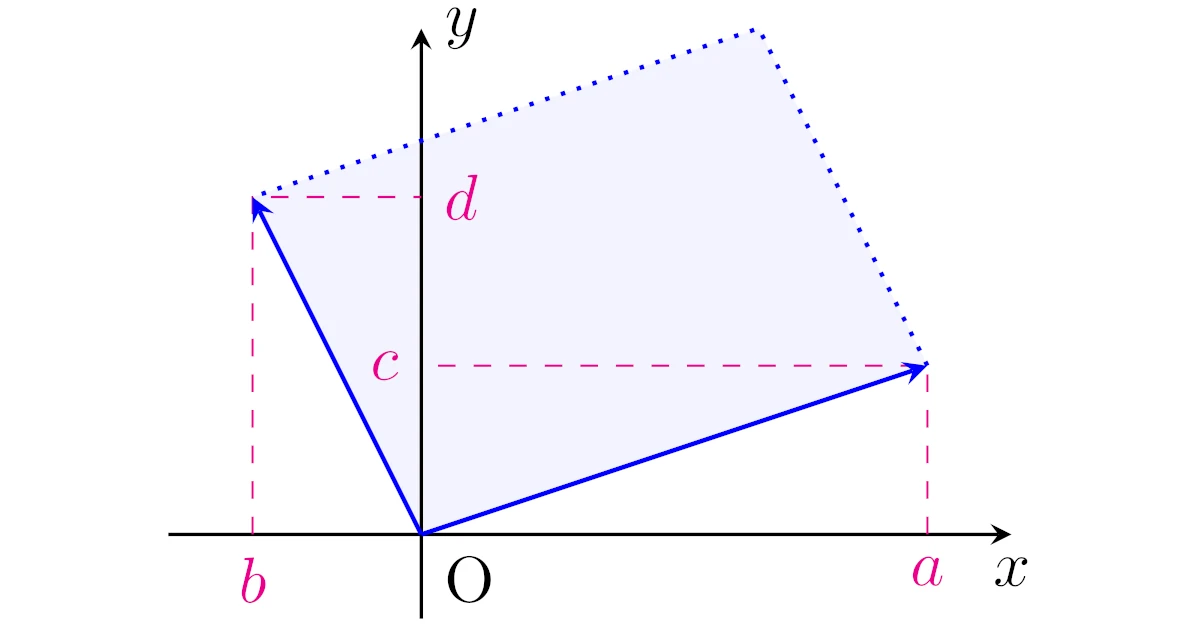
２次正方行列$\bmat{a&b\\c&d}$の行列式

\begin{align*}\det\bmat{a&b\\c&d}=ad-bc\end{align*}

の絶対値$|ad-bc|$は，（高校数学のベクトルの分野で学ぶように）列ベクトル$\bmat{a\\c}$, $\bmat{b\\d}$がなす$xy$平面上の平行四辺形の面積を表します（$\m{a}$と$\m{b}$が平行なら平行四辺形は「潰れて」面積は０と考えます）．

$ベクトル(a,c),(b,d)がなす平行四辺形$

ベクトルの三角形の面積公式を２倍すれば平行四辺形の面積$|ad-bc|$が得られる

より詳しくは，いずれも零ベクトルでない$\m{a}:=\bmat{a\\c}$, $\m{b}:=\bmat{b\\d}$を$xy$平面上に図示したとき

$\m{a}$を正方向へ180°未満回転させて$\m{b}$と同じ向きになるなら$ad-bc>0$
$\m{a}$を負方向へ180°未満回転させて$\m{b}$と同じ向きになるなら$ad-bc<0$

となります．

$ベクトル(a,c),(b,d)の2種類の位置関係による平行四辺形$

ベクトル$\m{a}$, $\m{b}$の位置関係で行列式の正負が決まる

２次正方行列では２次列ベクトルのなす平行四辺形の面積でしたが，３次正方行列$[\m{a},\m{b},\m{c}]$の行列式の絶対値$|\det[\m{a},\m{b},\m{c}]|$は$\m{a},\m{b},\m{c}$がなす$xyz$空間上の平行六面体の体積を表します．

$ベクトルa,b,cがなす平行六面体$

平行六面体は２次元の平行四辺形の３次元ver.と捉えられる

一般に$n$次正方行列$[\m{a}_1,\m{a}_2,\dots,\m{a}_n]$の行列式の絶対値は$\m{a}_1,\m{a}_2,\dots,\m{a}_n$がなす$n$次元直交座標上の「$n$次元平行多胞体」の$n$次元体積を表すと捉えることができます．

$n$次元平行多胞体とは２次元の平行四辺形，３次元の平行六面体の$n$次元に拡張したもので，$\m{p}\in\R^n$と線形独立な$\m{a}_1,\m{a}_2,\dots,\m{a}_n\in\R^n$によって$\set{\m{p}+\sum_{k=1}^{n}\theta_k\m{a}_k}{0\le\theta_k\le1;k=1,2,\dots,n}$で表される図形です．