「相関係数」は相関の強さを表す｜定義と考え方を解説

たとえば，２種類の対応するデータ

勉強時間
テストの点数

を考えたとき，勉強時間が長いほどテストの点数が高くなる傾向がありそうです．

このように，「一方のデータの値が大きいときに他方のデータの値も大きいこと」を正の相関があるといい，逆に「一方のデータの値が大きいときに他方のデータの値は小さいこと」を負の相関があるというのでした．

これらについて前回の記事では共分散を考えることで相関の正負が判断できることを説明しましたが，共分散だけではどれくらい強い相関があるのかまでは分かりません．

そこで，相関の強さまで測ることのできる統計量が欲しいわけですが，その統計量がこの記事で説明する相関係数です．

この記事では

相関の強さ
相関係数の定義・具体例
相関係数と相関の強さの関係

を説明します．

「統計学」の一連の記事

基本の統計量

回帰直線

推定
1. e1 不偏分散ってなに？｜不偏推定量を考え方から理解する
2. e2 尤度関数の考え方｜データから分布を推定する最尤推定法の例

相関の強さ
1. 相関が強いとは？
2. 無相関
相関係数
1. 相関係数の定義
2. 相関係数の具体例
相関係数と相関の強さの関係
1. 相関係数の基本性質
2. 相関係数$\rho$が相関の強さを表す理由
回帰直線
参考文献
1. 改訂版統計検定２級対応統計学基礎

相関の強さ

相関係数を説明する前に，相関の強さについて説明します．

相関が強いとは？

テストを受けた８人の生徒について

勉強時間$x$
テストの点数$y$

のデータをとると，以下の散布図として表せたとします．

この図を見ると，データはだいたい右上がりになっている，つまり正の相関があるということが見てとれます．

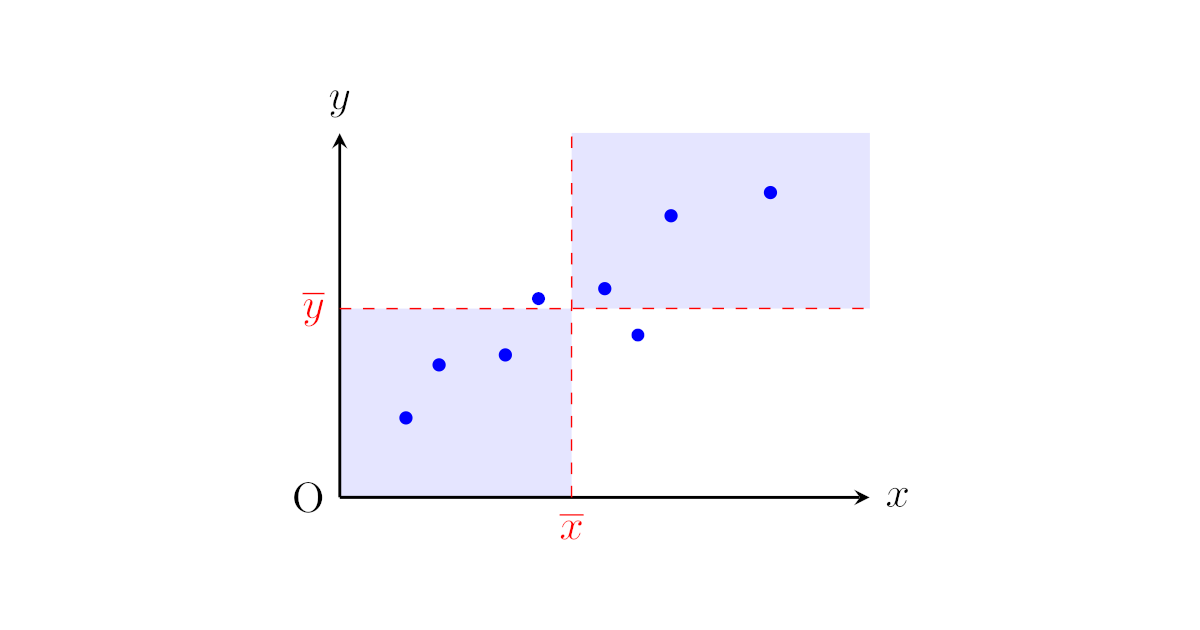
また，別の対応する２種類のデータ$(x,y)$の散布図が以下のようになったとします．

この散布図は先ほどの散布図よりもデータの配置が直線に近くなっています．

このように，２種類の対応するデータ$(x,y)$を散布図に表したとき，点の分布が直線に近いほど相関が強いといいます．

[正の相関が強い]

Rendered by QuickLaTeX.com

[負の相関が強い]

Rendered by QuickLaTeX.com

よって，

データ$(x_i,y_i)$の点が正の傾きの直線上に乗っているときが最強の正の相関
データ$(x_i,y_i)$の点が負の傾きの直線上に乗っているときが最強の負の相関

というわけですね．

無相関

正の相関も負の相関もないことを無相関といいます

正確には後に説明する相関係数が$0$であることをいいます．

要するに，点がバラバラな散布図を持つようなデータ$(x,y)$が無相関ですね．

ただし，注意として

$x$と$y$が無相関であること
$x$と$y$が無関係であること

は別の話です．

たとえば，以下のような散布図を持つデータ$(x,y)$は正の相関も負の相関もないため無相関です．

しかし，この$x$と$y$には「点$(x,y)$が円周上にある」という「関係」はありますね．

このように，２種類のデータ$(x,y)$が無相関であって，関係がないのとはまた別の話であることに注意してください．

相関係数

それでは，「相関の強さ」を表す相関係数の説明に移ります．

相関係数の定義

説明は後回しにして，先に相関係数の定義を書いてしまいます．相関係数を考えるには

$x$と$y$の共分散$C_{xy}$
$x$の標準偏差$\sigma_x$
$y$の標準偏差$\sigma_y$

が必要です．

データの分散・標準偏差｜統計学で「ばらつき」を表す方法

年収のデータをとったとき，高所得者が多いと平均値が大きく吊り上げられ，平均年収がデータの実態にそぐわなくなることがあります．このように，データのばらつきが大きいとき，統計学では「分散（標準偏差）が大きい」といいます．

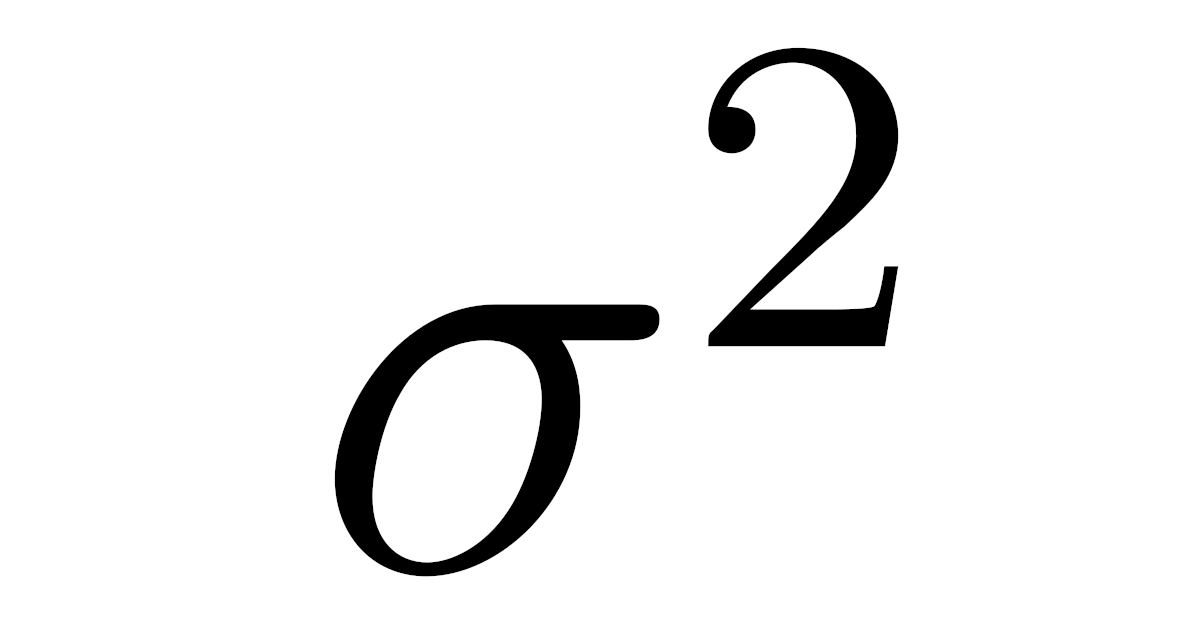
[相関係数]　２種類のデータ$x_1,x_2,\dots,x_n$と$,y_1,y_2,\dots,y_n$に対して，それぞれの標準偏差を$\sigma_x(\neq0)$, $\sigma_y(\neq0)$とし，これらの共分散を$C_{xy}$とする．このとき，このデータの組$(x,y)$の相関係数 (correlation coefficient)$\rho_{xy}$を

$\begin{align*}\rho_{xy}=\frac{C_{xy}}{\sigma_x\sigma_y}\end{align*}$

で定義する．

また，相関係数が$0$であるとき，２種類のデータ$x_1,x_2,\dots,x_n$と$,y_1,y_2,\dots,y_n$は無相関であるといいます．

相関係数の定義から

$\rho_{xy}=0$
$C_{xy}=0$

は同値なので，無相関であることを示すには$C_{xy}=0$を示せばよいことはよく用いられます．

相関係数の具体例

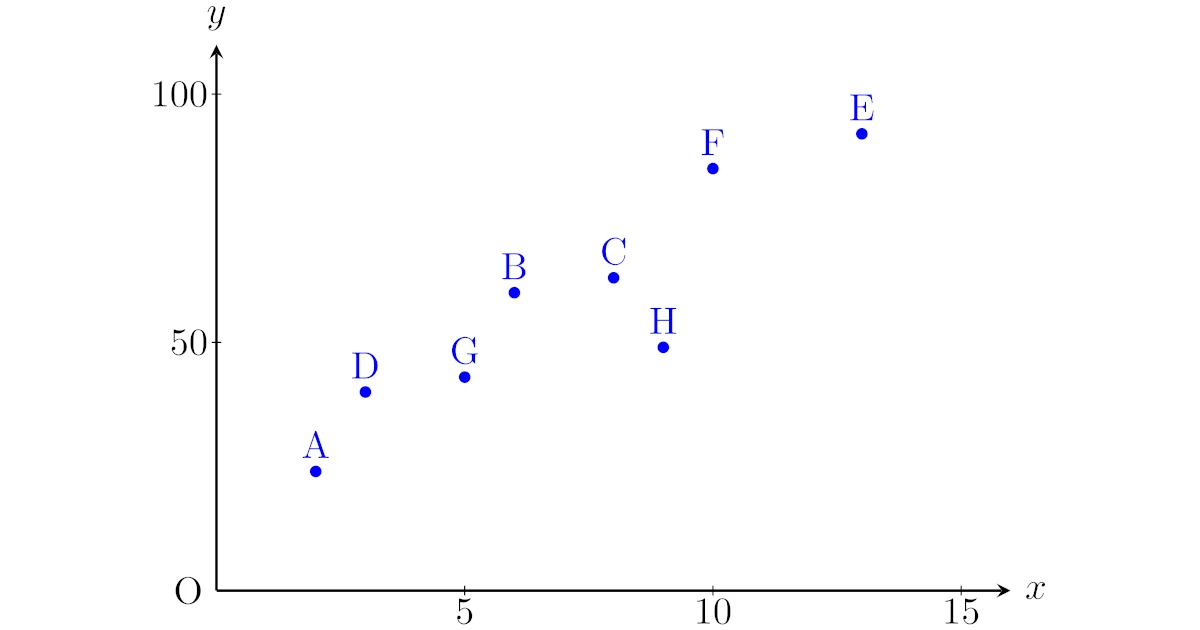
あるテストを受けた８人の生徒について

勉強時間$x$
テストの点数$y$

が以下の表のようになったとしましょう．

勉強時間$x$とテストの点数$y$
人	A	B	C	D	E	F	G	H
勉強時間$x$	2	6	8	3	13	10	5	9
テストの点数$y$	24	60	63	40	92	85	43	49

このデータは前回の記事で扱ったデータと同じもので，共分散$C_{xy}$が$C_{xy}=\frac{271}{4}=67.75$となることは前回の記事で実際に計算しました．

統計学の基礎３｜「共分散」は「相関」の正負を表す統計量

「勉強時間」が長いほど「テストの得点」は高いことが予想できますが，このように一方が大きいときに他方も大きい傾向があることを「正の相関」があるといいます．逆に，一方が大きいときに他方が小さい傾向があることを「負の相関」があるといいます．

あとは$x$の標準偏差$\sigma_x$，$y$の標準偏差$\sigma_y$が必要ですね．

標準偏差については以下の記事で説明しています．

データの分散・標準偏差｜統計学で「ばらつき」を表す方法

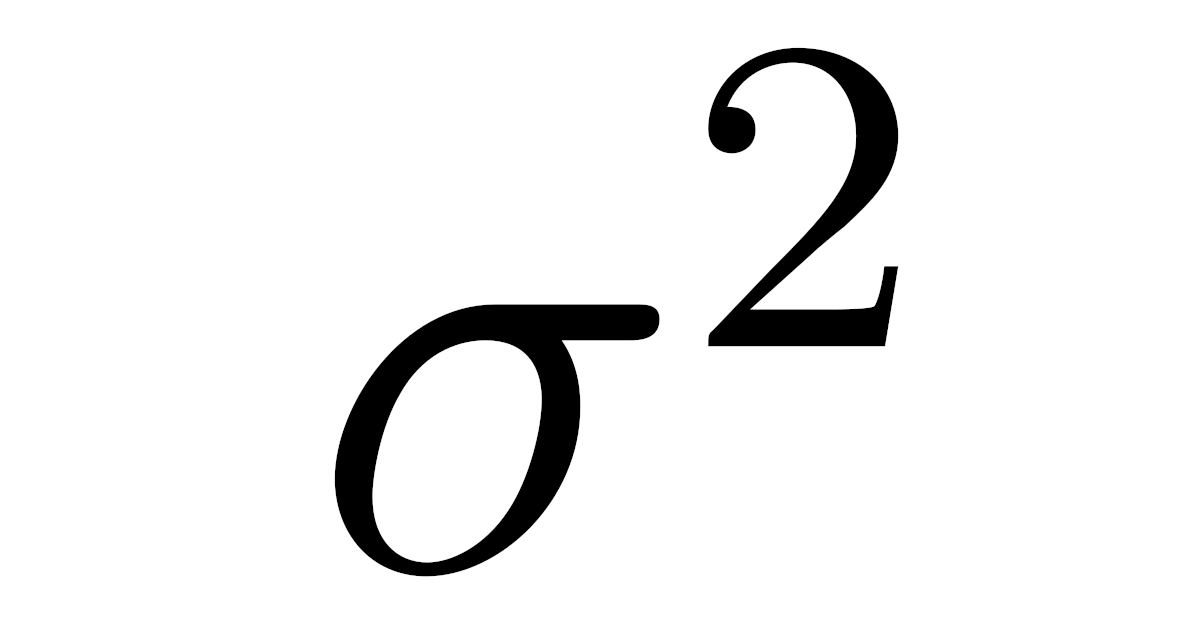
$x$の平均，$y$の平均はそれぞれ

$\begin{align*}&\overline{x}=\frac{2+6+8+3+13+10+5+9}{8}=7, \\&\overline{y}=\frac{24+60+63+40+92+85+43+49}{8}=57\end{align*}$

なので，$x$の標準偏差$\sigma_x$，$y$の標準偏差$\sigma_y$はそれぞれ

$\begin{align*}\sigma_x =&\sqrt{\begin{aligned}\frac{1}{8}&\{(2-7)^2+(6-7)^2+(8-7)^2+(3-7)^2\\ &\quad+(13-7)^2+(10-7)^2+(5-7)^2+(9-7)^2\}\end{aligned}} \\=&\sqrt{\frac{25+1+1+16+36+9+4+4}{8}} \\=&\sqrt{12} =2\sqrt{3}, \\\sigma_y =&\sqrt{\begin{aligned}\frac{1}{8}&\{(24-57)^2+(60-57)^2+(63-57)^2+(40-57)^2\\ &\quad+(92-57)^2+(85-57)^2+(43-57)^2+(49-57)^2\}\end{aligned}} \\=&\sqrt{\frac{2089+9+36+9+1225+784+196+64}{8}} \\=&\sqrt{\frac{1103}{2}}\end{align*}$

となります．よって，相関係数$\rho_{xy}$は

$\begin{align*}\rho_{xy} =\frac{67.75}{2\sqrt{3}\cdot\sqrt{\frac{1103}{2}}} =\frac{67.75}{\sqrt{6618}} \approx0.83281\end{align*}$

となりますね．

相関係数と相関の強さの関係

さて，今求めた相関係数$\rho_{xy}\approx0.83281$からどのように相関の強さが分かるでしょうか？

相関係数の基本性質

相関係数について，実は次が成り立ちます．

相関係数$\rho$は$-1\le\rho\le1$を満たす．

データの数がどれだけ多かろうが，必ず相関係数は$-1$から$1$の間の値になります．

また，このあとで説明するように，相関係数$\rho$は

$1$に近いほど正の相関が強い
$0$に近いほど無相関に近い
$-1$に近いほど正の相関が強い

ということを表します．もう少し詳しく分けると，相関の強さの目安は

$-1\le\rho\le-0.9$：かなり強い負の相関
$-0.9<\rho\le-0.7$：強めの負の相関
$-0.7<\rho\le-0.5$：負の相関
$-0.5<\rho\le-0.3$：弱めの負の相関
$-0.3<\rho<0.3$：無相関
$0.3\le\rho<0.5$：弱めの正の相関
$0.5\le\rho<0.7$：正の相関
$0.7\le\rho<0.9$：強めの正の相関
$0.9\le\rho\le1$：かなり強い正の相関

とされることが多いです．

そのため，先ほど求めた相関係数$\rho_{xy}\approx0.83281$は「強めの正の相関である」ということになりますね．

相関係数$\rho$が相関の強さを表す理由

２つの対応するデータ$x_1,x_2,\dots,x_n$と$y_1,y_2,\dots,y_n$について，散布図の点$(x_i,y_i)$たちが直線上に並んでいる状態が最も相関が強いのでした．

このことは，２つの$n$次元ベクトル

$\begin{align*}\m{x}:=\bmat{x_1-\overline{x}\\x_2-\overline{x}\\\vdots\\x_n-\overline{x}},\quad \m{y}:=\bmat{y_1-\overline{y}\\y_2-\overline{y}\\\vdots\\y_n-\overline{y}}\end{align*}$

が平行であることに他なりません．

さらに詳しく言えば

$\m{x}$と$\m{y}$が同じ方向を向いているとき，相関係数は$1$
$\m{x}$と$\m{y}$が逆方向を向いているとき，相関係数は$-1$

となります．

さて，ここで次のコーシー-シュワルツ(Cauchy-Schwarz)の不等式を確認しておきましょう．

[コーシー-シュワルツの不等式]　実数成分ベクトル$\m{x}$, $\m{y}$に対して

$\begin{align*}-|\m{x}||\m{y}|\le\m{x}\cdot\m{y}\le|\m{x}||\m{y}|\end{align*}$

が成り立つ．ただし，

$|\m{x}|$は$\m{x}$の長さ
$\m{x}\cdot\m{y}$は$\m{x}$と$\m{y}$の標準内積

である．

コーシー-シュワルツの不等式について，一般に

２つのベクトル$\m{x}$と$\m{y}$が同じ向きに近いほど，内積$\m{x}\cdot\m{y}$は$|\m{x}||\m{y}|$に近い
２つのベクトル$\m{x}$と$\m{y}$が逆向きに近いほど，内積$\m{x}\cdot\m{y}$は$-|\m{x}||\m{y}|$に近い

ということが言えます．

さて，ここでコーシー-シュワルツの不等式を$|\m{x}||\m{y}|$で割ると

$\begin{align*}-1\le\frac{\m{x}\cdot\m{y}}{|\m{x}||\m{y}|}\le1\end{align*}$

となるので，いま書いたことは

２つのベクトル$\m{x}$と$\m{y}$が同じ向きに近いほど，内積$\frac{\m{x}\cdot\m{y}}{|\m{x}||\m{y}|}$は$1$に近い
２つのベクトル$\m{x}$と$\m{y}$が逆向きに近いほど，内積$\frac{\m{x}\cdot\m{y}}{|\m{x}||\m{y}|}$は$-1$に近い

と言い換えることができます．

ここで，内積$\m{x}\cdot\m{y}$，長さ$|\m{x}|$，長さ$|\m{y}|$に

$\begin{align*}\m{x}:=\bmat{x_1-\overline{x}\\x_2-\overline{x}\\\vdots\\x_n-\overline{x}},\quad \m{y}:=\bmat{y_1-\overline{y}\\y_2-\overline{y}\\\vdots\\y_n-\overline{y}}\end{align*}$

を代入すると，

$\begin{align*}\m{x}\cdot\m{y}=&(x_1-\overline{x})(y_1-\overline{y})+\dots+(x_n-\overline{x})(y_n-\overline{y}), \\|\m{x}|=&\sqrt{(x_1-\overline{x})^2+\dots+(x_n-\overline{x})^2}, \\|\m{y}|=&\sqrt{(y_1-\overline{y})^2+\dots+(y_n-\overline{y})^2}\end{align*}$

となって，それぞれ$nC_{xy}$, $\sqrt{n}\sigma_x$, $\sqrt{n}\sigma_y$となっているので

$\begin{align*}\frac{\m{x}\cdot\m{y}}{|\m{x}||\m{y}|} =\frac{nC_{xy}}{\sqrt{n}\sigma_x\cdot\sqrt{n}\sigma_y} =\frac{C_{xy}}{\sigma_x\sigma_y}\end{align*}$