2023年度の東京大学 数理科学研究科の大学院入試問題の専門科目Bの解答の方針と解答例です.
問題は18題あり,選択して3題を解答します.試験時間は4時間です.この記事では,第9〜12問について解説しています.
ただし,公式に採点基準などは発表されていないため,本稿の解答が必ずしも正解になるとは限りません.ご注意ください.
また,十分注意して解答を作成していますが,論理の飛躍・誤りが残っている場合があります.
なお,最近の過去問は東京大学の数理科学研究科のホームページから入手できます.
第9問(関数解析)
閉区間$[0,1]$上の実数値$L^\infty$関数からなるバナッハ空間$L^\infty([0,1])$を$X$で表す.ただし,$[0,1]$上の測度としてはルベーグ測度を考えるものとする.
- 任意の$f\in X$に対し,次で定まる関数$Tf$は$[0,1]$上連続であることを示せ.\begin{align*}(Tf)(x)=\int_0^1 \frac{f(y)}{|x-y|^{1/2}}\,dy,\quad x\in[0,1].\end{align*}
- 線型作用素$T:X\to X$の作用素ノルム$\|T\|$を求めよ.
- $f\in X$が等式\begin{align*}\|Tf\|_\infty=\|T\|\|f\|_\infty\end{align*}を満たすならば,$f$は定数関数であることを示せ.
線形作用素$T$が(1)で連続(すなわち有界)であることを示し,(2)で$T$の作用素ノルムを求めます.
解答の方針とポイント
丁寧に基本を押さえていれば,(1)も(2)も定石通りに考えれば解けます.(3)は(2)までの計算を踏まえれば方針が見えます.
$L^p$平行移動連続性
関数$Tf$は$[0,1]$上連続であることを示すには,任意に$a\in[0,1]$をとり,$\lim\limits_{h\to0}Tf(a+h)=Tf(a)$を示せばよいですね.
\begin{align*}|Tf(a+h)-Tf(a)|\le\int_{[0,1]}\abs{\frac{f(y)}{|a+h-y|^{1/2}}-\frac{f(y)}{|a-y|^{1/2}}}\,dy\end{align*}
であり,被積分関数は0に収束するので全体としても0に収束しそうです.ここで,次の定理が使えます.
[$L^p$平行移動連続性]$p\ge1$とする.任意の$f\in L^p(\R)$に対して,
\begin{align*}\lim_{h\to0}\int_{\R}|f(x+h)-f(x)|\,dx=0\end{align*}
が成り立つ.
$\frac{f(y)}{|a-y|^{1/2}}\in L^1_y([0,1])$なので,$\R$へは0拡張すれば$L^1$平行移動連続性より$\lim\limits_{h\to0}|Tf(a+h)-Tf(a)|=0$が得られます.
極限と積分の順序交換を示すにはルベーグの収束定理を用いるのが常套手段ですが,$|\frac{f(y)}{|a+h-y|^{1/2}}-\frac{f(y)}{|a-y|^{1/2}}|\le g(y)$となる可積分関数$g$がとれないので,(1)をルベーグの収束定理を用いて解くのは難しいでしょう.
作用素ノルムの求め方
有界線形作用素$T:X\to Y$に対して,
\begin{align*}\|T\|=\sup_{f\in X\setminus\{0\}}\frac{\|Tf\|_Y}{\|f\|_X}\end{align*}
を$T$の作用素ノルムという.
作用素$T:X\to Y$の作用素ノルムについて,$\|T\|=C$であることは
- 定義域上の任意の$f\in X$に対して$\|Tf\|\le C\|f\|$を示す
- $\|Tf\|=C\|f\|$を満たす$f\in X$(もしくは$\frac{\|Tf_n\|}{\|f_n\|}\to C$を満たす$X$の列$\{f_n\}$)を具体的にとる
の2ステップで示すのが基本です.本問では
\begin{align*}|Tf(x)|\le\|f\|_X\int_0^1\frac{1}{|x-y|^{1/2}}\,dy\end{align*}
は直ちに得られますし,$\int_0^1\frac{1}{|x-y|^{1/2}}\,dy$は厳密に計算できますから,この積分が作用素ノルム$\|T\|$になっていそうですね.
解答例
(1)の解答
任意に$a\in[0,1]$をとる.$\phi:\R\to\overline{\R}$を
\begin{align*}\phi(y)=\begin{cases}\frac{1}{|a-y|^{1/2}},&0\le y\le1,\\0,&\text{other}\end{cases}\end{align*}
で定める($\overline{\R}$は拡大実数).任意の$h\in\R\setminus\{0\}$に対して,
\begin{align*}|Tf(a+h)-Tf(a)|&=\abs{\int_{[0,1]}\frac{f(y)}{|a+h-y|^{1/2}}-\frac{f(y)}{|a-y|^{1/2}}\,dy}
\\&\le\|f\|_X\int_{[0,1]}|\phi(y-h)-\phi(y)|\,dy\end{align*}
である.ここで,
\begin{align*}\int_{[0,1]}\phi(y)\,dy&\le\int_{[0,a]}\frac{1}{|a-y|^{1/2}}\,dy+\int_{[a,1]}\frac{1}{|a-y|^{1/2}}\,dy
\\&=\brc{2(a-y)^{1/2}}_0^a+\brc{2(y-a)^{1/2}}_a^1
\\&=2(\sqrt{a}+\sqrt{1-a})<\infty\end{align*}
だから$\phi\in L^1([0,1])$なので,$L^1$平行移動連続性より
\begin{align*}\lim_{h\to0}\int_{[0,1]}|\phi(y-h)-\phi(y)|\,dy=0\end{align*}
が成り立つ.よって,$\lim\limits_{h\to0}|Tf(a+h)-Tf(a)|=0$が成り立つから$Tf$は$a$で連続である.$a\in[0,1]$は任意だから$Tf$は$[0,1]$上連続である.
(2)の解答
任意の$f\in X$に対して,
\begin{align*}\|Tf\|_X\le\|f\|_X\esssup_{x\in[0,1]}\int_0^1\frac{1}{|x-y|^{1/2}}\,dy\end{align*}
が成り立ち,(1)の$\phi$の積分と同様に
\begin{align*}\int_{[0,1]}\frac{1}{|x-y|^{1/2}}\,dy&=2(\sqrt{x}+\sqrt{1-x})=2(\sin{\theta}+\cos{\theta})
\\&=2\sqrt{2}\sin{\bra{\theta+\frac{\pi}{4}}}\le2\sqrt{2}\end{align*}
である.ただし,$x=\sin^2{\theta}$($0\le\theta\le\frac{\pi}{2}$)とおいた.$\theta=\frac{\pi}{4}$で最後の不等号で等号が成立するから,
\begin{align*}\|Tf\|_X\le\|f\|_X\esssup_{x\in[0,1]}\int_{[0,1]}\frac{1}{|x-y|^{1/2}}\,dy=2\sqrt{2}\|f\|_X\end{align*}
が成り立ち,$\|T\|\le2\sqrt{2}$が従う.
一方,$f(x)\equiv1$とすると,
\begin{align*}\|Tf\|_X=\esssup_{x\in[0,1]}\int_{[0,1]}\frac{1}{|x-y|^{1/2}}\,dy=2\sqrt{2}=2\sqrt{2}\|f\|_X\end{align*}
となるので,$\|T\|\ge2\sqrt{2}$が従う.よって,$\|T\|=2\sqrt{2}$を得る.
(3)の解答
$\|Tf\|_X=\|T\|\|f\|_X$を満たす定数関数でない$f\in X$が存在すると仮定する.
もし$|f|$が定数関数でなければ,ある測度正の可測集合$A\subset[0,1]$が存在して,$x\in A$なら$|f(x)|<\|f\|_X$が成り立ち,任意の$x\in[0,1]$に対して
\begin{align*}&\abs{\int_{[0,1]}\frac{f(y)}{|x-y|^{1/2}}\,dy}
\\&\le\int_{A}\frac{|f(y)|}{|x-y|^{1/2}}\,dy+\int_{[0,1]\setminus A}\frac{|f(y)|}{|x-y|^{1/2}}\,dy
\\&<\int_{A}\frac{\|f\|_X}{|x-y|^{1/2}}\,dy+\int_{[0,1]\setminus A}\frac{|f(y)|}{|x-y|^{1/2}}\,dy
\\&\le\int_{[0,1]}\frac{\|f\|_X}{|x-y|^{1/2}}\,dy\end{align*}
となるから$\|Tf\|_X<\|T\|\|f\|_X$であり,これは矛盾である.よって,ある定数$k>0$と測度正の可測集合$B\subset[0,1]$が存在して
\begin{align*}f(x)=\begin{cases}k,&x\in B,\\-k,&x\notin B\end{cases}\end{align*}
となるが,任意の$x\in[0,1]$に対して
\begin{align*}&\abs{\int_{[0,1]}\frac{f(y)}{|x-y|^{1/2}}\,dy}
\\&=\abs{\int_{B}\frac{k}{|x-y|^{1/2}}\,dy+\int_{[0,1]\setminus B}\frac{-k}{|x-y|^{1/2}}\,dy}
\\&<\int_{B}\frac{k}{|x-y|^{1/2}}\,dy+\int_{[0,1]\setminus B}\frac{k}{|x-y|^{1/2}}\,dy
\\&=\int_{[0,1]}\frac{k}{|x-y|^{1/2}}\,dy\end{align*}
となるから$\|Tf\|_X<\|T\|\|f\|_X$であり,これは矛盾である.以上より,$\|Tf\|_X=\|T\|\|f\|_X$を満たす$f\in X$は定数関数である.
第10問(測度論)
$(\Omega,\mathcal{F},\mu)$を測度空間で$\mu(\Omega)=1$を満たすとする.$\Omega$上の$\mu$-可積分である実数値関数からなるバナッハ空間を$L^1(\Omega)$で表す.次の問に答えよ.
- 任意の正の定数$a$と$f\in L^1(\Omega)$に対して\begin{align*}\mu(|f|\ge a)\le\frac{1}{a}\int_\Omega |f(x)|\,d\mu(x)\end{align*}となることを示せ.
- 関数列$\{f_n\}_{n\in\N}\subset L^1(\Omega)$は以下を満たすとする.
(i) $\lim\limits_{n\to\infty}\displaystyle\iint_{\Omega\times\Omega}|f_n(x)-f_n(y)|\,d\mu(x)d\mu(y)=0$,
(ii) $\sup\limits_{n\in\N}\dint_{\Omega}|f_n(x)|^2\,d\mu(x)\le1$,
(iii) $\dint_{\Omega}f_n(x)\,d\mu(x)=0$ $n=1,2,\dots$.
このとき,$\lim\limits_{n\to\infty}\dint_\Omega|f_n(x)|\,d\mu(x)=0$となることを示せ. - (2)の(i), (ii), (iii)を満たし,$\inf\limits_{n\in\N}\dint_{\Omega}|f_n(x)|^2\,d\mu(x)>0$となるような測度空間$(\Omega,\mathcal{F},\mu)$と関数列$\{f_n\}_{n\in\N}$の例をあげよ.
(2)がメインです.(2)は条件(i)から$f_n$が定数関数に近づいていくことがみてとれ,条件(iii)からそれが0であることが分かります.
解答の方針とポイント
(1)は測度論では基本中の基本のマルコフの不等式なので瞬殺したい問題です.(2)は一様可積分性を使って欲しそうな条件が並んでいますが,実は一様可積分性を使わなくても簡単に解けます.
チェビシェフの不等式
(1)のマルコフの不等式はチェビシェフの不等式の特別な場合なので,チェビシェフの不等式を確認しておきましょう.
[チェビシェフの不等式]確率空間$(\Omega,\mathcal{F},\mu)$上の確率変数$X$を考える.任意の正値ボレル可測関数$\phi$とボレル可測集合$A$に対して,
\begin{align*}\mu(X\in A)\le\frac{E[\phi(X)]}{\inf_{x\in A}\phi(x)}\end{align*}
が成り立つ.
$X(\omega)\in A$を満たす$\omega\in\Omega$に対して,$\frac{\phi(X(\omega))}{\inf_{x\in A}\phi(x)}\ge1$が成り立つから,
\begin{align*}\mu(X\in A)&=\int_{\{X\in A\}}\,d\mu(\omega)
\le\int_{\{X\in A\}}\frac{\phi(X(\omega))}{\inf_{x\in A}\phi(x)}\,d\mu(\omega)
\\&\le\int_{\Omega}\frac{\phi(X(\omega))}{\inf_{x\in A}\phi(x)}\,d\mu(\omega)
=\frac{E[\phi(X)]}{\inf_{x\in A}\phi(x)}\end{align*}
が成り立つ.
$\phi(x)=|x|$としてできるのがマルコフの不等式ですね.
(2)の条件(i)と条件(iii)
(2)の条件(i)の
\begin{align*}\lim_{n\to\infty}\iint_{\Omega\times\Omega}|f_n(x)-f_n(y)|\,d\mu(x)d\mu(y)=0\end{align*}
より,$\Omega\times\Omega$で$|f_n(x)-f_n(y)|$がほとんど確実に0に近付くことが分かります.よって,$\Omega$上で$f_n$はほとんど確実に定数関数$C$に近付くということになりますね.
さらに条件(iii)より$f_n$の$\Omega$上の平均は0なので$C=0$となりそうです.
そこで,条件(i)の$\Omega\times\Omega$上の積分についてトネリの定理と三角不等式を用いると,
\begin{align*}&\iint_{\Omega\times\Omega}|f_n(x)-f_n(y)|\,d\mu(x)d\mu(y)
\\&=\int_{\Omega}\bra{\int_{\Omega}|f_n(x)-f_n(y)|\,d\mu(y)}\,d\mu(x)
\\&\ge\int_{\Omega}\abs{\int_{\Omega}(f_n(x)-f_n(y))\,d\mu(y)}\,d\mu(x)\end{align*}
となり,条件(iii)と$\mu(\Omega)=1$を併せて
\begin{align*}&\iint_{\Omega\times\Omega}|f_n(x)-f_n(y)|\,d\mu(x)d\mu(y)\ge\int_{\Omega}|f_n(x)|\,d\mu(x)\end{align*}
となります.よって,極限を取れば条件(i)と併せて$\lim\limits_{n\to\infty}\dint_{\Omega}|f_n(x)|\,d\mu(x)=0$が得られます.
この解法では条件(ii)は不要です.
解答例
(1)の解答
集合$\set{x\in\Omega}{|f(x)|\ge a}$上で$\frac{|f|}{a}\ge1$だから,
\begin{align*}\mu(|f|\ge a)&=\int_{\{|f|\ge a\}}\,d\mu(x)
\\&\le\int_{\{|f|\ge a\}}\frac{|f(x)|}{a}\,d\mu(x)
\\&\le\frac{1}{a}\int_\Omega |f(x)|\,d\mu(x)\end{align*}
が従う.
(2)の解答
もとより$0\le\int_{\Omega}|f_n(x)|\,d\mu(x)$であり,トネリの定理,三角不等式,$\mu(\Omega)=1$,条件(iii)より
\begin{align*}&\iint_{\Omega\times\Omega}|f_n(x)-f_n(y)|\,d\mu(x)d\mu(y)
\\&=\int_{\Omega}\bra{\int_{\Omega}|f_n(x)-f_n(y)|\,d\mu(y)}\,d\mu(x)
\\&\ge\int_{\Omega}\abs{\int_{\Omega}(f_n(x)-f_n(y))\,d\mu(y)}\,d\mu(x)
\\&=\int_{\Omega}|f_n(x)-0|\,d\mu(x)=\int_{\Omega}|f_n(x)|\,d\mu(x)\end{align*}
が成り立つから,条件(i)と併せて$\lim\limits_{n\to\infty}\dint_{\Omega}|f_n(x)|\,d\mu(x)=0$が従う.
(3)の解答
$(\Omega,\mathcal{F},\mu)$を$[0,1]\subset\R$上のルベーグ測度空間とし,
\begin{align*}f_n(x)=\begin{cases}n,&0\le x\le\delta,\\-n,&\delta<x\le2\delta,\\0,&2\delta<x\le1\end{cases}\end{align*}
とすると,求める例となる.ただし,$\delta=\frac{1}{2n^2}$である.実際,
\begin{align*}&\iint_{\Omega\times\Omega}|f_n(x)-f_n(y)|\,d\mu(x)d\mu(y)
\\&=\iint_{[0,\delta]\times(\delta,2\delta]\cup(\delta,2\delta]\times[0,\delta]}2n\,d\mu(x)d\mu(y)
\\&\quad+\iint_{[0,2\delta]\times(2\delta,1]\cup(2\delta,1]\times[0,2\delta]}n\,d\mu(x)d\mu(y)
\\&=2\delta^2 n+4\delta(1-2\delta) n=4\delta n-6\delta^2n
\\&=\frac{2}{n}-\frac{3}{2n^3}\xrightarrow[]{n\to\infty}0\end{align*}
だから(i)が成り立つ.また,
\begin{align*}&\sup_{n\in\N}\int_{\Omega}|f_n(x)|^2\,d\mu(x)
\\&=\sup_{n\in\N}\int_{[0,2\delta]}n^2\,d\mu(x)=\sup_{n\in\N}2n^2\delta=1\end{align*}
だから(ii)と$\inf\limits_{n\in\N}\dint_{\Omega}|f_n(x)|^2\,d\mu(x)>0$が成り立つ.さらに,
\begin{align*}\int_{\Omega}f_n(x)\,d\mu(x)
&=\int_{[0,\delta]}n\,d\mu(x)+\int_{(\delta,2\delta]}(-n)\,d\mu(x)
\\&=n\delta-n\delta=0\end{align*}
だから(iii)が成り立つ.
補足(一様可積分性)
解答例1では条件(ii)を使わずに解きましたが,出題者としては条件(ii)から得られる一様可積分性を使う想定だったように思われます.
そこで,確率変数列の一様可積分性についても解説しておきます.
確率空間$(\Omega,\mathcal{F},P)$上の実数値確率変数列$\{X_n\}_{n\in\N}$が一様可積分であるとは,
\begin{align*}\lim_{\lambda\to\infty}\sup_{n\in\N}\int_{\{|X_n|\ge\lambda\}}|X_n(\omega)|\,dP(\omega)=0\end{align*}
が成り立つことをいう.
問(1)と同様に考えれば,任意の$\lambda>0$に対して,条件(ii)より
\begin{align*}&\sup_{n\in\N}\int_{\{|f_n|\ge\lambda\}}|f_n(\omega)|\,d\mu(\omega)
\\&\le\sup_{n\in\N}\frac{1}{\lambda}\int_{\{|f_n|\ge\lambda\}}|f_n(\omega)|^2\,d\mu(\omega)
\\&\le\sup_{n\in\N}\frac{1}{\lambda}
=\frac{1}{\lambda}
\xrightarrow[]{\lambda\to\infty}0\end{align*}
が成り立ち,問題(2)の関数列$\{f_n\}$は一様可積分であることが分かります.
一様可積分性については,次の定理が重要です.
確率空間$(\Omega,\mathcal{F},P)$上の一様可積分な実数値確率変数列$\{X_n\}_{n\in\N}$と実数値確率変数列$X$を考える.このとき,次が成り立つ.
- $\{X_n\}$が$X$に概収束すれば,1次平均収束する.
- $\{X_n\}$が$X$に確率収束することと,1次平均収束することは同値である.
性質(2)は測度空間におけるルベーグの収束定理の一般化になっており,ヴィタリの収束定理といいます.
今回の問題では問(3)の例を少し工夫すれば概収束しない関数列$\{f_n\}$が作れるので,性質(2)は使えません.そのため,問(2)では$\{f_n\}$が0に確率収束することが示す方針で,1次平均収束
\begin{align*}\lim_{n\to\infty}\int_{\Omega}|f_n(x)|\,d\mu(x)=0\end{align*}
が成り立つことが証明できます.
第11問(微分方程式)
$\dint_{\R}e^{-x^2}\,dx=\sqrt{\pi}$は既知とする.次の問に答えよ.
- $\phi\in C^2(\R)$とし,$u(x,t)=\dfrac{1}{\sqrt{t}}\phi\bra{\dfrac{x}{\sqrt{t}}}$とする.$u(x,t)$が$u_t(x,t)=u_{xx}(x,t)$を$x\in\R$, $t>0$でみたすとする.このとき,$\phi$がみたす常微分方程式を求めよ.
- (1)で求めた常微分方程式を満たし,$\dint_{\R}\phi(x)\,dx=1$を満たすような$\phi$を求めよ.
- 次の初期値境界値問題を考える.
\begin{align*}\begin{cases}u_t(x,t)=u_{xx}(x,t),&t>0,x>0,\\u_x(x,t)=0,&t>0,x=0,\\u(x,0)=2e^{-x^2}\sin^2{x},&x>0.\end{cases}\end{align*}
古典解の1つを積分を用いて書け.さらにその積分を計算せよ.
(1)と(2)で得られる$\phi$からグリーン関数$G$が得られるので,$G$をもとに(3)で熱方程式の古典解を表します.
解答の方針とポイント
ガウス関数が熱方程式の典型的な解の例であること意識すると方針が立ちやすいです.
ガウス関数は熱方程式の解の典型例
定数$C>0$, $a>0$, $b\in\R$に対して,$\phi(x)=Ce^{-a(x-b)^2}$で定まる関数$\phi:\R\to\R$をガウス関数という.
線形熱方程式$u_t=u_{xx}$の解として$\frac{C}{\sqrt{t}}e^{-x^2/4t}$が挙げられることはよく知られています.
この具体形まで覚えていなくても,(1)で得られる常微分方程式$2\phi^{\prime\prime}(s)+s\phi'(s)+\phi(s)=0$の解に,ガウス関数$e^{-\alpha x^2}$があると予想すれば代入して$\alpha$を求めることができます.
さらに(1)は線形なので,定数倍しても解ですから$\int_{\R}\phi(x)\,dx=1$を満たすように定数倍すれば(2)で求める解が得られますね.
(1)の常微分方程式は2階なので,いま求めた$\phi$と線形独立な解も存在しますが,本問では全ての解を求める必要はありません.
(1)の解との合成積が求める古典解
(2)で求めた$\phi$を(1)のもとの式に代入してできる偶関数を$G(x,t)=\frac{1}{\sqrt{t}}\phi\bra{\frac{x}{\sqrt{t}}}$とし,初期条件の偶関数を$u_0(x)=2e^{-x^2}\sin^2{x}$とすると,合成積
\begin{align*}u(x,t)=(G(\cdot,t)*u_0)(x)=\int_{\R}G(x-y,t)u_0(y)\,dy\end{align*}
が求める古典解となります.形式的には
- 偏微分方程式$u_t=u_{xx}$は$G_t=G_{xx}$を満たす
- 境界条件$u_x(0,t)=0$は$G_x(\cdot,t)$が奇関数となる
- 初期条件$u(x,0)=u_0$は$\lim\limits_{t\to+0}G(x,t)=\delta_0$と($\mathcal{S}'(\R)$で)ディラックのデルタ関数に収束する
ことから分かります.これらを正当化すれば解答となります.
急減少関数の合成積も急減少関数
形式的には,偏微分方程式$u_t=u_{xx}$は
\begin{align*}u_{xx}(x,t)=(G_{xx}(\cdot,t)*u_0)(x)=(G_t(\cdot,t)*u_0)(x)=u_t(x,t)\end{align*}
として得られますが,1つ目と3つ目の等号は微分と積分の順序交換になっており正当化する必要があります.
ただ1つ目の等号$u_{xx}(\cdot,t)=G_{xx}(\cdot,t)*u_0$は次の定理から直ちに得られます.
急減少関数$f,g:\R\to\R$に対して,合成積$f*g:\R\to\R$も急減少関数で$(f*g)^{(n)}=f^{(n)}*g=f*g^{(n)}$が成り立つ.
微分と積分の順序交換
一方,3つ目の等号$G_t(\cdot,t)*u_0=u_t(x,t)$は合成積の変数に関する偏導関数ではないので,上の命題を使うことはできません.
こちらは次の微分と積分が順序交換条件を用いることで証明できます.
[微分と積分の順序交換条件]$A$を可測集合,$I$を開区間とする.$A\times I$上の可測関数$f(x,t)$は$t$について偏微分可能で,任意の$t\in I$に対して$f(\cdot,t)$は可積分であるとする.このとき,($t$によらない)ある$A$上の可測関数$g$が存在して,
- 任意の$t\in I$に対して$\abs{\frac{\partial f}{\partial t}(x,t)}\le g(x)$ a.e. $x\in A$
- $g$は$A$上可積分:$\int_{A}g(x)\,dx<\infty$
を満たすなら,任意の$t\in I$に対して
\begin{align*}\frac{d}{dt}\int_{A}f(x,t)\,dx=\int_{A}\frac{\partial f}{\partial t}(x,t)\,dx\end{align*}
が成り立つ.
この定理を使う際のポイントは
- (ほとんど至るところ)$|\frac{\partial f}{\partial t}(x,t)|\le g(x)$を満たす関数$g$をとる
- $\int_{A}g(x)\,dx<\infty$を満たす
の2つを示すことですね.定理の証明は以下の記事を参照してください.
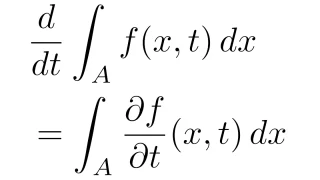
解答例
(1)の解答
$u(x,t)=\frac{1}{\sqrt{t}}\phi(\frac{x}{\sqrt{t}})$だから,
\begin{align*}u_t(x,t)&=-\frac{1}{2t\sqrt{t}}\phi\bra{\dfrac{x}{\sqrt{t}}}+\frac{1}{\sqrt{t}}\phi’\bra{\dfrac{x}{\sqrt{t}}}\bra{-\frac{x}{2t\sqrt{t}}}
\\&\quad-\frac{1}{2t\sqrt{t}}\brb{\phi\bra{\dfrac{x}{\sqrt{t}}}+\frac{x}{\sqrt{t}}\phi’\bra{\dfrac{x}{\sqrt{t}}}}
\\u_{xx}(x,t)&=\frac{1}{\sqrt{t}}\phi^{\prime\prime}\bra{\dfrac{x}{\sqrt{t}}}\bra{\frac{1}{\sqrt{t}}}^2
=\frac{1}{t\sqrt{t}}\phi^{\prime\prime}\bra{\dfrac{x}{\sqrt{t}}}\end{align*}
である.よって,$u_t(x,t)=u_{xx}(x,t)$に代入して整理すると
\begin{align*}2\phi^{\prime\prime}\bra{\dfrac{x}{\sqrt{t}}}+\phi\bra{\dfrac{x}{\sqrt{t}}}+\frac{x}{\sqrt{t}}\phi’\bra{\dfrac{x}{\sqrt{t}}}=0\end{align*}
が成り立つから,$\phi$は常微分方程式
\begin{align*}2\phi^{\prime\prime}(s)+s\phi'(s)+\phi(s)=0\quad\dots(*)\end{align*}
を満たす.
(2)の解答
常微分方程式$(*)$が$\phi(s)=Ce^{-\alpha s^2}$($\alpha>0$, $C>0$)の形の特殊解を持つと予想する.
\begin{align*}&\phi'(s)=-2C\alpha se^{-\alpha s^2},\quad
\\&\phi^{\prime\prime}(s)=-2C\alpha(1-2\alpha s^2)e^{-\alpha s^2}\end{align*}
だから,$(*)$に代入して$Ce^{-\alpha s^2}$で割って整理すると
\begin{align*}&-2\alpha(1-2\alpha s^2)+s(-2\alpha s)+1=0
\\&\iff 2\alpha(4\alpha-1)s^2+(1-4\alpha)=0\end{align*}
となるから,$\alpha=\frac{1}{4}$を得る.さらに,
\begin{align*}\int_{\R}e^{-s^2/4}\,ds=2\int_{\R}e^{-s^2}\,ds=2\sqrt{\pi}\end{align*}
だから,$\int_{\R}\phi(s)\,ds=1$を満たすには$C=\frac{1}{2\sqrt{\pi}}$とすればよく,
\begin{align*}\phi(s)=\frac{1}{2\sqrt{\pi}}e^{-s^2/4}\end{align*}
は条件を満たす$\phi$である.
(3)の解答
(2)で得た$\phi$をもとに,関数$G:[0,\infty)\times(0,\infty)\to\R$を
\begin{align*}G(x,t)=\frac{1}{\sqrt{t}}\phi\bra{\frac{x}{\sqrt{t}}}=\frac{1}{2\sqrt{\pi t}}e^{-x^2/4t}\end{align*}
と定めると,$G_t=G_{xx}$を満たす.また,関数$u_0:[0,\infty)\to\R$を
\begin{align*}u_0(x)=2e^{-x^2}\sin^2{x}\end{align*}
と定める.以下,
\begin{align*}u(x,t)=(G(\cdot,t)*u_0)(x)=\int_{\R}G(x-y,t)u_0(y)\,dy\end{align*}
で定まる関数$u:[0,\infty)\times[0,\infty)\to\R$が求める古典解であることを示す.ただし,$u(x,0)=\lim\limits_{t\to+0}u(x,t)$と定める.
[1]偏微分方程式$u_t(x,t)=u_{xx}(x,t)$を満たすことを示す.
任意の$t>0$に対して,$G(\cdot,t),u_0\in\mathcal{S}(\R)$だから,$G(\cdot,t)*u_0\in\mathcal{S}(\R)$で
\begin{align*}u_{xx}(\cdot,t)=G_{xx}(\cdot,t)*u_0=G_t(\cdot,t)*u_0\end{align*}
が成り立つから,あとは$u_t(\cdot,t)=G_t(\cdot,t)*u_0$を示せばよい.すなわち,
\begin{align*}\frac{\partial}{\partial t}(G_t(x,t)*u_0)=\frac{\partial}{\partial t}\int_{\R}G(x-y,t)u_0(y)\,dy\end{align*}
の微分と積分の順序交換が可能であることを示せばよい.
任意の$t>0$, $x\in\R$に対して,
\begin{align*}G_t(x,t)&=-\frac{1}{4t\sqrt{\pi t}}e^{-x^2/4t}+\frac{x^2}{8t^2\sqrt{\pi t}}e^{-x^2/4t}
\\&=\frac{1}{4t\sqrt{\pi t}}\bra{-1+\frac{x^2}{2t}}e^{-x^2/4t}\end{align*}
である.ここで,任意に$\delta>0$をとる.任意の$t>\delta$, $x\ge0$, $y\in\R$に対して,
\begin{align*}&|G_t(x-y,t)u_0(y)|
\\&=\abs{\frac{1}{4t\sqrt{\pi t}}\bra{-1+\frac{(x-y)^2}{2t}}e^{-(x-y)^2/4t}\cdot2e^{-y^2}\sin^2{y}}
\\&\le\frac{1}{2\delta\sqrt{\pi\delta}}\bra{1+\frac{(x-y)^2}{2\delta}}e^{-y^2}\end{align*}
が成り立つ.この最右辺は$t$によらない関数で,任意の$x\in[0,\infty)$に対して,$y$について$\R$上可積分だから,平均値の定理とルベーグの収束定理より$t>\delta$で$u_t(\cdot,t)=G_t(\cdot,t)*u_0$が成り立つ.
$\delta>0$は任意だったから,$t>0$で$u_t(\cdot,t)=G_t(\cdot,t)*u_0$が成り立つ.
[2]境界値条件$u_x(0,t)=0$を満たすことを示す.
任意の$t>0$に対して,$G(\cdot,t),u_0\in\mathcal{S}(\R)$だから,$G(\cdot,t)*u_0\in\mathcal{S}(\R)$で,任意の$t>0$に対して
\begin{align*}u_x(0,t)&=G_x(0,t)*u_0
\\&=-\int_{\R}\frac{0-y}{4t\sqrt{\pi t}}e^{-(0-y)^2/4t}\cdot2e^{-y^2}\sin^2{y}\,dy
\\&=\int_{\R}\frac{y}{2t\sqrt{\pi t}}\exp\bra{-\Bigl(\frac{1}{4t}+1\Bigr)y^2}\sin^2{y}\,dy\end{align*}
の被積分関数は奇関数なので,$u_x(0,t)=0$が成り立つ.
[3]初期条件$u(x,0)=u_0(x)$を満たすことを示す.とくに$\|\cdot\|$を$[0,\infty)$上の一様ノルムとして,$\lim\limits_{t\to+0}\|u(\cdot,t)-u_0\|=0$が成り立つことを示す.
任意に$\epsilon>0$をとる.$u_0$は一様連続なので,ある$\delta>0$が存在して,
\begin{align*}|x-y|<\delta\Ra|u_0(x)-u_0(y)|<\epsilon\end{align*}
が成り立つ.ここで,任意の$x\ge0$に対して,$\int_{\R}G(x-y,t)\,dy=1$であることより
\begin{align*}&|u(x,t)-u_0(x)|
\\&=\abs{\int_{\R}G(x-y,t)u_0(y)\,dy-\int_{\R}G(x-y,t)u_0(x)\,dy}
\\&\le\int_{\{|x-y|\ge\delta\}}G(x-y,t)|u_0(y)-u_0(x)|\,dy
\\&\quad+\int_{\{|x-y|\le\delta\}}G(x-y,t)|u_0(y)-u_0(x)|\,dy\end{align*}
となり,第1項目について
\begin{align*}&\int_{\{|x-y|\ge\delta\}}G(x-y,t)|u_0(y)-u_0(x)|\,dy
\\&\le\int_{\{|x-y|\ge\delta\}}\frac{1}{2\sqrt{\pi t}}e^{-(x-y)^2/4t}\cdot2\|u_0\|\,dy
\\&=\frac{2\|u_0\|}{\sqrt{\pi t}}\int_{\delta}^{\infty}e^{-s^2/4t}\,ds
\le\frac{2\|u_0\|}{\sqrt{\pi t}}\int_{\delta}^{\infty}e^{-\delta s/4t}\,ds
\\&=\frac{2\|u_0\|}{\sqrt{\pi t}}\brc{-\frac{4t}{\delta}e^{-\delta s/4t}}_{\delta}^{\infty}
\\&=\frac{8\|u_0\|\sqrt{t}}{\delta\sqrt{\pi}}e^{-\delta^2/4t}
\xrightarrow[]{t\to+0}0\end{align*}
が成り立ち,第2項目について
\begin{align*}&\int_{\{|x-y|\le\delta\}}G(x-y,t)|u_0(y)-u_0(x)|\,dy
\\&\le\int_{\{|x-y|\le\delta\}}G(x-y,t)\epsilon\,dy
\\&\le\epsilon\int_{\R}G(x-y,t)\,dy=\epsilon\end{align*}
が成り立つ.よって,$\lim\limits_{t\to+0}\|u(\cdot,t)-u_0\|\le\epsilon$が成り立つから,$\epsilon>0$の任意性より$\lim\limits_{t\to+0}\|u(\cdot,t)-u_0\|=0$を得る.
第12問(複素解析)
$D$を原点$z=0$を含む複素平面$\C$内の領域,$f$を$D$上の正則関数とする.$f$の零点の位数は全て1であるとし,$f(0)\neq0$とする.各$r>0$に対し$B_r=\{z\in\C;|z|<r\}$, $\overline{B}_r=\{z\in\C;|z|\le r\}$とおく.また
\begin{align*}S=\{r\in\R;r>0,\overline{B}_r\subset D,\text{$f$は$\{z\in\C;|z|=r\}$上に零点を持たない}\}\end{align*}
とおく.
- $r\in S$とする.$f$は$B_r$内に零点を持つとし,$B_r$に含まれる$f$の零点全体を$a_1,\dots,a_n$とする.このとき,
\begin{align*}\frac{1}{2\pi}\int_{0}^{2\pi}\log{|f(re^{i\theta})|}\,d\theta\end{align*}
の値を$f(0),r,a_1,\dots,a_n$で表せ. - 各$r>0$に対し
\begin{align*}L(r)=\frac{1}{2\pi}\int_{0}^{2\pi}\max\{\log{|f(re^{i\theta})|},0\}\,d\theta,\quad
M(r)=\max\{|f(z)|;z\in\overline{B}_r\}\end{align*}
とおく.$1\in S$とする.このとき,$0<r<1$なる任意の$r\in S$に対して
\begin{align*}L(r)\le\max\{\log{M(r)},0\}\le\frac{1+r}{1-r}L(1)\end{align*}
が成り立つことを示せ.
(1)はイェンセンの公式を導く問題で,(2)はほとんどハルナックの不等式を示す問題です.
解答の方針とポイント
(1)の積分の形から平均値の性質を使う方針が見えます.(2)は右の不等式の$\log{M(r)}$の評価が最も難しく,ここで(1)を使います.
平均値の性質
領域$D$上の正則関数$\phi:D\to\C$に対して,$\alpha$中心,半径$r$の閉円板が$D$に含まれるときコーシーの積分公式
\begin{align*}\phi(\alpha)=\frac{1}{2\pi i}\int_{|z-\alpha|=r}\frac{\phi(z)}{z-\alpha}\,dz\end{align*}
が成り立ちます.$z=\alpha+re^{i\theta}$と置き換えると,右辺は「$\alpha$中心の円周上の値の平均」となり,この正則関数の性質を(正則関数の)平均値の性質といいます.
[平均値の性質]領域$D$と正則関数$\phi:D\to\C$を考える.$\set{z\in\C}{|z-a|\le r}\subset D$なる$a\in D$, $r>0$に対して,
\begin{align*}\phi(a)=\frac{1}{2\pi}\int_{0}^{2\pi}\phi(a+re^{i\theta})\,d\theta\end{align*}
が成り立つ.
両辺で実部と虚部をそれぞれ考えると,正則関数の実部と虚部についても同様に平均値の性質が成り立つことが分かります.
一般に$\log{z}=\log{|z|}+i\arg{z}$ですから,もし$\log{f}$が$B_r$全体で定義されていれば(すなわち$f$が$B_r$に零点をもたなければ),0中心で$\log{f}$について平均値の性質を用いて実部をとれば,本問(1)で考える$\log{|f(re^{i\theta})|}$の積分が得られます.
しかし,本問(1)では$f$が一位の零点$a_1,a_2,\dots,a_n$をもつので,
\begin{align*}g(z)=\frac{f(z)}{(z-a_1)(z-a_2)\dots(z-a_n)}\end{align*}
で零点を消した正則関数$g$を定めれば,$\log{g}$について平均値の性質を適用することができ,対数の性質と併せて目的の$\log{|f(re^{i\theta})|}$の積分が得られます.
$\tilde{g}(z)=f(f)\prod\limits_{k=1}^{n}\frac{r^2-\bar{a}_kz}{r(z-a_k)}$とおいて,$|z|=r$上で$|f(z)|=|\tilde{g}(z)|$であることを利用すれば,もっと簡単な計算で解けますが,この$\tilde{g}$に気付くのは難しいので,解答では上の$g$を用いて解いています.
単位円板上の正則自己同型
(2)で示す不等式について,左の不等式の証明は簡単で,右の不等式も$0\le\frac{1+r}{1-r}L(1)$の証明は簡単なので,$\log{M(r)}\le\frac{1+r}{1-r}L(1)$の証明が本質的な問題です.最大絶対値の原理より
\begin{align*}M(r)=\max_{|z|\le r}|f(z)|=\max_{|z|=r}|f(z)|\end{align*}
ですから,$M(r)=|f(\alpha)|$かつ$|\alpha|=r$となる$\alpha\in\C$が存在するので,$L(1)$も定義から書き直して
\begin{align*}\log{|f(\alpha)|}\le\frac{1+r}{1-r}\cdot\frac{1}{2\pi}\int_{0}^{2\pi}\max\{\log{|f(e^{i\theta})|},0\}\,d\theta\end{align*}
を示すことになります.
いかにも(1)を使いそうですが,左辺は$\log{|f(\alpha)|}$なので,このままでは(1)を適用できません.そこで,$\phi_\alpha(\alpha)=0$となる全単射な正則関数$\phi_\alpha:B_1\to B_1$で$\alpha$と原点を対応させましょう.
単位開円板$B_1$と$\alpha\in B_1$に対して,$\phi_\alpha(\alpha)=0$を満たす全単射な正則関数$\phi_\alpha:B_1\to B_1$は
\begin{align*}\phi_\alpha(z)=\frac{z-\alpha}{1-\bar{\alpha}z}e^{i\theta}\end{align*}
と表せる($\theta\in\R$).
この定理はシュワルツの補題の系として証明されますね.
そこで$F=f\circ\phi_\alpha^{-1}$とおけば,(1)と併せて
\begin{align*}\log{|f(\alpha)|}&=\log{|F\circ\phi_\alpha(\alpha)|}=\log{|F(0)|}
\\&\le\frac{1}{2\pi}\int_{0}^{2\pi}\log{|F(e^{i\theta})|}\,d\theta\end{align*}
と評価できます.あとは右辺の積分で$\phi_\alpha^{-1}(e^{i\theta})=e^{i\varphi}$と置換すれば$f(e^{i\varphi})$の積分となり,$\frac{d\theta}{d\varphi}$の部分が$\frac{1+r}{1-r}$で評価できるので,$\log{M(r)}\le\frac{1+r}{1-r}L(1)$が得られます.
解答例
$r\in S$のとき,$f$は$|z|=r$上に零点をもたず$f$の零点は離散なので,ある$r<s$を満たす$s\in S$が存在し,$B_r$に含まれる$f$の零点全体と$B_s$に含まれる$f$の零点全体は一致する.
また,一般に領域上で恒等的に0でない関数の零点全部の集合は領域上に集積点を持たないことと併せると,$r\in S$のとき$B_r$に含まれる$f$の零点は有限個であることも分かる.
(1)の解答
$r<s$かつ$B_s$に含まれる$f$の零点全体が$a_1,\dots,a_n$となる$s\in S$をとる.正則関数$g:B_s\to\mathbb{C}$を
\begin{align*}g(z)=f(z)\prod_{k=1}^{n}(z-a_k)^{-1}\end{align*}
で定める.ただし,各$a_k$は$g$の除去可能な特異点なので,$g$が正則となるように定める.
$f$の全ての零点が一位であることから$g$は単連結領域$B_s$上で零点をもたないので$\log{g(z)}$は$B_s$上正則となる.よって,$\log{g(z)}$に平均値の性質が適用できて,$\log{|g(z)|}=\operatorname{Re}\log{g(z)}$だから実部をとれば
\begin{align*}\log{|g(0)|}=\frac{1}{2\pi}\int_{0}^{2\pi}\log{|g(re^{i\theta})|}\,d\theta\end{align*}
が成り立つ.左辺は
\begin{align*}&\log{|g(0)|}=\log{|f(0)|}-\sum_{k=1}^{n}\log{|a_k|}\end{align*}
であり,右辺は
\begin{align*}&\int_{0}^{2\pi}\log{|g(re^{i\theta})|}\,d\theta
\\&=\int_{0}^{2\pi}\log{|f(re^{i\theta})|}\,d\theta-\sum_{k=1}^{n}\int_{0}^{2\pi}\log{|re^{i\theta}-a_k|}\,d\theta
\\&=\int_{0}^{2\pi}\log{|f(re^{i\theta})|}\,d\theta-2n\pi\log{r}-\sum_{k=1}^{n}\int_{0}^{2\pi}\log{\abs{1-\frac{a_k}{r}e^{-i\theta}}}\,d\theta\end{align*}
である.
$\log{(1-z)}$は$-\sum\limits_{m=1}^{\infty}\frac{z^m}{m}$と冪級数展開でき,この収束半径は1である.任意の$k\in\{1,2,\dots,n\}$に対して,$\abs{\frac{a_k}{r}e^{-i\theta}}<1$なので,
\begin{align*}&\int_{0}^{2\pi}\log{\abs{1-\frac{a_k}{r}e^{-i\theta}}}\,d\theta
\\&=\operatorname{Re}\int_{0}^{2\pi}\log{\bra{1-\frac{a_k}{r}e^{-i\theta}}}\,d\theta
\\&=-\operatorname{Re}\sum_{m=1}^{\infty}\frac{a_k^m}{mr^m}\int_{0}^{2\pi}e^{-im\theta}\,d\theta=0\end{align*}
が成り立つ.ただし,収束半径内($\theta$に関して一様収束)なので項別積分可能であることと,$\int_{0}^{2\pi}e^{-im\theta}\,d\theta=0$($m=1,2,\dots$)を用いた.
以上より,
\begin{align*}&\frac{1}{2\pi}\int_{0}^{2\pi}\log{|f(re^{i\theta})|}\,d\theta
\\&=\log{|f(0)|}-\sum_{k=1}^{n}\log{|a_k|}+\sum_{k=1}^{n}\log{r}
\\&=\log{|f(0)|}+\sum_{k=1}^{n}\log{\frac{r}{|a_k|}}\end{align*}
を得る.
(2)の解答
[左側の不等式の証明]$M(r)\le1$なら,$\max\{\log{|f(re^{i\theta})|},0\}=0$なので
\begin{align*}L(r)=0=\max\{\log{M(r)},0\}\end{align*}
が成り立つ.一方,$M(r)>1$なら,$\max\{\log{|f(re^{i\theta})|},0\}\le \log{M(r)}$なので
\begin{align*}L(r)\le\log{M(r)}\le\max\{\log{M(r)},0\}\end{align*}
が成り立つ.
[右側の不等式の証明]$0\le\max\{\log{|f(e^{i\theta})|},0\}$かつ$0<r<1$なので,$0\le\frac{1+r}{1-r}L(1)$が成り立つ.よって,あとは$\log{M(r)}\le\frac{1+r}{1-r}L(1)$が成り立つことを示せばよい.
最大絶対値の原理より,$|\alpha|=r$を満たすある$\alpha\in\C$が存在し,$M(r)=|f(\alpha)|$が成り立つ.連続関数$\phi_\alpha:\overline{B}_1\to\overline{B}_1$, $F:\overline{B}_1\to\mathbb{C}$を
\begin{align*}\phi_\alpha(z)=\frac{z-\alpha}{1-\bar{\alpha}z},\quad
F=f\circ\phi_\alpha^{-1}\end{align*}
で定める.このとき,$\phi_\alpha$, $F$はともに$B_1$上正則で,さらに$\phi_\alpha$は全単射かつ
\begin{align*}\phi’_\alpha(z)=\frac{(1-\bar{\alpha}z)-(z-\alpha)(-\bar{\alpha})}{(1-\bar{\alpha}z)^2}=\frac{1-r^2}{(1-\bar{\alpha}z)^2}\end{align*}
である.
(1)の解答の前に述べたことから$f$は$B_1$上に零点を無限個もたないので,$F=f\circ\phi_\alpha^{-1}$も$B_1$上に零点を無限個もたない.$F$が零点をもつなら,零点全体を$b_1,\dots,b_m$とすると,$|F(0)|=|f(\alpha)|=M(r)\neq0$だから,(1)が適用できて
\begin{align*}\log{M(r)}&=\log{|f(\alpha)|}=\log{|F\circ\phi_\alpha(\alpha)|}=\log{|F(0)|}
\\&=\frac{1}{2\pi}\int_{0}^{2\pi}\log{|F(e^{i\theta})|}\,d\theta-\sum_{k=1}^{m}\log{\frac{1}{|b_k|}}
\\&\le\frac{1}{2\pi}\int_{0}^{2\pi}\log{|F(e^{i\theta})|}\,d\theta\end{align*}
が成り立つ.$F$が零点をもたなければ,$\log{F}$に平均値の性質を適用して実部をとれば
\begin{align*}\log{M(r)}=\log{|F(0)|}=\frac{1}{2\pi}\int_{0}^{2\pi}\log{|F(e^{i\theta})|}\,d\theta\end{align*}
が成り立つ.
ここで,$\phi_\alpha(e^{i\varphi})=e^{i\theta}$とおくと$\phi’_\alpha(e^{i\varphi})ie^{i\varphi}=ie^{i\theta}\frac{d\theta}{d\varphi}$なので,
\begin{align*}\frac{d\theta}{d\varphi}&=\frac{\phi’_\alpha(e^{i\varphi})}{\phi_\alpha(e^{i\varphi})}e^{i\varphi}
=\frac{1-r^2}{(1-\bar{\alpha}e^{i\varphi})^2}\cdot\frac{1-\bar{\alpha}e^{i\varphi}}{e^{i\varphi}-\alpha}e^{i\varphi}
\\&=\frac{1-r^2}{(1-\bar{\alpha}e^{i\varphi})\overline{(1-\bar{\alpha}e^{i\varphi})}}
=\frac{1-r^2}{|1-\bar{\alpha}e^{i\varphi}|^2}
\\&\le\frac{1-r^2}{(1-r)^2}=\frac{1+r}{1-r}\end{align*}
である.以上を併せて
\begin{align*}\log{M(r)}&\le\frac{1}{2\pi}\int_{0}^{2\pi}\log{|F(e^{i\theta})|}\,d\theta
\\&\le\frac{1}{2\pi}\int_{0}^{2\pi}\max\{\log{|F(e^{i\theta})|},0\}\,d\theta
\\&=\frac{1}{2\pi}\int_{0}^{2\pi}\max\{\log{|f(e^{i\varphi})|},0\}\frac{d\theta}{d\varphi}\,d\varphi
\\&\le\frac{1+r}{1-r}\cdot\frac{1}{2\pi}\int_{0}^{2\pi}\max\{\log{|f(e^{i\varphi})|},0\}\,d\varphi
\\&=\frac{1+r}{1-r}L(1)\end{align*}
を得る.
補足(イェンセンの公式とポアソンの公式)
(1)で正則関数の平均値の性質と零点の処理で示した等式
\begin{align*}\frac{1}{2\pi}\int_{0}^{2\pi}\log{|f(re^{i\theta})|}\,d\theta=\log{|f(0)|}+\sum_{k=1}^{n}\log{\frac{r}{|a_k|}}\end{align*}
はイェンセンの公式と呼ばれており,円周上での値(の絶対値)と零点(の絶対値)の関係を述べる等式です.また,(2)の解答例ではイェンセンの公式と単位円板の正則自己同型を用いて解きました.
つまり,本問の(2)を解くためのポイントは
- 正則関数の平均値の性質
- 零点の処理
- 単位円板の正則自己同型
の3つだったということになります.これらのうち,(i)と(iii)を用いて示される定理が次のポアソンの公式です.
[ポアソンの公式]複素関数$u$は$\overline{B}_R$で連続,$B_R$で調和であるとする.このとき,任意の$|\alpha|<R$に対して,
\begin{align*}u(\alpha)=\frac{1}{2\pi}\int_{|z|=R}\frac{R^2-|\alpha|^2}{|z-\alpha|^2}u(z)\,dz\end{align*}
が成り立つ.
そのため,上の(2)の解答例では本質的にはイェンセンの公式とポアソンの公式を併せて解いたと捉えることができます.
実際,(i), (ii), (iii)を全て用いて示されるイェンセン-ポアソンの公式と呼ばれる定理があり,イェンセン-ポアソンの公式を使えば(2)は簡単に解くことができます.
参考文献
基礎を固めるために私が実際に使ったオススメの入試問題集を挙げておきます.
詳解と演習大学院入試問題〈数学〉
[海老原円,太田雅人 共著/数理工学社]
理工系の修士課程への大学院入試問題集ですが,基礎〜標準的な問題が広く大学での数学の基礎が復習できる総合問題集として利用することができます.
実際,まえがきにも「単なる入試問題の解説にとどまらず,それを通じて,数学に関する読者の素養の質を高めることにある」と書かれているように,必ずしも大学院入試を受験しない一般の学習者にとっても学びやすい問題集です.また,構成が読みやすいのも個人的には嬉しいポイントです.
第1章 数え上げと整数
第2章 線形代数
第3章 微積分
第4章 微分方程式
第5章 複素解析
第6章 ベクトル解析
第7章 ラプラス変換
第8章 フーリエ変換
第9章 確率
一方で,問題数はそれほど多くないので,多くの問題を解きたい方には次の問題集もオススメです.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの問題集|詳解と演習 大学院入試問題(数理工学社)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.
演習 大学院入試問題
[姫野俊一,陳啓浩 共著/サイエンス社]
上記の問題集とは対称的に問題数が多く,まえがきに「修士の基礎数学の問題の範囲は,ほぼ本書中に網羅されている」と書かれているように,広い分野から問題が豊富に掲載されています.
全2巻で,
1巻第1編 線形代数
1巻第2編 微分・積分学
1巻第3編 微分方程式
2巻第4編 ラプラス変換,フーリエ変換,特殊関数,変分法
2巻第5編 複素関数論
2巻第6編 確率・統計
が扱われています.
地道にきちんと地に足つけた考え方で解ける問題が多く,確かな「腕力」がつくテキストです.入試では基本問題は確実に解けることが大切なので,その意味で試験への対応力が養われると思います.
なお,私自身は受験生時代に計算力があまり高くなかったので,この本の問題で訓練したのを覚えています.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの問題集|演習 大学院入試問題[数学](サイエンス社)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.




コメント