ペロン-フロベニウスの定理とは,全ての成分が正の正方行列または全ての成分が非負の正方行列の最大固有値に関する定理です.
歴史的には
- 成分が正の正方行列に対する場合(Oskar Perron)
- 成分が非負の正方行列に対する場合(Ferdinand Georg Frobenius)
の順に示されました.
この記事では
- 2種類のペロン・フロベニウスの定理
- 正行列のペロン・フロベニウスの定理の具体例
- 正行列のペロン・フロベニウスの定理の証明
を順に解説します.
多項式$f(x)$に正方行列$A$を代入してできる正方行列$f(A)$の固有値に関するフロベニウスの定理とは別の定理です.
2種類のペロン・フロベニウスの定理
冒頭でも触れたように,ペロン-フロベニウスの定理は成分が正の場合・非負(0以上)の場合の2通りあります.
正行列・非負行列は正方行列の定値性(正定値・不定値)とは別物です.
正行列に対するペロン-フロベニウスの定理
別の書き方をすると「$A$の全ての固有値の絶対値の大小を比較したとき,絶対値が最大の固有値$\alpha$はもともと正の数であって,(2), (3)が成り立つ」という定理ですね.
非負行列に対するペロン-フロベニウスの定理
成分が非負の正方行列の場合には,結論が少し弱くなりますが次が成り立ちます.
[非負行列のペロン-フロベニウスの定理]非負の正方行列$A$は次を満たす非負の固有値$\alpha$をもつ.
- $A$の任意の固有値$\beta$に対して,$|\beta|\le\alpha$が成り立つ.
- 固有値$\alpha$に属する非負の固有ベクトルが存在する.
非負の場合は最大固有値$\alpha$の(代数的)重複度は1とは限らなくなり,(代数的)重複度が1でない場合は非負でない固有ベクトルをもつこともあります.
正行列に対するペロン・フロベニウスの定理の具体例
$A$の固有多項式は
\begin{align*}|xI-A|&=\vmat{x-1&-2&-2\\-3&x-1&-1\\-2&-1&x-2}
=\vmat{x-5&-2&-2\\x-5&x-1&-1\\x-5&-1&x-2}
\\&=(x-5)\vmat{1&-2&-2\\1&x-1&-1\\1&-1&x-2}
=(x-5)\vmat{1&-2&-2\\0&x+1&1\\0&1&x}
\\&=(x-5)\vmat{x+1&1\\1&x}
=(x-5)(x^2+x-1)\end{align*}
なので,$A$の固有値は$5,\dfrac{-1\pm\sqrt{5}}{2}$である.
よって,$A$の固有値のうち最大のものは5で,これは確かに正で(代数的)重複度は1となっている.
最大固有値に属する固有ベクトル
行基本変形により
\begin{align*}A-5I&=\bmat{-4&2&2\\3&-4&1\\2&1&-3}\to\bmat{0&4&-4\\1&-5&4\\2&1&-3}
\\&\to\bmat{0&4&-4\\1&-5&4\\0&11&-11}\to\bmat{0&1&-1\\1&0&-1\\0&0&0}\end{align*}
となるので,掃き出し法により$A$の固有値5に属する固有ベクトルとして$\bmat{1\\1\\1}$を得る.
この固有ベクトルは確かに正ベクトルである.
最大固有値以外の固有値に属する固有ベクトル
$\alpha:=\dfrac{-1\pm\sqrt{5}}{2}$とおくと,行基本変形により
\begin{align*}A-\alpha I&=\bmat{1-\alpha&2&2\\3&1-\alpha&1\\2&1&2-\alpha}=\bmat{1-\alpha&2&2\\1&-\alpha&\alpha-1\\2&1&2-\alpha}
\\&\to\bmat{0&2-\alpha(\alpha-1)&2+(\alpha-1)^2\\1&-\alpha&\alpha-1\\ 0&1+2\alpha&4-3\alpha}
\\&=\bmat{0&-\alpha^2+\alpha+2&\alpha^2-2\alpha+3\\1&-\alpha&\alpha-1\\ 0&1+2\alpha&4-3\alpha}\end{align*}
となる.$\alpha$は方程式$x^2+x-1=0$の解として得られていたから$\alpha^2+\alpha-1=0$が成り立つことに注意すると,さらに
\begin{align*}A-\alpha I&\to\bmat{0&1+2\alpha&4-3\alpha\\1&-\alpha&\alpha-1\\ 0&1+2\alpha&4-3\alpha}
\to\bmat{0&1+2\alpha&4-3\alpha\\1&-\alpha&\alpha-1\\ 0&0&0}\end{align*}
となる.よって,掃き出し法により$A$の固有値$\dfrac{-1-\sqrt{5}}{2}$に属する固有ベクトルは$k\bmat{-4\alpha+2\\3\alpha-4\\2\alpha+1}$となる($k\in\R\setminus\{0\}$).
$\alpha=\dfrac{-1\pm\sqrt{5}}{2}$のどちらでも固有値$\alpha$の固有ベクトルが正ベクトルになることはないことが確認でき,確かに最大固有値以外は正ベクトルを持たない.
ペロン-フロベニウスの定理を使えば,以上の計算を全くする必要なく(1)〜(3)の条件を満たす正の固有値が存在していることが分かるわけですね.
正行列のペロン・フロベニウスの定理の証明
この記事では,正の正方行列に対するペロン-フロベニウスの定理を証明します.
非負の正方行列に対するペロン-フロベニウスの定理の証明については,この記事の最後で紹介している参考文献を参照してください.
[正行列のペロン-フロベニウスの定理(再掲)]正の正方行列$A$は次を満たす正の固有値$\alpha$をもつ.
以下では
- $A=(a_{ij})$は$N$次正方行列
- $\m{x}\in\R^N$の第$i$成分を$[\m{x}]_i$
- $\|\cdot\|$を成分の最大値ノルム:$\|\m{x}\|:=\max\limits_{i\in\{1,\dots,N\}}|[\m{x}]_i|$
- $I$を$N$次単位行列
とし,6ステップに分けて証明します.
ステップ1(漸化式を満たす正ベクトルの列)
正ベクトルの点列$\{\m{u}_n\}_{n=0}^{\infty}$で,任意の$n\in\{0,1,2,\dots\}$に対し
\begin{align*}\m{u}_{n+1}=\frac{A\m{u}_n}{\|A\m{u}_n\|},\quad
\|\m{u}_{n}\|=1\quad\dots(\star)\end{align*}
を満たすものが存在する.
具体的に構成する.$\m{u}_0:=\sbmat{1\\\vdots\\1}\in\R^N$とおき,$\m{u}_1,\m{u}_2,\dots$を
\begin{align*}\m{u}_{n+1}:=\frac{A\m{u}_n}{\|A\m{u}_n\|}\end{align*}
で帰納的に定義する.このときの点列$\{\m{u}_n\}$が条件を満たすことを,数学的帰納法により示す.
[1]$\m{u}_0$は全ての成分が1なので正ベクトルであり,$\|\cdot\|$は最大値ノルムとしているから$\|\m{u}_0\|=1$を満たす.
[2]$\m{u}_k$は正ベクトルであり,$n=k$で条件$(\star)$を満たすとする($k=1,2,\dots$).
このとき,$\m{u}_k$は正ベクトルなので,$A$が正行列であることと併せて$A\m{u}_k$は正行列である.よって,
\begin{align*}\m{u}_{k+1}=\frac{A\m{u}_k}{\|A\m{u}_k\|}\end{align*}
も正ベクトルである.また,ノルムの斉次性より
\begin{align*}\|\m{u}_{k+1}\|=\nor{\frac{A\m{u}_k}{\|A\m{u}_k\|}}=\frac{1}{\|A\m{u}_k\|}\|A\m{u}_k\|=1\end{align*}
をみたす.
[1]と[2]より,正ベクトルの点列$\{\m{u}_n\}_{n=0}^{\infty}$で,任意の$n\in\{0,1,2,\dots\}$に対し$(\star)$を満たすものが存在する.
のちのステップ3で,この点列$\{\m{u}_n\}$の部分列が収束して,このときの極限$\m{u}$が$A$の固有ベクトルとなることを示します.
ステップ2(最大固有値となる$\alpha$の導入)
関数$f:(\R_{>0})^N\to\R$を
\begin{align*}f(\m{x}):=\min_{i=1,\dots,N}\frac{[A\m{x}]_i}{[\m{x}]_i}\end{align*}
で定める.このとき,ステップ1の$\{\m{u}_n\}$に対して,$\alpha:=\lim\limits_{n\to\infty}f(\m{u}_n)$が存在し,$\alpha>0$が成り立つ.
$(\R_{>0})^N$は正ベクトル全部の集合(正の実数全部の集合$\R_{>0}$の$N$個の直積)です.
数列$\{f(\m{u}_n)\}$で単調有界実数列の収束定理を用いるために,数列$\{f(\m{u}_n)\}$が単調増加し,上に有界であることを示す.
$(A-f(\m{u}_n)I)\m{u}_{n+1}$が非負ベクトルであることの証明
任意の$n\in\{0,1,2,\dots\}$に対して,
ベクトル$(A-f(\m{u}_n)I)\m{u}_n$の第$i$成分($i=1,\dots,N$)は
\begin{align*}[(A-f(\m{u}_n)I)\m{u}_n]_i
&=[A\m{u}_n]_i-f(\m{u}_n)[\m{u}_n]_i
\\&\ge[A\m{u}_n]_i-\frac{[A\m{u}_n]_i}{[\m{u}_n]_i}[\m{u}_n]_i
=0\end{align*}
である.よって,$(A-f(\m{u}_n)I)\m{u}_n$は非負ベクトルである.よって,これに左から成分が正の行列$\frac{A}{\|\m{u}_n\|}$をかけてできる
\begin{align*}\frac{A}{\|\m{u}_n\|}(A-f(\m{u}_n)I)\m{u}_n
&=(A-f(\m{u}_n)I)\frac{A\m{u}_n}{\|\m{u}_n\|}
\\&=(A-f(\m{u}_n)I)\m{u}_{n+1}\end{align*}
も非負ベクトルである.
数列$\{f(\m{u}_n)\}$が単調増加することの証明
任意に$n\in\{0,1,2,\dots\}$と$i=1,\dots,N$をとる.$0<[\m{u}_{n+1}]_i\le1$なので
\begin{align*}\frac{[A\m{u}_{n+1}]_i}{[\m{u}_{n+1}]_i}-f(\m{u}_n)
&=\frac{[A\m{u}_{n+1}]_i}{[\m{u}_{n+1}]_i}-\frac{f(\m{u}_n)[\m{u}_{n+1}]_i}{[\m{u}_{n+1}]_i}
\\&=\frac{[A\m{u}_{n+1}-f(\m{u}_n)\m{u}_{n+1}]_i}{[\m{u}_{n+1}]_i}
\\&\ge[A\m{u}_{n+1}-f(\m{u}_n)\m{u}_{n+1}]_i
\\&=[(A-f(\m{u}_n)I)\m{u}_{n+1}]_i\end{align*}
なので,$(A-f(\m{u}_n)I)\m{u}_{n+1}$が非負ベクトルであることと併せて
\begin{align*}&\frac{[A\m{u}_{n+1}]_i}{[\m{u}_{n+1}]_i}\ge f(\m{u}_n)\end{align*}
となるから,両辺で$\min\limits_{i\in\{1,\dots,N\}}$をとって$f(\m{u}_{n+1})\ge f(\m{u}_n)$が成り立つ.すなわち,数列$\{f(\m{u}_n)\}$は(広義)単調増加する.
数列$\{f(\m{u}_n)\}$が上に有界であることの証明
関数$F:(\R_{>0})^N\to\R$を
\begin{align*}F(\m{x}):=\max_{j=1,\dots,N}\frac{[A\m{x}]_j}{[\m{x}]_j}\end{align*}
で定める.このとき,数列$\{f(\m{u}_n)\}$が単調増加することの証明と同様に,数列$\{f(\m{u}_n)\}$は(広義)単調減少することが証明できる.
よって,$f(\m{u}_n)\le F(\m{u}_n)$に注意すれば
\begin{align*}f(\m{u}_0)\le f(\m{u}_1)\le f(\m{u}_2)\le \dots\le F(\m{u}_2)\le F(\m{u}_1)\le F(\m{u}_0)\end{align*}
が成り立つので,実数列$\{f(\m{u}_n)\}$は上に有界である($F(\m{u}_0)$が上界のひとつ).
単調有界実数列の収束定理を数列$\{f(\m{u}_n)\}$に適用
数列$\{f(\m{u}_n)\}$は単調増加し,上に有界であると分かったから,単調有界実数列の収束定理より極限
\begin{align*}\alpha:=\lim\limits_{n\to\infty}f(\m{u}_n)\end{align*}
が存在する.
また,任意の$n\in\N$に対して$0<f(\m{u}_0)\le f(\m{u}_n)$だから,$\alpha>0$である.
以降,$\alpha$はこのステップ2で定まった$\alpha$のことを指します.
ステップ3以降で,この$\alpha$が$A$の固有値であり,定理で述べた性質をもつことを示します.
ステップ3($\alpha$に属する正の固有ベクトルの存在)
任意に$n\in\N$をとる.
$\|(A-f(\m{u}_n)I)\m{u}_n\|$の評価
ステップ2で示した不等式
\begin{align*}&\frac{[A\m{u}_{n+1}]_i}{[\m{u}_{n+1}]_i}-f(\m{u}_n)\ge[(A-f(\m{u}_n)I)\m{u}_{n+1}]_i\end{align*}
と漸化式$\m{u}_{n+1}=\frac{A\m{u}_n}{\|A\m{u}_n\|}$と併せると,
\begin{align*}\frac{[A\m{u}_{n+1}]_i}{[\m{u}_{n+1}]_i}-f(\m{u}_n)
&\ge\brc{\frac{A(A-f(\m{u}_n)I)\m{u}_n}{\|A\m{u}_n\|}}_i
\\&=\frac{[A(A-f(\m{u}_n)I)\m{u}_n]_i}{\|A\m{u}_n\|}\end{align*}
を得る.この分母と分子をそれぞれ評価する.
\begin{align*}M:=\sum_{i,j=1}^{N}a_{ij},\quad
m:=\min_{i,j\in\{1,\dots,N\}}a_{ij}\end{align*}
を定めると,行列の積の定義と$A$が正行列であることより
\begin{align*}\|A\m{u}_n\|
&=\max\limits_{i\in\{1,\dots,N\}}\sum_{j=1}^{N}a_{ij}[\m{u}_n]_j
\\&\le\max\limits_{i\in\{1,\dots,N\}}\sum_{j=1}^{N}a_{ij}\cdot1
\le M\end{align*}
であり,行列の積の定義と$m$の定義より
\begin{align*}[A(A-f(\m{u}_n)I)\m{u}_n]_i
&=\sum_{j=1}^{N}a_{ij}[(A-f(\m{u}_n)I)\m{u}_n]_j
\\&\ge m\sum_{j=1}^{N}[(A-f(\m{u}_n)I)\m{u}_n]_j\end{align*}
である.よって,
\begin{align*}\frac{[A\m{u}_{n+1}]_i}{[\m{u}_{n+1}]_i}-f(\m{u}_n)
&\ge\frac{m}{M}\sum_{j=1}^{N}[(A-f(\m{u}_n)I)\m{u}_n]_j
\\&\ge\frac{m}{M}\|(A-f(\m{u}_n)I)\m{u}_n\|\end{align*}
を得る.
$(A-f(\m{u}_n)I)\m{u}_n$の極限
\begin{align*}f(\m{u}_{n+1})-f(\m{u}_n)\ge\frac{m}{M}\|(A-f(\m{u}_n)I)\m{u}_n\|\end{align*}
の左辺で極限$n\to\infty$をとると
\begin{align*}\lim_{n\to\infty}\{f(\m{u}_{n+1})-f(\m{u}_n)\}=\alpha-\alpha=0\end{align*}
なので,$\frac{m}{M}\|(A-f(\m{u}_n)I)\m{u}_n\|\ge0$と併せると,はさみうちの原理より
\begin{align*}\lim_{n\to\infty}\|(A-f(\m{u}_n)I)\m{u}_n\|=0\end{align*}
が成り立つ.よって,ノルム$\|\cdot\|$の連続性から
\begin{align*}\lim_{n\to\infty}(A-f(\m{u}_n)I)\m{u}_n=\m{0}\quad\dots(*)\end{align*}
が成り立つ.
$\alpha$が$A$の固有値で,$\alpha$に属する正の固有ベクトルが存在することの証明
点列$\{\m{u}_n\}_{n=0}^{\infty}$は有界だから,ボルツァーノ-ワイエルシュトラスの定理より収束部分列$\{\m{u}_{n(k)}\}_{k=0}^{\infty}$をもつ.この極限を$\m{u}$とする.
$\|\m{u}_{n(k)}\|=1$の両辺で極限$k\to\infty$をとると,ノルムの連続性から$\|\m{u}\|=1$となるので$\m{u}\neq\m{0}$である.
また,$\brb{(A-f(\m{u}_n)I)\m{u}_n}_{n=0}^{\infty}$の部分列$\{(A-f(\m{u}_{n(k)})I)\m{u}_{n(k)}\}_{k=0}^{\infty}$の極限は
\begin{align*}\lim_{k\to\infty}(A-f(\m{u}_{n(k)})I)\m{u}_{n(k)}=(A-\alpha I)\m{u}\quad\dots(**)\end{align*}
となる.一般にもとの点列の極限が存在すれば任意の部分列の極限と一致するから,$(*)$と$(**)$より
\begin{align*}(A-\alpha I)\m{u}=\m{0}
\iff A\m{u}=\alpha\m{u}\end{align*}
となる.よって,$\alpha$は$A$の固有値であり,$\m{u}$は$A$の固有値$\alpha$の固有ベクトルであることが示された.
$\{\m{u}_n\}$は正ベクトルの列だから$\m{u}$は非負ベクトルである.また,$\m{u}\neq\m{0}$だから,$A$が正行列であることと併せて,$A\m{u}$は正ベクトルである.
よって,$\alpha\m{u}$は正ベクトルだから,$\alpha>0$と併せて$\m{u}$は正ベクトルであることが分かる.
ステップ4(固有値$\alpha$の重複度は1)
$\m{x},\m{y}\in\R^N$の標準内積を$\anb{\m{x},\m{y}}$で表す.
$A$の転置行列$A^T$も正行列だから,ステップ3までの結果が使えて,$A^T$の正固有値$\lambda$と,固有値$\lambda$に属する正の固有ベクトル$\m{v}$が存在する.このとき,
\begin{align*}(\alpha-\lambda)\anb{\m{v},\m{u}}
&=\anb{\m{v},\alpha\m{u}}-\anb{\lambda\m{v},\m{u}}
\\&=\anb{\m{v},A\m{u}}-\anb{A^T\m{v},\m{u}}
=0\end{align*}
であり,$\m{u}$, $\m{v}$は共に正ベクトルだから,$\anb{\m{v},\m{u}}>0$なので$\anb{\m{v},\m{u}}\neq0$である.よって,$\alpha=\lambda$が成り立つ.
ここで,固有値$\alpha$の固有空間の次元が1でないと仮定すると,固有値$\alpha$の固有ベクトル$\m{u}$, $\m{u}’$が存在して任意$a\in\R$に対して$\m{u}-a\m{u}’\neq\m{0}$となる.
$\m{u}-0\times\m{u}’=\m{u}$が正ベクトルであることとスカラー倍の連続性から,ある$k\in\R$が存在して$\m{u}-k\m{u}’$は成分の少なくとも1つが0の非負ベクトルとなり,仮定から$\m{u}-k\m{u}’$は零ベクトルではない.
一方,$A$が成分が正の行列であることから$A(\m{u}-k\m{u}’)=\alpha(\m{u}-k\m{u}’)$は正ベクトルとなって,$\m{u}-k\m{u}’$の成分に0があることに矛盾する.
よって,$\alpha$の固有空間の次元は1だから,$A$のジョルダン標準形の固有値$\alpha$に関するジョルダン細胞$J(\alpha)$の個数は1である.
もし,$J(\alpha)$の次数が2以上であれば,$\m{u}$が$A$の固有値$\alpha$に属する固有ベクトルであることから,$\m{w}\in\R^N$が存在して$A\m{w}=\alpha\m{w}+\m{u}$が成り立つ.よって,
\begin{align*}0<&\anb{\m{v},\m{u}}
=\anb{\m{v},A\m{w}-\alpha\m{w}}
\\=&\anb{A^T\m{v},\m{w}}-\alpha\anb{\m{v},\m{w}}
\\=&\anb{\lambda\m{v},\m{w}}-\alpha\anb{\m{v},\m{w}}
=0\end{align*}
となって矛盾するから,$J(\alpha)$の次数は1である.すなわち,$\alpha$の重複度は1である.
ステップ5(正の固有ベクトルが属する固有値は$\alpha$のみ)
$A$の固有値$\mu$が正の固有ベクトル$\m{v}’$を持つとする.ステップ4での$A^T$の固有値$\alpha$の固有ベクトル$\m{v}$を考えると
\begin{align*}(\mu-\alpha)\anb{\m{v},\m{v}’}
&=\anb{\m{v},\mu\m{v}’}-\anb{\alpha\m{v},\m{v}’}
\\&=\anb{\m{v},A\m{v}’}-\anb{A^T\m{v},\m{v}’}
=0\end{align*}
である.$\m{v}$, $\m{v}’$は共に正ベクトルだから,$\anb{\m{v},\m{v}’}>0$なので$\anb{\m{v},\m{v}’}\neq0$である.よって,$\alpha=\mu$が成り立つ.
ステップ6($\alpha$以外の固有値の絶対値)
$A$の$\alpha$と異なる任意の固有値$\beta$に対して,$|\beta|<\alpha$が成り立つ.
$\m{z}$を$A$の固有値$\beta$に属する固有ベクトルとする:$A\m{z}=\beta\m{z}$, $\m{z}\neq\m{0}$.
このとき,$A\m{z}=\beta\m{z}$の第$i$成分について,三角不等式を用いると
\begin{align*}\sum_{j=1}^{N}a_{ij}\abs{[\m{z}]_j}
&=\sum_{j=1}^{N}\abs{a_{ij}[\m{z}]_j}
\ge\abs{\sum_{j=1}^{N}a_{ij}[\m{z}]_j}\quad\dots(*)
\\&=\abs{[A\m{z}]_i}
=\abs{[\beta\m{z}]_i}
=|\beta|\abs{[\m{z}]_i}\end{align*}
だから,$A^T$の固有値$\alpha$に属する正の固有ベクトル$\m{v}$を用いると,
\begin{align*}\alpha\sum_{j=1}^{N}[\m{v}]_j\abs{[\m{z}]_j}
&=\sum_{j=1}^{N}[\alpha\m{v}]_j\abs{[\m{z}]_j}
=\sum_{j=1}^{N}[A^T\m{v}]_j\abs{[\m{z}]_j}
\\&=\sum_{j=1}^{N}\bra{\sum_{i=1}^Na_{ij}[\m{v}]_i}\abs{[\m{z}]_j}
\\&=\sum_{i=1}^{N}\bra{\sum_{j=1}^Na_{ij}\abs{[\m{z}]_j}}[\m{v}]_i
\\&\ge\sum_{i=1}^{N}\bra{|\beta|\abs{[\m{z}]_i}}[\m{v}]_i\quad\dots(**)
\\&=|\beta|\sum_{i=1}^{N}[\m{v}]_i\abs{[\m{z}]_i}\end{align*}
となる.$\m{z}\neq\m{0}$と$\m{v}$が正ベクトルであることから$\sum_{i=1}^N[\m{v}]_i\abs{[\m{z}]_i}\neq0$なので$\alpha\ge|\beta|$が従う.
よって,あとは$\alpha\neq|\beta|$を示せばよく,これを背理法により示す.
もし$\alpha=|\beta|$であれば,$(**)$で等号が成り立つから$(*)$でも等号が成り立つ.
一般に,複素数$\xi_1,\dots,\xi_n$に対して三角不等式$\abs{\sum_{k=1}^{n}\xi_k}\le\sum_{k=1}^{n}|\xi_k|$で等号が成り立つのは$\arg{\xi_1}=\dots=\arg{\xi_n}$の場合に限るから,$\m{z}$の各成分の偏角は全て等しい(ただし,偏角は$[-\pi,pi)$の範囲で定めている).
$\m{z}$の各成分の偏角を$\theta$とすると
\begin{align*}A(e^{-i\theta}\m{z})=e^{-i\theta}A\m{z}=e^{-i\theta}\beta\m{z}=\beta(e^{-i\theta}\m{z})\end{align*}
だから,$\beta$は固有ベクトル$e^{-i\theta}\m{z}$を持つ.
また,$A$は成分が正の行列だから$A(e^{-i\theta}\m{z})$は正ベクトルなので,$e^{-i\theta}\m{z}$は正ベクトルだからステップ5から$\beta=\alpha$となる.
これは仮定$\beta\neq\alpha$に矛盾するから$\alpha=|\beta|$は誤りで$\alpha>|\beta|$が従う.
以上で成分が正の行列に対するペロン-フロベニウスの定理が示されました.
参考文献
以下は参考文献です.
線型代数入門
[齋藤正彦 著/東京大学出版会]
線形代数の教科書として半世紀に渡って売れ続けている超ロングセラーの教科書です.
発刊されてから本書の内容の流れが線形代数の教科書のスタンダードとなったほど,日本の線形代数の指導にインパクトを与えた名著です.
その証拠に,著者の齋藤正彦氏は本書で日本数学会出版賞を受賞しています.
「線形代数をとりあえず使えるようにするための教科書」ではなく「線形代数を理解するための教科書」のため,論理的に非常に詳しく書かれているのが特徴です.
また,テキストのレベルとしては少なくとも理論系(特に数学系)の学部生であれば,確実に理解しておきたい程度のものとなっています.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの教科書|線型代数入門(齋藤正彦著,東京大学出版会)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.

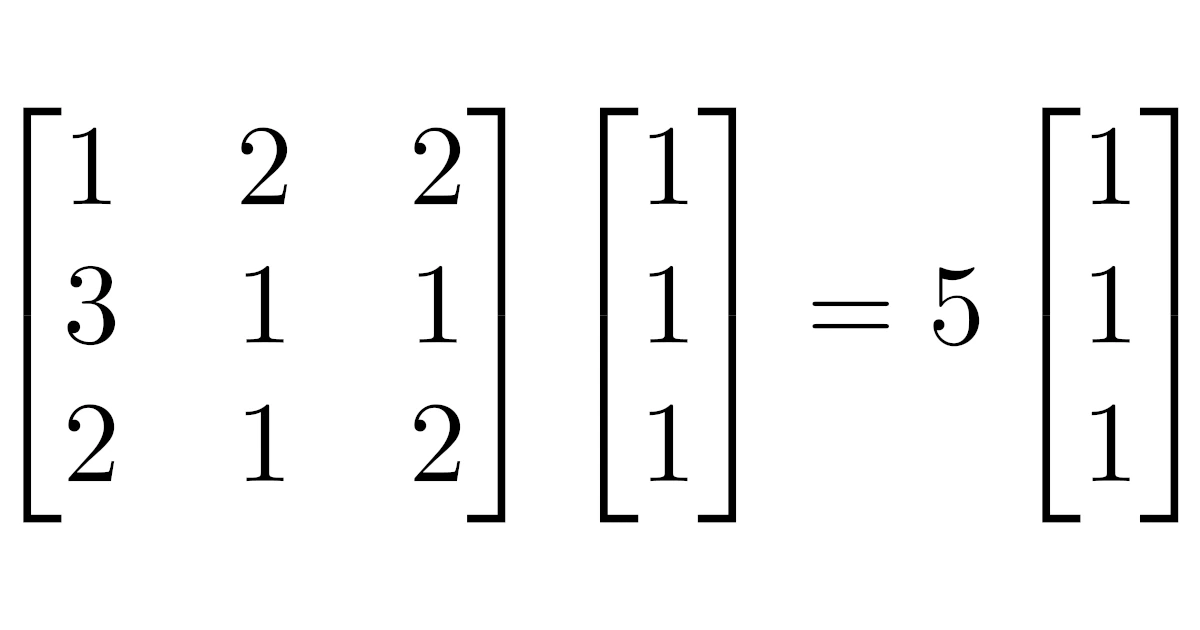

コメント