2変数関数$f$に対して$F(t)=\dint_{A}f(x,t)\,dx$で定まる関数$F$を微分するとき,微分$\frac{d}{dt}$と積分$\int$の順序交換をして
\begin{align*}F'(t)=\frac{d}{dt}\int_{A}f(x,t)\,dx=\int_{A}\frac{\partial f}{\partial t}(x,t)\,dx\end{align*}
と計算したいことがよくあります.
実は積分がルベーグ積分であれば,ルベーグの収束定理を用いて微分と積分の順序交換ができるための条件を導くことができます.
この記事では
- 微分と積分の順序交換条件の定理・具体例
- 微分と積分の順序交換条件の定理の証明
を順に解説します.
「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
微分と積分の順序交換条件の定理・具体例
微分と積分が順序交換可能であるための条件の定理を説明し,いくつか具体例を考えます.
具体例を考えたあとにルベーグの収束定理を確認し,主定理の証明をします.
偏導関数を上から評価する可積分関数がポイント
[微分と積分の順序交換条件]$A$を可測集合,$I$を開区間とする.$A\times I$上の可測関数$f(x,t)$は$t$について偏微分可能で,任意の$t\in I$に対して$f(\cdot,t)$は可積分であるとし,
\begin{align*}F(t)=\int_{A}f(x,t)\,dx\end{align*}
とおく.このとき,($t$によらない)ある$A$上の関数$g$が存在して,
- 任意の$t\in I$に対して$\abs{\frac{\partial f}{\partial t}(x,t)}\le g(x)$ a.e. $x\in A$
- $g$は$A$上可積分:$\int_{A}g(x)\,dx<\infty$
を満たすなら,$F$は$I$上微分可能で
\begin{align*}F'(t)=\int_{A}\frac{\partial f}{\partial t}(x,t)\,dx\end{align*}
が成り立つ.
結論の等式の$F$を書き直せば
\begin{align*}\frac{d}{dt}\int_{A}f(x,t)\,dx=\int_{A}\frac{\partial f}{\partial t}(x,t)\,dx\end{align*}
ですから,この定理は微分と積分の順序交換が可能であるための十分条件を述べる定理になっているわけですね.
関数$F$が微分できるかどうかを議論するためにはそもそも$F$が定義されていないといけませんから,「任意の$t\in I$に対して$f(\cdot,t)$は可積分である」という条件が前提にあるのは当たり前ですね.
なので,この定理を使う際のポイントは
- (ほとんど至るところ)$|\frac{\partial f}{\partial t}(x,t)|\le g(x)$を満たす関数$g$をとる
- $\int_{A}g(x)\,dx<\infty$を満たす
の2つを示すことですね.
具体例1($F(t)=\int_{[0,\infty)}e^{-tx^3}\,dx$)
$I=(0,\infty)$とする.関数$F:I\to\R$が
\begin{align*}F(t)=\int_{\R_{\ge0}}e^{-tx^3}\,dx\end{align*}
で定義できることを示し,$F$は微分可能で
\begin{align*}F'(t)=-\int_{\R_{\ge0}}x^3e^{-tx^3}\,dx\end{align*}
となることを示せ.ただし,$\R_{\ge0}=[0,\infty)$である.
変数変換すればガンマ関数を用いて$F$を表すこともできますが,ここでは微分と積分の順序交換により求めましょう.
関数$f:\R_{\ge0}\times I\to\R$を$f(x,t)=e^{-tx^3}$により定める.
関数$F:I\to\R$が定義できることの証明
任意に$t\in I$をとる.$f(\cdot,t)$は連続だから可測関数であり,任意の$x\in\R_{\ge0}$に対して
\begin{align*}|f(x,t)|\le\mathbb{I}_{[0,1]}(x)+x^2e^{-tx^3}\mathbb{I}_{(1,\infty)}(x)\end{align*}
が成り立つ.ただし,集合$X$に対して,$\mathbb{I}_{X}$は集合$X$の定義関数である.さらに
\begin{align*}&\int_{\R_{\ge0}}\bra{\mathbb{I}_{[0,1]}(x)+x^2e^{-tx^3}\mathbb{I}_{(1,\infty)}(x)}\,dx
\\&=1+\brc{-\frac{1}{3t}e^{-tx^3}}_{1}^{\infty}=1+\frac{1}{3t}e^{-t}<\infty\end{align*}
だから$f(\cdot,t)$は$\R_{\ge0}$上可積分.よって,関数$F:I\to\R$が定義できる.
微分と積分の順序交換により導関数$F’$を求める
任意に$\delta>0$を固定する.$f$は$t$について$(\delta,\infty)$上偏微分可能で,任意の$(x,t)\in\R_{\ge0}\times(\delta,\infty)$に対して
\begin{align*}\abs{\frac{\partial f}{\partial t}(x,t)}=\abs{-x^3e^{-tx^3}}\le x^3e^{-\delta x^3}\end{align*}
が成り立つ.さらに,
\begin{align*}\int_{\R_{\ge0}}x^3e^{-\delta x^3}\,dx&\le\int_{[0,1]}x^3\,dx+\int_{[1,\infty)}x^5e^{-\delta x^3}\,dx
\\&=\frac{1}{4}+\brc{-\frac{1}{3\delta}\bra{x^3+\frac{1}{\delta}}e^{-\delta x^3}}_{1}^{\infty}
\\&=\frac{1}{4}+\frac{1}{3\delta}\bra{1+\frac{1}{\delta}}e^{-\delta}<\infty\end{align*}
だから$x^3e^{-\delta x^3}$は$\R_{\ge0}$上可積分.
よって,[微分と積分の順序交換条件]の定理より,$F$は$(\delta,\infty)$上微分可能で,微分と積分の順序交換ができ,$\delta$によらず
\begin{align*}F'(t)=\int_{\R_{\ge0}}\frac{\partial f}{\partial t}(x,t)\,dx=-\int_{\R_{\ge0}}x^3e^{-tx^3}\,dx\quad\dots(*)\end{align*}
を得る.$\delta>0$は任意なので,$F$は$I$上微分可能で$(*)$を得る.
後半で微分可能性を示す際,最初から$I$全体で考えると上からの評価で$e$の負冪$e^{-\delta x^3}$を残せず上手くいかないため$(\delta,\infty)$で考えています.
この例のように指数関数を残すために,任意に$\delta>0$をとって$t$の下限を0から少し浮かせてから評価する方法はよく用いられるので知っておきたいところです.
具体例2($F(t)=\int_{\R}e^{-x^2}\cos{(tx)}\,dx$)
関数$F:\R\to\R$が
\begin{align*}F(t)=\int_{\R}e^{-x^2}\cos{(tx)}\,dx\end{align*}
で定義できて,微分方程式$F'(t)+\frac{t}{2}F(t)=0$が成り立つことを示し,$F$を求めよ.
関数$f:\R\times\R\to\R$を$f(x,t)=e^{-x^2}\cos{(tx)}$により定める.
関数$F:\R\to\R$が定義できることの証明
任意に$t\in\R$をとる.$f(\cdot,t)$は連続だから可測関数であり,任意の$x\in\R$に対して
\begin{align*}|f(x,t)|\le e^{-x^2}\end{align*}
が成り立つ.さらに,ガウス積分より
\begin{align*}\int_{\R}e^{-x^2}\,dx=\sqrt{\pi}<\infty\end{align*}
だから$f(\cdot,t)$は$\R$上可積分.よって,関数$F:\R\to\R$が定義できる.
微分と積分の順序交換により導関数$F’$を求める
$f$は$t$について$\R$上偏微分可能で,任意の$(x,t)\in\R\times\R$に対して
\begin{align*}\abs{\frac{\partial f}{\partial t}(x,t)}=\abs{-xe^{-x^2}\sin{(tx)}}\le|x|e^{-x^2}\end{align*}
が成り立つ.さらに,
\begin{align*}\int_{\R}|x|e^{-x^2}\,dx&=2\int_{[0,\infty)}xe^{-x^2}\,dx
\\&=2\brc{-\frac{1}{2}e^{-x^2}}_{0}^{\infty}=1<\infty\end{align*}
だから$|x|e^{-x^2}$は$\R$上可積分.
よって,[微分と積分の順序交換条件]の定理より,$F$は$\R$上微分可能で,微分と積分の順序交換ができ
\begin{align*}F'(t)=\int_{\R}\frac{\partial f}{\partial t}(x,t)\,dx=-\int_{\R}xe^{-x^2}\sin{(tx)}\,dx\end{align*}
を得る.
微分方程式$F'(t)+\frac{t}{2}F(t)=0$を導いて解く
部分積分より
\begin{align*}F'(t)&=\int_{\R}\bra{\frac{1}{2}e^{-x^2}}’\sin{(tx)}\,dx
\\&=\frac{1}{2}\bra{\brc{e^{-x^2}\sin{(tx)}}_{-\infty}^{\infty}-t\int_{\R}e^{-x^2}\cos{(tx)}\,dx}
\\&=-\frac{1}{2}t\int_{\R}e^{-x^2}\cos{(tx)}\,dx=-\frac{1}{2}tF(t)\end{align*}
が成り立つ.移項して微分方程式$F'(t)+\frac{t}{2}F(t)=0$が得られ,これは1階線形なので解ける.
$F(t)$の係数$\frac{t}{2}$の原始関数として$\frac{t^2}{4}$がとれるので,両辺に$e^{t^2/4}$をかけて
\begin{align*}&e^{t^2/4}F'(t)+\frac{t}{2}e^{t^2/4}F(t)=0
\iff\bra{e^{t^2/4}F(t)}’=0\end{align*}
が成り立つ.再びガウス積分より
\begin{align*}F(0)=\int_{\R}e^{-x^2}\,dx=\sqrt{\pi}\end{align*}
だから,両辺を$[0,t]$上で積分して,
\begin{align*}e^{t^2/4}F(t)-e^{0^2/4}F(0)=0
\iff F(t)=\sqrt{\pi}e^{-t^2/4}\end{align*}
を得る.
微分と積分の順序交換条件の定理の証明
ルベーグの収束定理のポイントを確認してから主定理を証明しましょう.
ルベーグの収束定理と使うための3つのポイント
ルベーグの収束定理は極限と積分の順序交換ができるための十分条件を述べた定理ですね.
[ルベーグの収束定理]$a\in\R$とし,$I$を$a$を元にもつ開区間とする.可測集合$A$と,$A$上の可測関数の族$\{f_t\}_{t\in I}$を考える.関数族$\{f_t\}_{t\in I}$が$A$上ほとんど至るところで各点収束し,($t$によらない)ある$A$上の関数$g$が存在して,
- 任意の$t\in I$に対して$|f(x,t)|\le g(x)$ a.e. $x\in A$
- $g$は$A$上可積分:$\int_{A}g(x)\,dx<\infty$
を満たすなら,極限$\lim_{t\to a}\int_{A}f_t(x)\,dx$が存在して
\begin{align*}\lim_{t\to a}\int_{A}f_t(x)\,dx=\int_{A}\lim_{t\to a}f_t(x)\,dx\end{align*}
が成り立つ.
ルベーグの収束定理を使う際には
- 関数列が(ほとんど至るところ)各点収束する
- (ほとんど至るところ)$|f_t|\le g$を満たす関数$g$をとる
- $\int_{A}g(x)\,dx<\infty$を満たす
の3つを示すことが大切なのでした.
標準的なルベーグの収束定理は関数列$\{f_n\}$に対するものですが,上記のように区間$I$を添え字集合とする関数族$\{f_t\}_{t\in I}$に対しても同様に成り立ちます.
証明のアイディアは平均値の定理
それでは,ルベーグの収束定理を用いて,微分と積分の順序交換できるための十分条件の定理を証明しましょう.
[微分と積分の順序交換条件(再掲)]$A$を可測集合,$I$を開区間とする.$A\times I$上の可測関数$f(x,t)$は$t$について偏微分可能で,任意の$t\in I$に対して$f(\cdot,t)$は可積分であるとし,
\begin{align*}F(t)=\int_{A}f(x,t)\,dx\end{align*}
とおく.このとき,($t\in I$によらない)ある$A$上の関数$g$が存在して,
- 任意の$t\in I$に対して$\abs{\frac{\partial f}{\partial t}(x,t)}\le g(x)$ a.e. $x\in A$
- $g$は$A$上可積分:$\int_{A}g(x)\,dx<\infty$
を満たすなら,$F$は$I$上微分可能で
\begin{align*}F'(t)=\int_{A}\frac{\partial f}{\partial t}(x,t)\,dx\end{align*}
が成り立つ.
任意に$t\in I$をとる.$f$は$t$について偏微分可能だから
\begin{align*}\lim_{h\to0}\frac{f(x,t+h)-f(x,t)}{h}=\frac{\partial f}{\partial t}(x,t)\end{align*}
が存在する.$t+h\in I$となる任意の$h\in\R$に対して,平均値の定理より,ある$\theta\in(0,1)$が存在して
\begin{align*}\abs{\frac{f(x,t+h)-f(x,t)}{h}}=\abs{\frac{\partial f}{\partial t}(x,t+\theta h)}\le g(x)\quad\mrm{a.e.}\ x\in A\end{align*}
が成り立つ.仮定より$g$は可積分だから,ルベーグの収束定理が適用できて
\begin{align*}F'(t)&=\lim_{h\to0}\frac{\int_{A}f(x,t+h)\,dx-\int_{A}f(x,t)\,dx}{h}
\\&=\lim_{h\to0}\int_{A}\frac{f(x,t+h)-f(x,t)}{h}\,dx
=\int_{A}\frac{\partial f}{\partial t}(x,t)\,dx\end{align*}
が成り立つ.
証明から分かるように,被積分関数の絶対値$\abs{\frac{f(x,t+h)-f(x,t)}{h}}$を評価するために平均値の定理を使うので,偏導関数$\frac{\partial f}{\partial t}(x,t)$を上から押さえる可積分関数$g$が存在すれば良いわけですね.

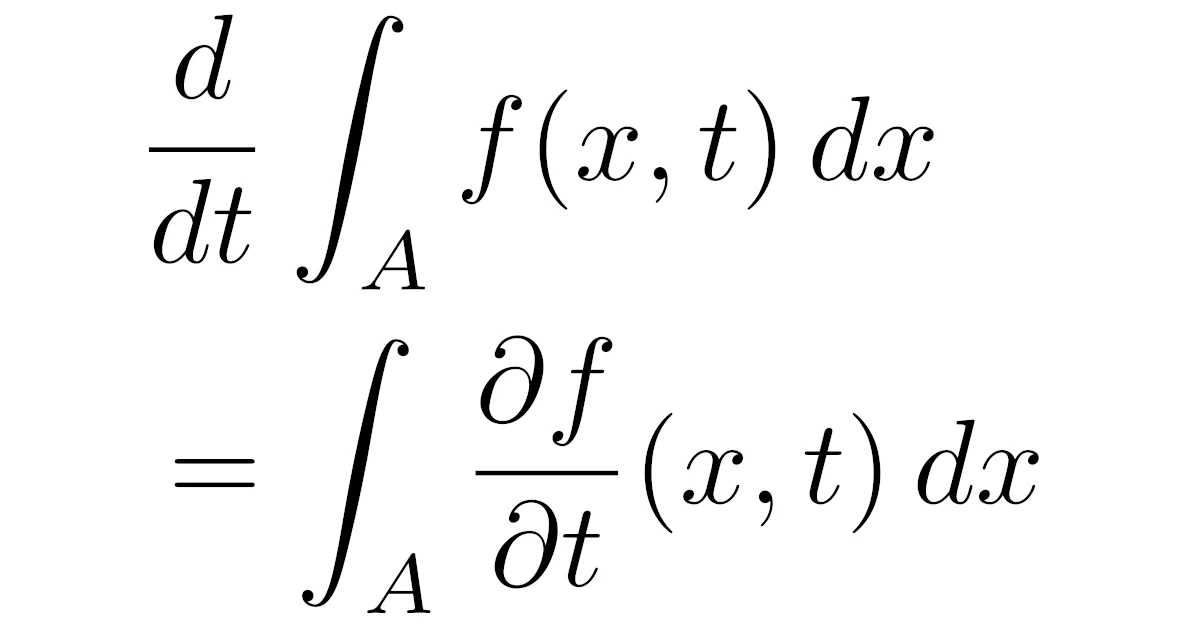


コメント