ルベーグの単調収束定理の例題と証明｜ルベーグ積分の重要定理

$A$上の関数列$\{f_n\}$が非負値可測単関数列で，$A$上で$0\le f_1\le f_2\le\dots$が成り立つとき，ルベーグ積分では

$\begin{align*}\lim_{n\to\infty}\int_{A}f_n(x)\,dx=\int_{A}\lim_{n\to\infty}f_n(x)\,dx\end{align*}$

と項別積分可能で，この定理を単関数列の項別積分定理と呼ぶのでした．

実はこの定理は$f_n$は単関数でなくても成り立つことが証明でき，この定理をルベーグの単調収束定理と呼びます．

この記事では

ルベーグの単調収束定理と具体例
ルベーグの単調収束定理の証明

を順に説明します．

以下ではルベーグ可測集合のことを単に「可測集合」と呼び，ルベーグ可測関数のことを単に「可測関数」と呼びます．

「ルベーグ積分の基本」の一連の記事

ルベーグ積分入門
1. 0 ルベーグ積分の基礎｜リーマン積分の先へ！積分の歴史から紹介

ルベーグ測度

ルベーグ可測関数とルベーグ積分

ルベーグ積分の性質と項別積分

ルベーグ積分の参考文献
1. ルベグ積分入門
2. ルベーグ積分と関数解析
ルベーグの単調収束定理と具体例
1. 具体例
2. 単関数列の項別積分定理との比較
ルベーグの単調収束定理の証明
1. 証明に重要な補題
2. ルベーグの単調収束定理の証明

ルベーグ積分の参考文献

以下はルベーグ積分に関するオススメの教科書です．

ルベグ積分入門

ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．

ルベーグ積分と関数解析

ルベーグ積分から更なるステップに進みたい人向けの教科書です．

ルベーグの単調収束定理と具体例

次の定理がこの記事のメインのルベーグの単調収束定理といいます．

［ルベーグの単調収束定理］可測集合$A$上の可測関数列$\{f_n\}$が$0\le f_1\le f_2\le\dots$を満たすとき，

$\begin{align*}\lim_{n\to\infty}\int_{A}f_n(x)\,dx=\int_{A}\lim_{n\to\infty}f_n(x)\,dx.\end{align*}$

が成り立つ．

条件$0\le f_1\le f_2\le\dots$は「関数列$\{f_n\}$が非負値かつ非減少（広義単調増加）である」といっても同じことですね．

ルベーグの単調収束定理は単に単調収束定理と呼ぶこともよくあります．

具体例

ルベーグの単調収束定理を用いると，次のような問題を解くことができます．

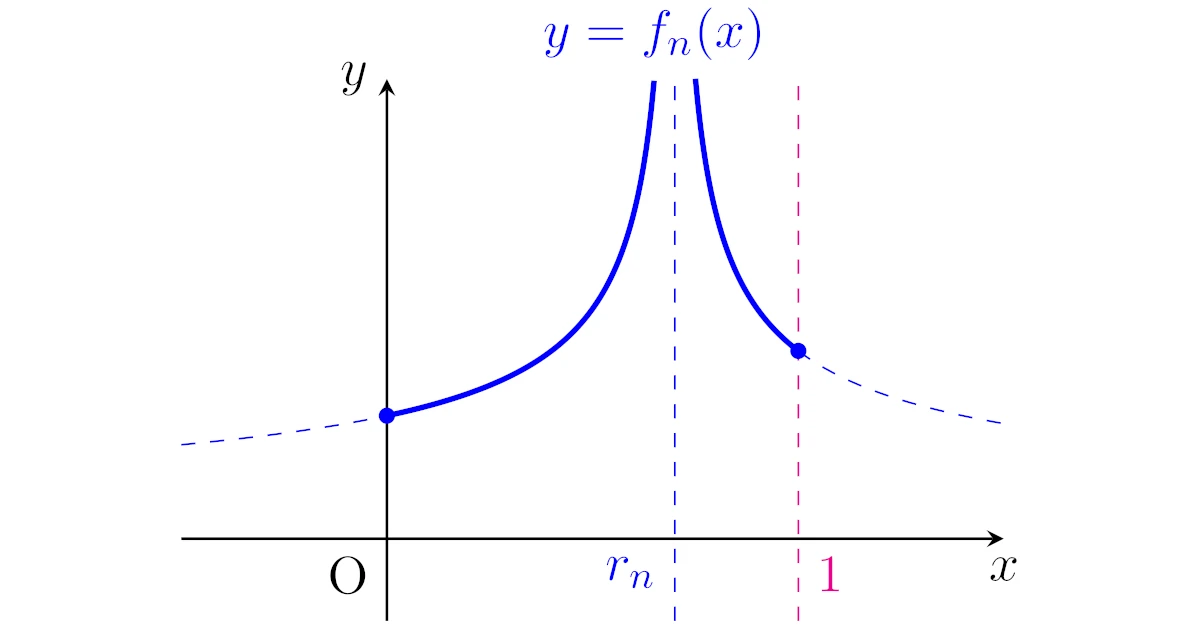
$\Q\cap[0,1]=\{r_1,r_2,\dots\}$とする．任意の$n\in\N$に対して，連続関数$f_n:[0,1]\to\R\cup\{\infty\}$を

$\begin{align*}f_n(x)=\frac{1}{2^n}\cdot\frac{1}{|x-r_n|^{1/2}}\end{align*}$

で定める．このとき，$f:=\sum\limits_{n=1}^{\infty}f_n$が$[0,1]$上ルベーグ可積分関数であることを示せ．

関数$f_n$は下図のようなグラフをもちますね．

各関数$f_n$は$r_n$で$\infty$を返す関数なので，これらの和$f$は閉区間$[0,1]$上の全ての有理数で$\infty$を返すにも関わらず，$[0,1]$上でルベーグ積分可能となっているところが面白い問題です．

$I:=[0,1]$とする．一般に連続関数は可測関数だから，各$f_n$は$I$上の非負値可測関数である．よって，関数列$\brb{\sum\limits_{n=1}^{N}f_n}$は非負値かつ非減少である．

よって，ルベーグの単調収束定理より

$\begin{align*}\int_{[0,1]}f(x)\,dx &=\int_{[0,1]}\sum_{n=1}^{\infty}f_n(x)\,dx =\sum_{n=1}^{\infty}\int_{[0,1]}f_n(x)\,dx \\&=\sum_{n=1}^{\infty}\frac{1}{2^n}\int_{[0,1]}\frac{1}{|x-r_n|^{1/2}}\,dx\end{align*}$

である（$\sum\limits_{n=1}^{\infty}=\lim\limits_{N\to\infty}\sum\limits_{n=1}^{N}$としてルベーグの単調収束定理を用いている）．また，各$n$に対して，

$\begin{align*}\int_{[0,1]}\frac{1}{|x-r_n|^{1/2}}\,dx \le\int_{[-1,1]}\frac{1}{|y|^{1/2}}\,dy =2\int_{[0,1]}\frac{1}{y^{1/2}}\,dy =4\end{align*}$

である（最初の不等号では変数変換$y=x-r_n$を施し，積分領域を大きくした）．よって，

$\begin{align*}\int_{[0,1]}f(x)\,dx=\sum_{n=1}^{\infty}\frac{4}{2^n}=4<\infty\end{align*}$

となるから，$f$は$[0,1]$上ルベーグ可積分関数である．

$\dint_{[0,1]}\dfrac{1}{|x-r_n|^{1/2}}\,dx$は$n$によらず一様に有界であり，$\dfrac{1}{2^n}$がかけられていることによって$\dint_{[0,1]}f_n(x)\,dx$は指数的に小さくなります．

そのため，先にルベーグ積分を計算してから無限和を考えることで有限の値に収束することが分かるわけですね．

単関数列の項別積分定理との比較

さて，次の定理を単関数列の項別積分定理というのでした．

［単関数列の項別積分定理］可測集合$A$上の可測単関数列$\{f_n\}$が$0\le f_1\le f_2\le\dots$を満たすとき，

$\begin{align*}\lim_{n\to\infty}\int_{A}f_n(x)\,dx=\int_{A}\lim_{n\to\infty}f_n(x)\,dx.\end{align*}$

が成り立つ．すなわち，$\{f_n\}$は項別積分可能である．

この定理は非負値関数のルベーグ積分の定義との相性が良く，また単関数近似定理とも相性が良いのですが，単関数列に対してしか適用できないという欠点があります．

一方でルベーグの単調収束定理は単関数でなくても適用できる定理となっており，単関数列の項別積分定理の上位互換となっていますね．

ルベーグの単調収束定理の証明

補題をひとつ証明してからルベーグの単調収束定理を証明しましょう．

証明に重要な補題

「補題」としていますが，本質的にはルベーグの単調収束定理と同じです．

［級数と積分の順序交換］可測集合$A$上の非負値可測関数列$\{f_n\}$に対して，

$\begin{align*}\sum_{n=1}^{\infty}\int_{A}f_n(x)\,dx=\int_{A}\sum_{n=1}^{\infty}f_n(x)\,dx\end{align*}$

が成り立つ．

級数の$\sum\limits_{n=1}^{\infty}$は$\lim\limits_{N\to\infty}\sum\limits_{n=1}^{N}$のことでしたから，極限$\lim$と積分$\dint$が順序交換されています．そのため，この補題も項別積分定理と呼ぶことができますね．

上で考えた具体例ではこの補題を直接用いたと考えても良いですね．

$f:=\sum\limits_{n=1}^{\infty}f_n$とする（各$f_n$は非負値だから$f:A\to\R_{\ge0}\cup\{\infty\}$として存在する）．このとき

$\begin{align*}\int_{A}f(x)\,dx=\sum_{n=1}^{\infty}\int_{A}f_n(x)\,dx\end{align*}$

を$\ge$と$\le$の両方の不等号が成り立つことから示す．

ステップ１（$\ge$の証明）

$f_n$は非負値だから，任意の$N\in\N$に対して

$\begin{align*}\int_{A}f(x)\,dx =&\int_{A}\sum_{n=1}^{\infty}f_n(x)\,dx \\\ge&\int_{A}\sum_{n=1}^{N}f_n(x)\,dx =\sum_{n=1}^{N}\int_{A}f_n(x)\,dx\end{align*}$

となるから，極限$N\to\infty$をとって

$\begin{align*}\int_{A}f(x)\,dx\ge\sum_{n=1}^{\infty}\int_{A}f_n(x)\,dx\end{align*}$

が成り立つ．

ステップ２（$\le$の証明）

単関数近似定理より，任意の$n\in\N$に対して

$\begin{align*}g_n^{(1)}\le g_n^{(2)}\le\dots,\quad \lim_{n\to\infty}f_n=g_n^{(k)}\end{align*}$

を満たす非負値可測単関数列$\{g_n^{(k)}\}_k$が存在する．さらに，$h_{\ell}:=\sum_{k=1}^{\ell}g_k^{(\ell)}$とする．

各$g_k^{(\ell)}$は非負値可測単関数だから，これらの和である$h_\ell$も非負値可測単関数である．$\{h_\ell\}$に単関数の項別積分定理を適用するために

$\begin{align*}h_1\le h_2\le\dots,\quad f=\lim_{\ell\to\infty}h_n\end{align*}$

を示す．

(i) $\{g_k^{(\ell)}\}$は$\ell$に関して非減少で，$g_{\ell+1}^{(\ell+1)}\ge0$だから

$\begin{align*}h_\ell=\sum_{k=1}^{\ell}g_k^{(\ell)}\le\sum_{k=1}^{\ell}g_k^{(\ell+1)}\le\sum_{k=1}^{\ell+1}g_k^{(\ell+1)}=h_{n+1}\end{align*}$

が成り立つ．

(ii) 任意に$\ell\in\N$をとると

$\begin{align*}f\ge\sum_{n=1}^{\ell}f_n\ge\sum_{n=1}^{\ell}g_n^{(\ell)}=h_\ell\end{align*}$

となるから，極限$\ell\to\infty$をとって$f\ge\lim\limits_{\ell\to\infty}h_\ell$が成り立つ．

また，$m\in\N$を$\ell\ge m$を満たすように任意にとると，$g_k^{(\ell)}$は非負値であることと併せて

$\begin{align*}h_\ell=\sum_{k=1}^{\ell}g_k^{(\ell)}\ge\sum_{k=1}^{m}g_k^{(\ell)}\end{align*}$

となるので，

$\begin{align*}\lim_{\ell\to\infty}h_\ell &=\lim_{m\to\infty}\lim_{\ell\to\infty}h_\ell \ge\lim_{m\to\infty}\lim_{\ell\to\infty}\sum_{k=1}^{m}g_k^{(\ell)} \\&\ge\lim_{m\to\infty}\sum_{k=1}^{m}\lim_{\ell\to\infty}g_k^{(\ell)} =\lim_{m\to\infty}\sum_{k=1}^{m}f_k =\sum_{k=1}^{\infty}f_k =f\end{align*}$

が成り立つ．よって，両方の不等式が示されたから$f=\lim\limits_{n\to\infty}h_n$が従う．

(i), (ii)より$\{h_n\}$に単関数の項別積分定理が適用できて

$\begin{align*}\int_{A}f(x)\,dx =&\lim_{\ell\to\infty}\int_{A}h_\ell(x)\,dx \le\lim_{\ell\to\infty}\int_{A}\sum_{n=1}^{\ell}f_n\,dx \\=&\lim_{\ell\to\infty}\sum_{n=1}^{\ell}\int_{A}f_n\,dx =\sum_{n=1}^{\infty}\int_{A}f_n\,dx\end{align*}$

が従う．

$f_1,\dots,f_\ell$それぞれ$\ell$段階目の単関数近似$g_1^{(\ell)},\dots,g_\ell^{(\ell)}$の和$h_\ell$を定義し，$\ell\to\infty$で

$\begin{align*}h_\ell\to f_1+f_2+\dots=f\end{align*}$

となることを証明し，$\{h_\ell\}$に単関数の項別積分定理を用いたわけですね．

ルベーグの単調収束定理の証明

それではルベーグの単調収束定理を証明しましょう．本質的にはいま証明した[級数と積分の順序交換]の補題と同じです．

［ルベーグの単調収束定理（再掲）］可測集合$A$上の可測関数列$\{f_n\}$が$0\le f_1\le f_2\le\dots$を満たすとき，

$\begin{align*}\lim_{n\to\infty}\int_{A}f_n(x)\,dx=\int_{A}\lim_{n\to\infty}f_n(x)\,dx.\end{align*}$

が成り立つ．

$m$をルベーグ測度とする．可測集合$A_n$ ($n=1,2,\dots$)と$B$を

$\begin{align*}A_n:=\set{x\in A}{f_n(x)=\infty},\quad B:=\bigcup_{n=1}^{\infty} A_n\end{align*}$

で定めると，$A_n\subset A_{n+1}$ ($n=1,2,\dots$)なので$m(B)=\lim\limits_{n\to\infty}m(A_n)$が成り立つ．

以下，$m(B)=0$の場合と$m(B)>0$の場合に分けて示す．

ステップ１（$m(B)=0$の場合）

$m(B)=0$の場合を考える．$A\setminus B$で

$\begin{align*}g_1:=f_1,\quad g_n:=f_n-f_{n-1}\ (n=1,2,\dots)\end{align*}$

と定めると，$\{f_n\}$が非減少な非負値可測関数列だから，$g_k$は非負値可測関数である．また，$f_n=\sum\limits_{k=1}^{n}g_k$となる．

よって，$\{g_k\}$に[級数と積分の順序交換]の補題を適用して

$\begin{align*}&\int_{A\setminus B}\lim_{n\to\infty}f_n(x)\,dx =\sum_{k=1}^{\infty}\int_{A\setminus B}g_k(x)\,dx \\&=\lim_{n\to\infty}\sum_{k=1}^{n}\int_{A\setminus B}g_k(x)\,dx =\lim_{n\to\infty}\int_{A\setminus B}\sum_{k=1}^{n}g_k(x)\,dx \\&=\lim_{n\to\infty}\int_{A\setminus B}f_n(x)\,dx\end{align*}$

が従う．よって，$m(B)=0$と併せて

$\begin{align*}\int_{A}\lim_{n\to\infty}f_n(x)\,dx=\lim_{n\to\infty}\int_{A}f_n(x)\,dx\end{align*}$

を得る．

ステップ２（$m(B)>0$の場合）

$m(B)>0$の場合を考える．ある$N\in\N$が存在して，

$\begin{align*}B':=m(\set{x\in A}{f_N(x)=\infty})>0\end{align*}$

が成り立つ．また，

$\begin{align*}\lim_{n\to\infty}\int_{A}f_n(x)\,dx\ge\int_{A}f_N(x)\,dx,\quad \int_{A}\lim_{n\to\infty}f_n(x)\,dx\ge\int_{A}f_N(x)\,dx\end{align*}$

であり，

$\begin{align*}\int_{A}f_N(x)\,dx\ge\int_{B'}f_N(x)\,dx=m(B')\cdot\infty=\infty\end{align*}$

だから，両辺とも$\infty$なので等号が成り立つ．

場合分けで$m(B)>0$の場合を除外した理由は，$B$では$g_n=f_n-f_{n-1}$が$\infty-\infty$となって$g_n$が定義できないためです．

本質的なイメージは$f_n=\sum\limits_{k=1}^{n}g_k$から級数と積分の順序交換を適用するというところです．

つまり，$\{f_n\}$は非減少なので$f_{n-1}$から$f_n$で増えた分$g_n$を足していけば，非負値可測関数の級数となり［級数と積分の順序交換］の補題が適用できるという発想ですね．