実数値確率変数$X$に対して,$X^n$($n\in\N$)の期待値$E[X^n]$を$X$の$n$次モーメントといいます.
1次モーメント$E[X]$はよく知られているように$X$の平均を表しますし,加えて2次モーメント$E[X^2]$も分かると$X$の分散を求めることができますね.このように,モーメントは確率変数の性質を捉える上で重要な量です.
また,$e^{tX}$の期待値$E[e^{tX}]$を$X$の積率母関数またはモーメント母関数などといい,$M(t)=E[e^{tX}]$とすると
となって,$t=0$を代入することで$n$次モーメントが$E[X^n]=\dfrac{d^nM}{dt^n}(0)$により求められます.
しかし,この式変形では微分$\dfrac{d^n}{dt^n}$と期待値$E$の順序を途中で交換しており,これが本当に正しいのかどうか数学的にはきちんと議論する必要があります.
そこで,この記事では積率母関数が存在すれば,この順序交換がきちんと正当化できることをルベーグの収束定理から証明します.
積率母関数
この記事では実数値確率変数を$X$とします.
積率母関数の定義
まずは積率母関数の定義を確認しましょう.
確率空間$(\R,\mathcal{B}(\R),P)$上の実数値確率変数$X$を考える.$t\in\R$に対して
が存在すれば,これを$t$でのXの積率母関数(またはモーメント母関数)という.
ただし,$\mathcal{B}(\R)$は$\R$のボレル集合族である.
$X$の確率密度関数を$f$とすれば
と表すこともできるので,確率空間をよく知らない場合はこれを$t$の積率母関数の定義と思って構いません.
以下では特に断りませんが,$X$は確率空間$(\R,\mathcal{B}(\R),P)$上の実数値確率変数とします.
積率母関数の導関数
積率母関数の導関数について次が成り立ちます.この記事では,この定理を示すことを目標とします.
[積率母関数の導関数] 確率変数$X$に対して,ある開区間$I$上で積率母関数$M(t)=E[e^{tX}]$が存在すれば,$M\in C^{\infty}(I)$かつ任意の$n\in\N$に対して$E[X^{n}e^{tX}]<\infty$であって
が成り立つ.
$0\in I$を満たす場合には,$t=0$とすることで次の系が成り立ちますね.
[積率母関数とモーメント] $0$の近傍で積率母関数$M$が存在する確率変数$X$に対して,$M\in C^{\infty}(I)$かつ任意の$n\in\N$に対して$E[X^{n}]<\infty$であって
が成り立つ.
よって,積率母関数$M$が得られていれば,$n$階導関数$\dfrac{d^nM}{dt^n}$を求めて$t=0$を代入すれば$n$次モーメント$E[X^n]$が得られますね.
ルベーグの収束定理
関数列$\{f_s\}$について
と極限と積分の順序交換ができるとき,$\{f_s\}$は項別積分可能であるといいます.
測度論においてルベーグの収束定理は項別積分可能であるための十分条件を述べたものとして重要です.この記事で使われる形で書いておきましょう.
[ルベーグの収束定理] $I$は$0$を含む開区間とし,$A\subset\R$はルベーグ可測集合とする.$A$上のルベーグ可測関数族$\{f_s\}_{s\in I}$が次の2条件を満たすとする.
- $A$上ほとんど至るところで$\lim\limits_{s\to 0}f_{s}$が存在する.
- あるルベーグ可積分関数$g:A\to\R$が存在して,任意の$s\in I$に対して,$A$上ほとんど至るところで$|f_{s}|\le g$が成り立つ.
このとき,$\lim\limits_{s\to 0}f_{s}$は$A$上ルベーグ可積分で
が成り立つ.
ルベーグの収束定理は一般の測度空間でも成り立ちます.この記事では,測度空間$(\R,\mathbb{B}(\R),P)$に対して用います.
2つ目の条件の$g$はパラメータ$s$に依らない関数として存在しなければならないことが大切です.
積率母関数の導関数の定理の証明
それでは上記の[積率母関数の導関数]の定理の証明に移ります.
証明の方針
[積率母関数の導関数]の定理を示すために,ルベーグの収束定理をどのように用いるか簡単に方針を説明しておきます.
積率母関数$M$の定義は
だったので,
となりますね($\theta\in(0,1)$).
最後の等式では平均値の定理を用いています.
また,
ですから,$(*)$と$(**)$は$\lim\limits_{h\to0}$と$\dint_{\R}$の順序交換をしたものになっています.
よって,ルベーグの収束定理を適用することができれば,[積率母関数の導関数]の定理の$n=1$での等式が成り立つことになりますね.
証明
それでは証明しましょう.
[積率母関数の導関数(再掲)] 確率変数$X$に対して,ある開区間$I$上で積率母関数$M(t)=E[e^{tX}]$が存在すれば,$M\in C^{\infty}(I)$かつ任意の$n\in\N$に対して$E[X^{n}e^{tX}]<\infty$であって
が成り立つ.
$I=(a,b)$とする.任意に$t\in I$をとり,$t$で$M$が微分可能であることを示す.
$c:=\frac{a+t}{2}$, $d:=\frac{b+t}{2}$とする.平均値の定理より,$t+h\in(c,d)$なる任意の$h\in\R$に対して,ある$\theta\in(0,1)$が存在して
が成り立つ.
いま,$\R$上至るところで
である(上記のルベーグの収束定理の1つ目の条件に相当).$t+\theta h\in(c,d)$より
だから,ある$R>0$が存在して
- $x<-R$なら$|xe^{(t+\theta h)x}|<e^{cx}$
- $R<x$なら$|xe^{(t+\theta h)x}|<e^{dx}$
が成り立つ.よって,$g:\R\to\R$を
とすると,$t+h\in(c,d)$なる任意の$h\in\R$に対して$\abs{xe^{(t+\theta h)x}}\le g(x)$が成り立つ.
また,$I$上で積率母関数が存在することより$E[e^{cX}]$, $E[e^{dX}]$は存在するから,
となって,$g$は$\R$上可積分であることが分かる(上記のルベーグの収束定理の2つ目の条件に相当).
以上より,ルベーグの収束定理が適用できて
が従う.$t\in I$は任意だったから,$M$は$I$上微分可能で$n=1$の場合の等式が得られた.
$n\ge2$の場合も同様に,ある$R_{n}>0$が存在して
- $x<-R_{n}$なら$|x^{n}e^{(t+\theta h)x}|<e^{cx}$
- $R_{n}<x$なら$|x^{n}e^{(t+\theta h)x}|<e^{dx}$
が成り立つので,帰納的に$M\in C^{\infty}(I)$と任意の$n\in\N$に対して等式が従う.

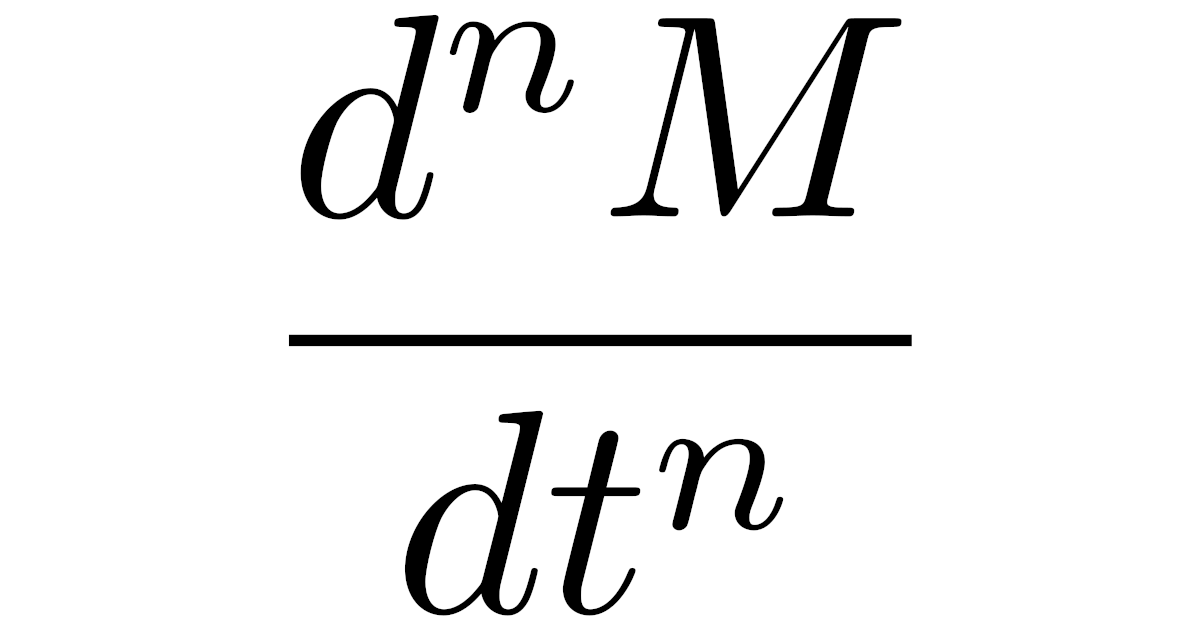
コメント