ルベーグ可測集合族は完全加法族｜和集合・共通部分の可測性

ルベーグ積分の基本
2022.07.06
ルベーグ積分の基本

ルベーグ外測度$m^{*}$の定義域をルベーグ可測集合族$\mathcal{L}$に制限してできる写像$m$をルベーグ測度というのでした．

ルベーグ測度$m$はルベーグ積分において本質的に重要な役割を果たすので，ルベーグ測度$m$の定義域である$\mathcal{L}$の性質も整理しておく必要があります．

その中でも「$\mathcal{L}$が完全加法族である」という性質はルベーグ測度$m$のベースとなっています．

この記事では

  • ルベーグ可測集合の復習
  • ルベーグ可測集合の和集合と共通部分
  • ルベーグ可測集合族$\mathcal{L}$と完全加法族

を順に説明します．

以下ではルベーグ可測集合のことを単に「可測集合」と呼びます．ルベーグ外測度を$m^{*}$で表し，単に「外測度」と呼びます．

「ルベーグ積分の基本」の一連の記事

  1. ルベーグ積分入門
    1. 0 ルベーグ積分の基礎｜リーマン積分の先へ！積分の歴史から紹介
  1. ルベーグ測度
    1. 1 外測度とは何か？集合の「長さ」の測り方
    2. 2 外測度の本質的に重要な５つの性質
    3. 3 可測集合の定義とルベーグ測度の定義
    4. 4 可測集合の基本性質のまとめと完全加法族 (今の記事)
    5. 5 区間・開集合・閉集合の可測性とボレル集合族
    6. 6 ルベーグ測度の本質的に重要な４つの性質
  1. ルベーグ可測関数とルベーグ積分
    1. 7 可測関数の定義・具体例・必要十分条件
    2. 8 可測関数からなる関数の可測性を証明する
    3. 9 単関数の定義と可測単関数のルベーグ積分
    4. 10 可測関数を単関数列で近似する重要定理
    5. 11 一般の可測関数にルベーグ積分を定義する
  1. ルベーグ積分の性質と項別積分
    1. 12 非負値可測関数のルベーグ積分の基本性質
    2. 13 単関数列の項別積分定理の考え方・応用・証明
    3. 14 ルベーグの単調収束定理と具体例と証明
    4. 15 ファトゥの補題の使い方を例題から理解する
    5. 16 ルベーグの収束定理の応用例を理解する
    6. 17 リーマン積分の関係とルベーグ積分の計算例

ルベーグ積分の参考文献

以下はルベーグ積分に関するオススメの教科書です．

ルベグ積分入門

ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．

ルベーグ積分と関数解析

ルベーグ積分から更なるステップに進みたい人向けの教科書です．

ルベーグ可測集合の復習

可測集合の定義を確認しましょう．

集合$A\subset\R$が可測集合であるとは，任意の$X\subset\R$に対して

    \begin{align*}m^{*}(X)=m^{*}(X\cap A)+m^{*}(X\cap A^c)\quad\dots(\star)\end{align*}

を満たすことをいう．ここに，$A^c$は$\R$における$A$の補集合である．

また，ルベーグ可測集合全部の族をルベーグ可測集合族という．

外測度$m^{*}$の劣加法性から不等式

    \begin{align*}m^{*}(X)\le m^{*}(X\cap A)+m^{*}(X\cap A^c)\end{align*}

は常に成り立ち，また$m^{*}(X)=\infty$なら逆向き$\ge$の不等式も常に成り立ちます．

これらのことから，次の可測集合であるための必要十分条件を思い出しておきましょう（この記事でも度々用います）．

集合$A\subset\R$に対して，次は同値である．

  • $A$は可測集合である．
  • $m^{*}(X)<\infty$なる任意の$X\subset\R$に対して$m^{*}(X)\ge m^{*}(X\cap A)+m^{*}(X\cap A^c)$が成り立つ．

ルベーグ可測集合の和集合と共通部分

ここでは可測集合の基本性質として，補集合・和集合・共通部分・差集合の可測性を考えましょう．

ルベーグ可測集合の補集合

可測集合の補集合は可測集合です．

［補集合］可測集合$A\subset\R$に対して，$A^c$は可測集合である．

任意に$X\subset\R$をとる．$A$は可測集合だから，可測集合の定義より

    \begin{align*}m^{*}(X) =&m^{*}(X\cap A)+m^{*}(X\cap A^c) \\=&m^{*}(X\cap(A^c)^c)+m^{*}(X\cap A^c)\end{align*}

が成り立つ．よって，$A^c$は可測集合である．

ルベーグ可測集合の和集合

２つの可測集合の和集合・共通部分はともに可測集合です．

［和集合］可測集合$A,B\subset\R$に対して，$A\cup B$は可測集合である．

任意に$m^{*}(X)<\infty$なる$X\subset\R$をとる．このとき

    \begin{align*}m^{*}(X)\ge m^{*}(X\cap (A\cup B))+m^{*}(X\cap (A\cup B)^c)\end{align*}

が成り立つことを示せばよい．

$A$は可測集合だから，可測集合の定義より

    \begin{align*}m^{*}(X)=m^{*}(X\cap A)+m^{*}(X\cap A^c)\end{align*}

が成り立つ．また，$B$は可測集合だから，可測集合の定義より

    \begin{align*}m^{*}(X\cap A^c) =&m^{*}((X\cap A^c)\cap B)+m^{*}((X\cap A^c)\cap B^c) \\=&m^{*}(X\cap A^c\cap B)+m^{*}(X\cap(A\cup B)^c)\end{align*}

が成り立つ．ただし，２つ目の等号では第２項目にド・モルガンの法則を用いている．よって，

    \begin{align*}m^{*}(X)=m^{*}(X\cap A)+m^{*}(X\cap A^c\cap B)+m^{*}(X\cap(A\cup B)^c)\end{align*}

が成り立つから，あとは$m^{*}(X\cap A)+m^{*}(X\cap A^c\cap B)\ge m^{*}(X\cap (A\cup B))$を示せばよい．

一般に集合$P$, $Q$, $R$に対して，分配法則

  • $P\cap (Q\cup R)=(P\cap Q)\cup (P\cap R)$
  • $P\cup (Q\cap R)=(P\cup Q)\cap (P\cup R)$

が成り立つことを用いると，

    \begin{align*}&(X\cap A)\cup(X\cap A^c\cap B) \\=&X\cap (A\cup(A^c\cap B)) =X\cap ((A\cup A^c)\cap(A\cup B)) \\=&X\cap\R\cap(A\cup B) =X\cap(A\cup B)\end{align*}

だから，外測度$m^{*}$の劣加法性より

    \begin{align*}m^{*}(X\cap A)+m^{*}(X\cap A^c\cap B)\ge m^{*}(X\cap (A\cup B))\end{align*}

が示された．

帰納的に$A_1,A_2,\dots,A_n\in\mathcal{L}$に対して，$\bigcup\limits_{k=1}^{n}A_k\in\mathcal{L}$が成り立つことも分かりますね．

ルベーグ可測集合の共通部分

上で示した命題［和集合］と命題［補集合］を用いると，２つの可測集合の共通部分も可測集合であることが直ちに示されます．

［共通部分］可測集合$A,B\subset\R$に対して，$A\cap B$は可測集合である．

$A,B$は可測集合だから，命題［補集合］を用いると$A^c,B^c$は可測集合なので，命題［和集合］より$A^c\cup B^c$は可測集合である．

再び命題［補集合］を用いると$(A^c\cup B^c)^c$は可測集合であり，ド・モルガンの定理より

    \begin{align*}(A^c\cup B^c)^c=A\cap B\end{align*}

が従う．よって，$A\cap B$は可測集合である．

帰納的に$A_1,A_2,\dots,A_n\in\mathcal{L}$に対して，$\bigcap\limits_{k=1}^{n}A_k\in\mathcal{L}$が成り立つことも分かりますね．

さらに，差集合$A\setminus B$は$A\cap B^c$であることから，次も成り立ちますね．

［差集合］可測集合$A,B\subset\R$に対して，$A\setminus B$は可測集合である．

差集合の定義は$A\setminus B=A\cap B^c$である．

$B$は可測集合だから命題［補集合］を用いると$B^c$は共通部分であり，さらに$A$が可測集合であることと系［共通部分］を併せて$A\cap B^c$は可測集合である．

ルベーグ可測集合族$\mathcal{L}$と完全加法族

命題［和集合］は有限個の可測集合の和集合についての性質でしたが，実は可算無限個の可測集合であっても和集合は可測集合となります．

可測集合$A_1,A_2,\dots\subset\R$に対して$\bigcup\limits_{n=1}^{\infty}A_n$は可測集合である．

この性質を「ルベーグ可測集合族は$\R$の完全加法族である」といいます（この記事の最後を後述）．

補題

上の定理の証明のために，次の補題を用意しておきます．

可測集合$A_1,A_2,\dots\subset\R$が互いに素（$i\neq j$なら$A_i\cap A_j=\emptyset$）なら，任意の$X\subset\R$と$n\in\N$に対して

    \begin{align*}m^{*}\bra{X\cap B_n}=\sum_{k=1}^{n}m^{*}(X\cap A_k)\end{align*}

が成り立つ．ただし，$B_n=\bigcup\limits_{k=1}^{n}A_k$（$n\in\N$）である．

数学的帰納法により示す．$n=1$のときは

    \begin{align*}X\cap B_n=X\cap B_1=X\cap A_1=X\cap A_n\end{align*}

だから$m^{*}(X\cap B_n)=\sum\limits_{k=1}^{n}m^{*}(X\cap A_k)$が成り立つ．

ある$n$に対して成り立つと仮定する．$A_{n+1}$は可測集合だから

    \begin{align*}m^{*}(X\cap B_{n+1}) &=m^{*}((X\cap B_{n+1})\cap A_{n+1}) \\&\quad+m^{*}((X\cap B_{n+1})\cap A_{n+1}^c)\end{align*}

である．いま$A_1,A_2,\dots,A_{n+1}$は互いに素と仮定しているので$B_{n+1}\cap A_{n+1}=A_{n+1}$, $B_{n+1}\cap A_{n+1}^c=B_{n}$だから，帰納法の仮定と併せると

    \begin{align*}m^{*}(X\cap B_{n+1}) &=m^{*}(X\cap A_{n+1})+m^{*}(X\cap B_{n}) \\&=m^{*}(X\cap A_{n+1})+\sum_{k=1}^{n}m^{*}(X\cap A_k) \\&=\sum_{k=1}^{n+1}m^{*}(X\cap A_k)\end{align*}

を得る．よって，$n+1$でも成り立つ．

定理の証明

この補題を用いて，上の定理を証明しましょう．

（再掲）可測集合$A_1,A_2,\dots\subset\R$に対して$\bigcup\limits_{n=1}^{\infty}A_n$は可測集合である．

$A=\bigcup\limits_{n=1}^{\infty}A_n$, $B_n=\bigcup\limits_{k=1}^{n}A_k$（$n\in\N$）とおく．命題［和集合］より，任意の$n\in\N$に対して$B_n$は可測集合である．

$A$が可測集合であることを２ステップで示す．

ステップ１

$A_1,A_2,\dots$が互いに素の場合に示す．任意に$m^{*}(X)<\infty$なる$X\subset\R$をとる．$B_n$の可測性より

    \begin{align*}m^{*}(X)=m^{*}(X\cap B_n)+m^{*}(X\cap B_n^c)\end{align*}

が成り立つ．また，補題より

    \begin{align*}m^{*}(X\cap B_n)=\sum_{k=1}^{n}m^{*}(X\cap A_k)\end{align*}

が成り立ち，$B_n\subset A$より$X\cap B_n^c\supset X\cap A^c$だから，外測度$m^{*}$の単調性より

    \begin{align*}m^{*}(X\cap B_n^c)\ge m^{*}(X\cap A^c)\end{align*}

が成り立つ．よって

    \begin{align*}m^{*}(X)\ge \sum_{k=1}^{n}m^{*}(X\cap A_k)+m^{*}(X\cap A^c)\end{align*}

が成り立つから，両辺で$n\to\infty$とすると

    \begin{align*}m^{*}(X) &\ge\sum_{k=1}^{\infty}m^{*}(X\cap A_k)+m^{*}(X\cap A^c) \\&\ge m^{*}\bra{\bigcup_{k=1}^{\infty}(X\cap A_k)}+m^{*}(X\cap A^c) \\&=m^{*}\bra{X\cap A}+m^{*}(X\cap A^c)\end{align*}

を得る．ただし，２つ目の不等号では第１項で外測度$m^{*}$の劣加法性を用いた．よって，$A$は可測集合である．

ステップ２

一般の$A_1,A_2,\dots$に対して成り立つことを示す．

$A’_1=A_1$, $A’_n=A_n\setminus B_{n-1}$ ($n=2,3,\dots$)とおくと，$A’_1,A’_2,\dots$は互いに素であり，命題［差集合］より$A’_1,A’_2,\dots$は可測集合である．

よって，ステップ１より$\bigcup\limits_{n=1}^{\infty}A’_n$は可測集合である．

さらに，$\bigcup\limits_{n=1}^{\infty}A_n=\bigcup\limits_{n=1}^{\infty}A’_n$だから$\bigcup\limits_{n=1}^{\infty}A_n$は可測集合である．

可算無限個の共通部分

可算無限個の和集合ではなく無限個の共通部分であっても，同様に可測集合となります．

可測集合$A_1,A_2,\dots\subset\R$に対して$\bigcap\limits_{n=1}^{\infty}A_n$は可測集合である．

ド・モルガンの定理より

    \begin{align*}\bra{\bigcap\limits_{n=1}^{\infty}A_n}^c=\bigcup\limits_{n=1}^{\infty}A_n^c\end{align*}

である．命題［補集合］より$A_1^c,A_2^c,\dots$も可測集合だから，$\mathcal{L}$が完全加法族であることより$\bigcup\limits_{n=1}^{\infty}A_n^c$は可測集合である．

よって，$\bigcap\limits_{n=1}^{\infty}A_n$は可測集合である．

可測空間と完全加法族

実は測度論において可測空間と呼ばれる基本的な概念があります．

集合$\Omega$と$\Omega$の部分集合の族$\mathcal{F}$が３条件

  1. $\Omega\in\mathcal{F}$
  2. $A\in\mathcal{F}\Ra A^c\in\mathcal{F}$
  3. $A_1,A_2,\dots\in\mathcal{F}\Ra \bigcup\limits_{n=1}^{\infty}A_n\in\mathcal{F}$

を満たすとき，組$(\Omega,\mathcal{F})$を可測空間（measurable space）という．また，$\mathcal{F}$を$\Omega$の完全加法族（completely additive class）という．

完全加法族は$\sigma$-加法族，$\sigma$-代数などと呼ばれることもよくあります．

ルベーグ可測集合族を$\mathcal{L}$と表すと，

  1. 実数全部の集合$\R$は可測集合だったから，$\R\in\mathcal{L}$
  2. 命題［補集合］から，$A\in\mathcal{L}\Ra A^c\in\mathcal{L}$
  3. いま示した定理から，$A_1,A_2,\dots\in\mathcal{L}\Ra \bigcup\limits_{n=1}^{\infty}A_n\in\mathcal{L}$

が成り立つので，組$(\R,\mathcal{L})$は可測空間であり，$\mathcal{L}$は$\R$の完全加法族であることが分かりますね．

可測空間（と測度空間）について詳しくは以下の記事を参照してください．

可測空間と測度空間｜直感的な考え方で定義・具体例を解説
測度論の基本的な空間として「可測空間」「測度空間」があります．この記事では，これらの直感的な考え方をたどりながら，定義と具体例を丁寧に解説していきます．
math-note.xyz

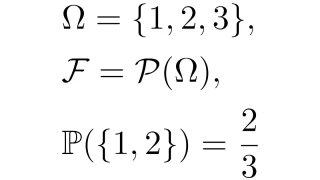
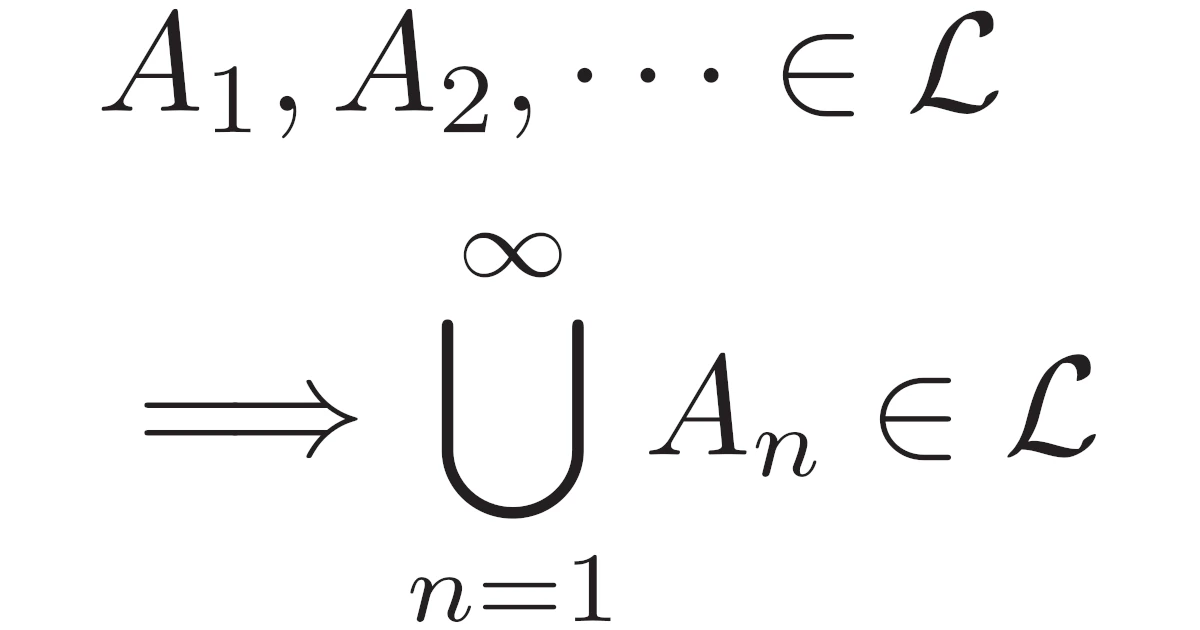
コメント