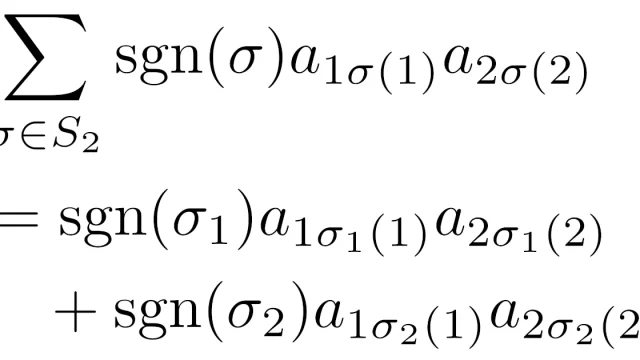 線形代数学の基本
線形代数学の基本 行列式の定義と具体例|置換の符号(偶置換・奇置換)から解説
正方行列Aの行列式|A|は,|A|=0であるか否かを見ることでAの正則性を判定できる便利なものです.行列式は置換を用いて定義されることが多く,この記事でも置換の符号を定義して行列式の定義と具体例を説明しています.
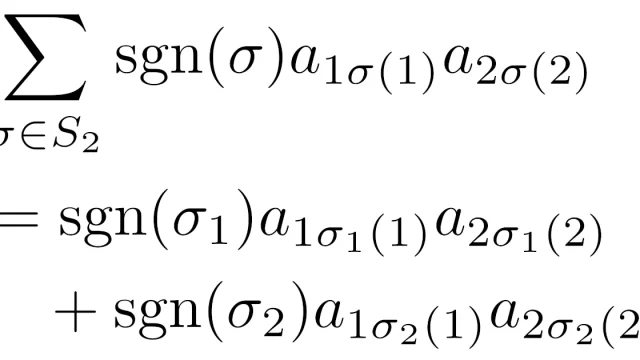 線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本 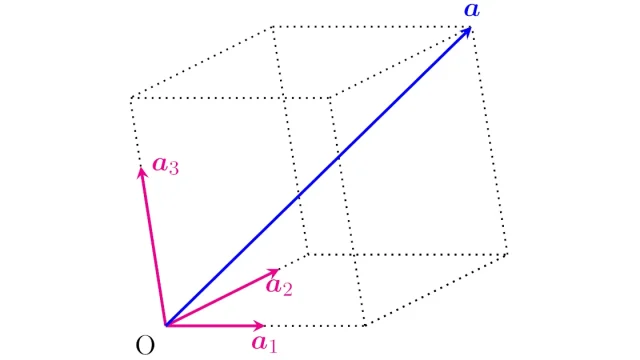 線形代数学の基本
線形代数学の基本 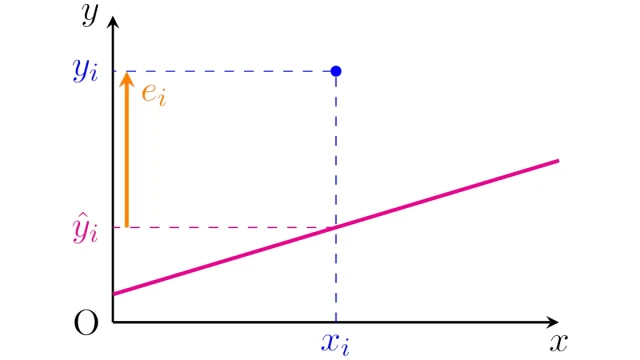 統計学
統計学  コマンド
コマンド 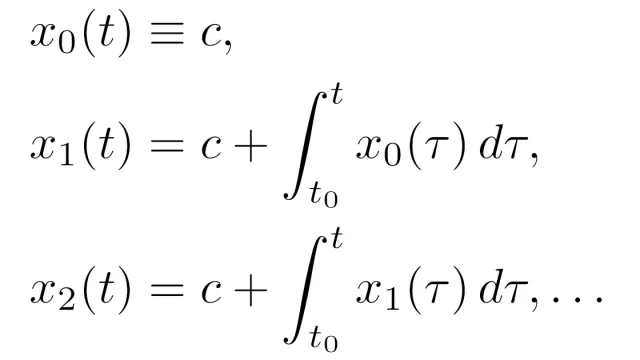 常微分方程式
常微分方程式 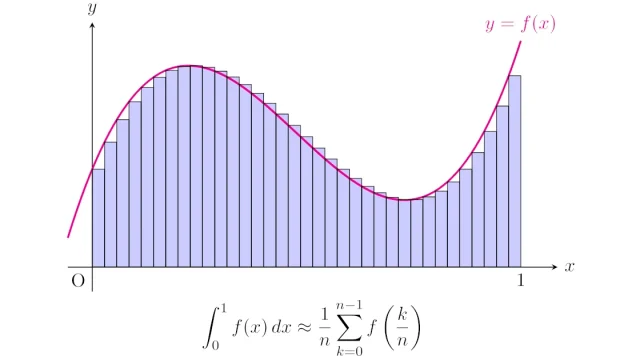 TikZ
TikZ 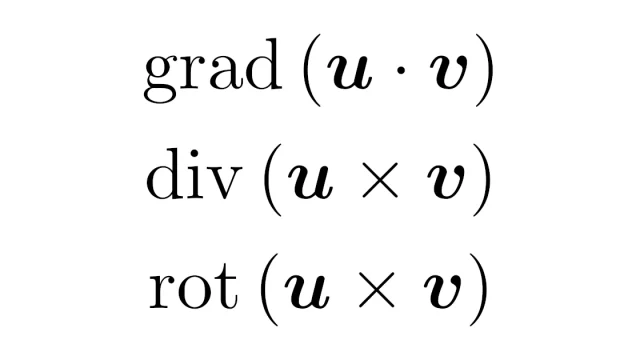 ベクトル解析
ベクトル解析 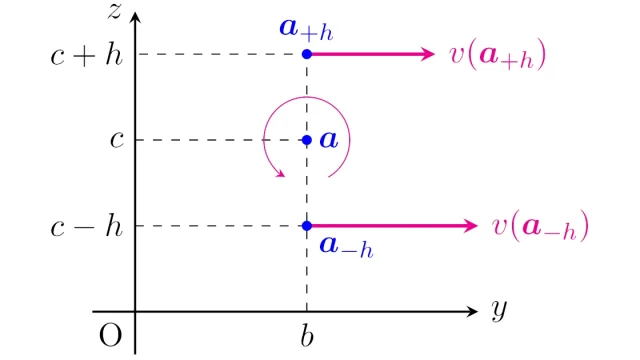 ベクトル解析
ベクトル解析