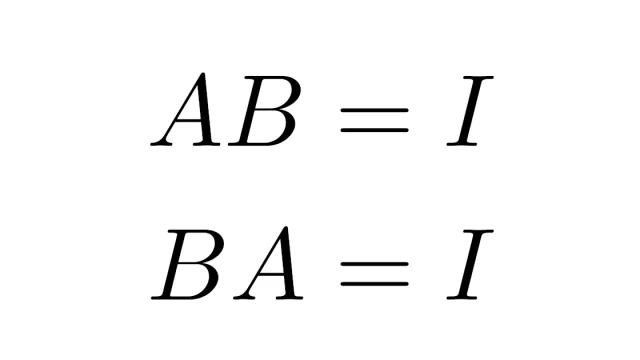 線形代数学の基本
線形代数学の基本 行列の正則条件を簡単に!AB=IまたはBA=Iであれば正則
正方行列Aが正則(逆行列をもつ)とは,AB=BA=Iとなる行列Bが存在することと定義されます.ところが,実はAB=IまたはBA=Iのどちらかが成り立ちさえすれば,自動的にAB=BA=Iが満たされAが正則となります.
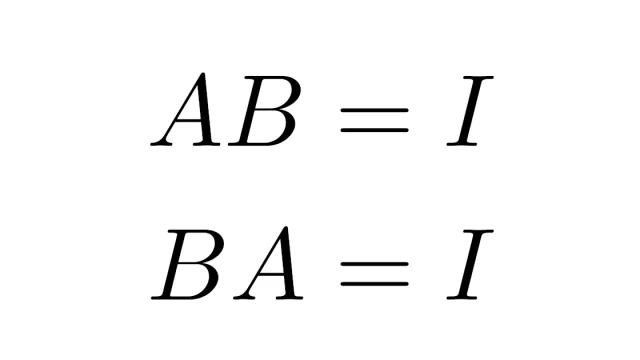 線形代数学の基本
線形代数学の基本 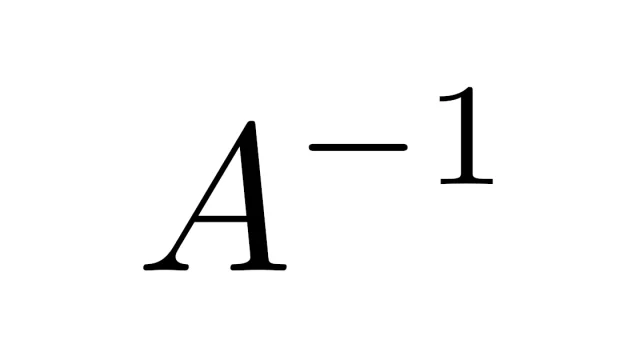 線形代数学の基本
線形代数学の基本  書評
書評  書評
書評  書評
書評  統計学
統計学  京都大学|大学院入試
京都大学|大学院入試  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本  微分方程式
微分方程式