 微分積分学
微分積分学 交項級数の定義と性質|正負の項が交互に並ぶ級数の収束性
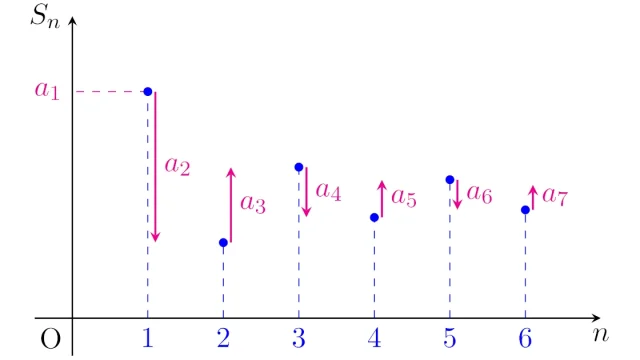
級数1-(1/3)+(1/5)-(1/7)+(1/9)-……のように,正の項と負の項が交互に足されており,一定の条件を満たす級数を「交項級数」といい,交項級数は必ず収束することが知られています.この記事では,交項級数が収束することを証明します.
 微分積分学
微分積分学 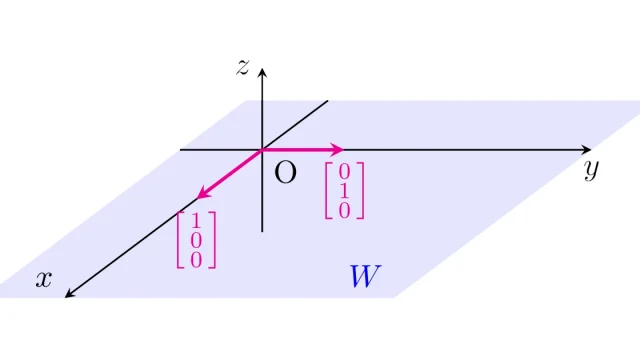 線形空間の基本
線形空間の基本 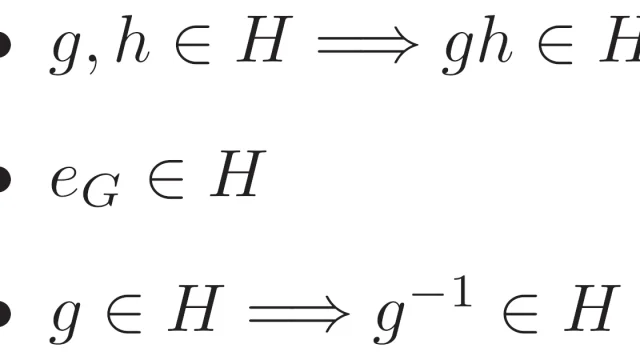 群論の基本
群論の基本 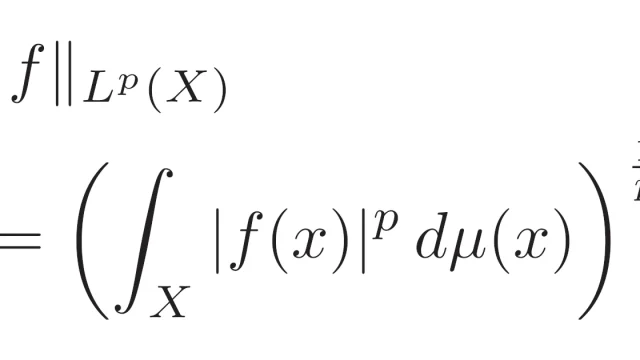 ルベーグ空間
ルベーグ空間  京都大学|大学院入試
京都大学|大学院入試 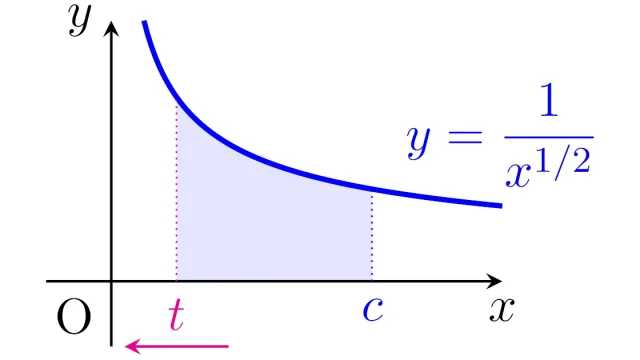 微分積分学
微分積分学  神戸大学|3年次編入試
神戸大学|3年次編入試 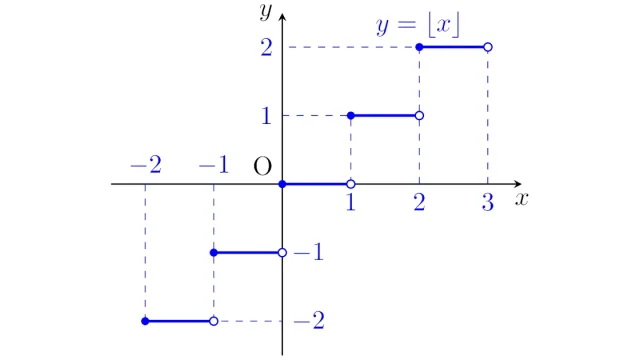 その他
その他 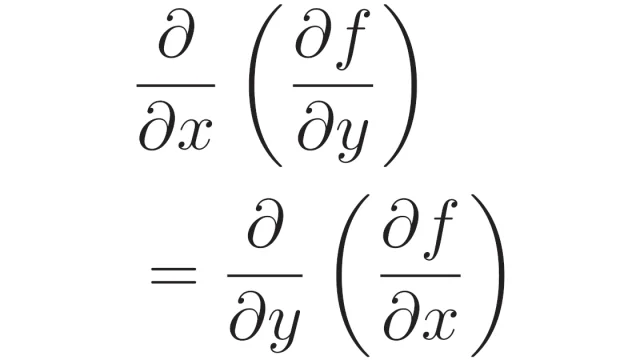 微分積分学
微分積分学 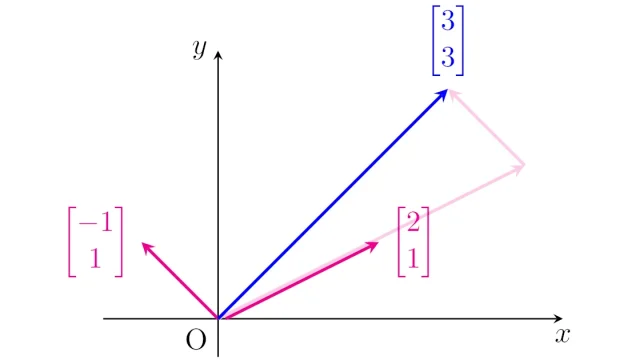 線形空間の基本
線形空間の基本