のちの記事で説明するように，ルベーグ積分はルベーグ可測関数に対して定義されます．
そのため，ルベーグ積分を学び進めるにあたって，ルベーグ可測関数の性質を整理しておくことは大切です．
この記事では，
- 可測関数たちの線形結合・積・商
- 可測関数の正成分・負成分・絶対値
を順に説明します．
この記事の内容は理論上重要ですが，証明は技術的なものが多いので，可測関数であることの証明に慣れるつもりで読むのが良いかもしれません．
「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
ルベーグ積分の参考文献
以下はルベーグ積分に関するオススメの教科書です．
ルベグ積分入門
ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．
ルベーグ積分と関数解析
ルベーグ積分から更なるステップに進みたい人向けの教科書です．
線形結合・積・商
可測関数をもとにできる関数の多くは可測関数です．ここでは，２つの可測関数の線形結合・積・商で定まる関数が可測関数であることを示します．
線形結合の可測性
まずは可測関数の線形結合の可測性を示します．
可測集合$A$上の可測関数$f,g$と$k,\ell\in\R$に対して，関数$kf+\ell g$は可測関数である．
この命題から「可測関数$A$上の可測関数全部の集合は通常の関数の和と定数倍で線形空間となる」ことが分かりますね．
定数倍よってできる関数$kf$，和によってできる関数$f+g$がそれぞれ可測関数であることを示せばよい．
定数倍の可測性
可測集合$A$上の可測関数$f$と$k\in\R$に対して，関数$kf$は可測関数である．
任意の$\alpha\in\R$に対して，
\begin{align*}A’:=&\set{x\in A}{(kf)(x)>\alpha}
\\=&\set{x\in A}{k\cdot f(x)>\alpha}\end{align*}
である．
［１］$k>0$のとき
\begin{align*}A’=\set{x\in A}{f(x)>\frac{\alpha}{k}}\end{align*}
が成り立つ．$f$は可測関数だから$A’\in\mathcal{L}$である．
［２］$k=0$のとき
\begin{align*}A’=\set{x\in A}{0>\alpha}=\begin{cases}A&(\alpha<0)\\\emptyset&(\alpha\ge0)\end{cases}\end{align*}
が成り立つ．$A,\emptyset\in\mathcal{L}$だから$A’\in\mathcal{L}$である．
［３］$k<0$のとき
\begin{align*}A’=\set{x\in A}{f(x)<\frac{\alpha}{k}}\end{align*}
が成り立つ．$f$は可測関数だから$A’\in\mathcal{L}$である．
［１］〜［３］より，$kf$は可測関数である．
和の可測性
可測集合$A$上の可測関数$f,g$に対して，関数$f+g$は可測関数であることを示す．
\begin{align*}A’:=&\set{x\in A}{(f+g)(x)>\alpha}
\\=&\set{x\in A}{f(x)+g(x)>\alpha}
\\=&\bigcup_{r\in\Q}\set{x\in A}{f(x)>r>-g(x)+\alpha}
\\=&\bigcup_{r\in\Q}\bra{\set{x\in A}{f(x)>r}\cap\set{x\in A}{g(x)>-r+\alpha}}\end{align*}
が成り立つ．$f,g$はともに可測関数だから
\begin{align*}\set{x\in A}{f(x)>r},\set{x\in A}{g(x)>-r+\alpha}\end{align*}
はともに可測集合であり，一般に可測集合の共通部分も可測集合だから
\begin{align*}\set{x\in A}{f(x)>r}\cap\set{x\in A}{g(x)>-r+\alpha}\end{align*}
も可測集合である．
さらに，$\Q$が可算集合であることと，$\mathcal{L}$が完全加法族であることを併せて$A’\in\mathcal{L}$である．
よって，$f+g$は可測関数である．
積の可測性
次に可測関数の積の可測性を示します．
可測集合$A$上の可測関数$f,g$に対して，関数$fg$は可測関数である．
２ステップで示す．
ステップ１（２乗$f^2$の可測性）
任意に$\alpha\in\R$をとる．$\alpha<0$なら$\set{x\in A}{f^2(x)>\alpha}=A\in\mathcal{L}$が成り立つ．
一方，$\alpha\ge0$なら
\begin{align*}A’:=&\set{x\in A}{f^2(x)>\alpha}
\\=&\set{x\in A}{f(x)<-\sqrt{\alpha}}\cup\set{x\in A}{f(x)>\sqrt{\alpha}}\end{align*}
が成り立つ．$f$は可測関数だから
\begin{align*}\set{x\in A}{f(x)<-\sqrt{\alpha}},\set{x\in A}{f(x)>\sqrt{\alpha}}\end{align*}
はともに可測集合であり，一般に可測集合の和集合も可測集合だから$A’\in\mathcal{L}$である．
よって，$f^2$は可測関数である．
ステップ２（積$fg$の可測性）
$f,g$の線形結合で表せる$f+g$, $f-g$はともに可測関数だから，ステップ１より$(f+g)^2$, $(f-g)^2$もともに可測関数である．
さきほど示したように，可測関数の線形結合も可測関数だから
\begin{align*}fg=\dfrac{1}{4}((f+g)^2-(f-g)^2)\end{align*}
も可測関数である．
商の可測性
補題を１つ示し，可測関数の商の可測性を示します．
２ステップで示す．
ステップ１（関数${1/f}$の可測性）
任意に$\alpha\in\R$をとる．
［１］$\alpha>0$のとき
\begin{align*}A_1:=&\set{x\in A}{\frac{1}{f(x)}>\alpha}
\\=&\set{x\in A}{\frac{1}{f(x)}>\alpha\ \text{and}\ f(x)>0}
\\=&\set{x\in A}{f(x)<\frac{1}{\alpha}}\cap\set{x\in A}{f(x)>0}\end{align*}
が成り立つ．$f$は可測関数だから
\begin{align*}\set{x\in A}{f(x)<\frac{1}{\alpha}},\set{x\in A}{f(x)>0}\end{align*}
はともに可測集合であり，一般に可測集合の共通部分も可測集合だから$A_1\in\mathcal{L}$である．
［２］$\alpha=0$のとき
\begin{align*}A_2:=\set{x\in A}{\frac{1}{f(x)}>\alpha}=\set{x\in A}{f(x)>0}\end{align*}
が成り立つ．$f$は可測関数だから$A_2\in\mathcal{L}$である．
［３］$\alpha<0$のとき
\begin{align*}A_3:=&\set{x\in A}{\frac{1}{f(x)}>\alpha}
\\=&\set{x\in A}{f(x)\ge0\ \text{or}\ \bra{\frac{1}{f(x)}>\alpha\ \text{and}\ f(x)<0}}
\\=&\set{x\in A}{f(x)\ge0}\cup\set{x\in A}{f(x)<\frac{1}{\alpha}}\end{align*}
が成り立つ．$f$は可測関数だから
\begin{align*}\set{x\in A}{f(x)\ge0},\set{x\in A}{f(x)<\frac{1}{\alpha}}\end{align*}
はともに可測集合であり，一般に可測集合の和集合も可測集合だから$A_3\in\mathcal{L}$である．
［１］〜［３］より，$\dfrac{1}{f}$は可測関数である．
ステップ２（$g/f$の可測性）
$g$は可測関数だから，補題より$\dfrac{1}{g}$も可測関数である．
もとより$f$は可測関数だから，$f$, $\dfrac{1}{g}$の積で表せる$\dfrac{f}{g}=f\cdot\dfrac{1}{g}$も可測関数である．
可測関数の正成分・負成分
関数の正成分・負成分はのちにルベーグ積分を定義する際に必要となるので，ここで定義して可測性も示しておきましょう．
正成分と負成分の定義
まずは関数の正成分と負成分を定義します．
$A\subset\R$とする．関数$f:A\to\R$に対して，
\begin{align*}f_+(x)=\max\{f(x),0\},\quad
f_-(x)=\max\{-f(x),0\}\end{align*}
で定まる関数$f_+,f_-:A\to\R$をそれぞれ$f$の正成分，負成分という．
$a,b\in\R$に対して$\max{a,b}$は$a,b$の小さくない方のことですね．
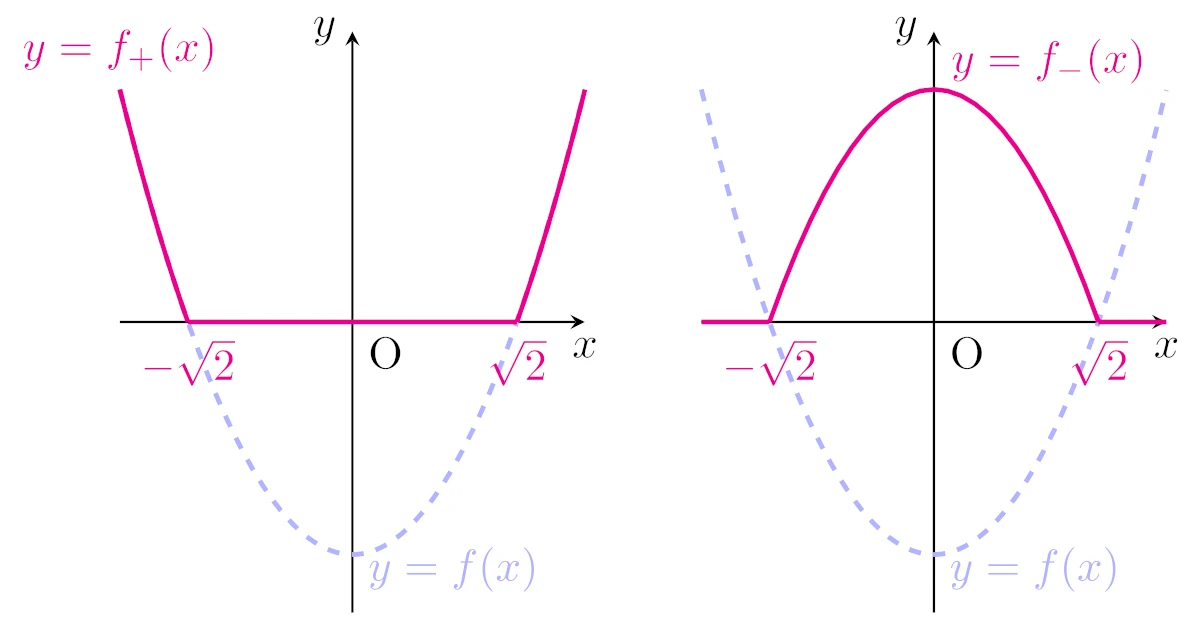
例えば，$f:\R\to\R;x\mapsto x^2-2$に対しては
\begin{align*}f_+(x)=&\max\{x^2-2,0\}
\\=&\begin{cases}x^2-2&(x<-\sqrt{2},\sqrt{2}<x)\\0&(-\sqrt{2}\le x\le\sqrt{2}),\end{cases}
\\f_-(x)=&\max\{-(x^2-2),0\}
\\=&\begin{cases}-x^2+2&(-\sqrt{2}<x<\sqrt{2})\\0&(x\le-\sqrt{2},\sqrt{2}\le x)\end{cases}\end{align*}
となりますね．
ざっくり言えば，関数の負の部分を全て０にしたものが正成分で，関数の正の部分を全て０にして$-1$をかけたものが負成分ですね．
また，一般に$t\in\R$に対して$\max\{t,0\}\ge0$なので，正成分$f_+$と負成分$f_-$は定義より非負値関数ですね．
正成分・負成分の可測性
可測関数の正成分・負成分の可測性を示します．
可測集合$A$上の可測関数$f$に対して，正成分$f_+$と負成分$f_-$は可測関数である．
任意に$\alpha\in\R$をとる．
［１］$\alpha<0$のとき，
\begin{align*}&\set{x\in A}{f_+(x)>\alpha}=A\in\mathcal{L},
\\&\set{x\in A}{f_-(x)>\alpha}=A\in\mathcal{L}\end{align*}
が成り立つ．
［２］$\alpha\ge0$のとき，
\begin{align*}&\set{x\in A}{f_+(x)>\alpha}=\set{x\in A}{f(x)>\alpha},
\\&\set{x\in A}{f_-(x)>\alpha}=\set{x\in A}{f(x)<-\alpha}\end{align*}
が成り立つ．$f$は可測関数だからこれらは可測集合である．
［１］［２］より，$f_+,f_-$はともに可測関数である．
絶対値の可測性
いまの命題より，可測関数の絶対値も可測であることが従います．
可測集合$A$上の可測関数$f$に対して，$|f|$は可測関数である．
いま示した命題より$f_{+},f_{-}$である．
よって，これらの和で表せる$|f|=f_{+}+f_{-}$も可測関数である．
連続関数の可測性
最後に連続関数の可測性を示します．
$f$を$A$上の連続関数とする．任意の$\alpha\in\R$に対して，
\begin{align*}\set{x\in\R}{f(x)\ge\alpha}=f^{-1}([\alpha,\infty])\end{align*}
である．ただし，ルベーグ積分で扱う関数の終集合は拡大実数$\overline{\R}=\R\cup\{\infty,-\infty\}$であることに注意．
ここで，拡大実数において
- $p\in(-\infty,\alpha)$なら$(p-1,\frac{\alpha+p}{2})$は$p$の開近傍で$(p-1,\frac{\alpha+p}{2})\subset[-\infty,\alpha)$
- $p=-\infty$なら$[-\infty,\alpha)$自体が$p$の開近傍
なので，$[-\infty,\alpha)$は開集合となる．よって，$[\alpha,\infty]=[-\infty,\alpha)^c$は閉集合である．
位相空間における連続関数の定義から，閉集合の引き戻しは閉集合だから$f^{-1}([\alpha,\infty])$は閉集合である．一般に閉集合は可測集合だから$f^{-1}([\alpha,\infty])$は可測集合である．
コメント