ルベーグ積分（測度論）を扱う分野では，$p$乗可積分に関する不等式であるヘルダー（Hölder）の不等式がよく用いられます．
ヘルダーの不等式を用いると可測関数$f,g$の積$fg$が可積分であることを証明できるなど，ルベーグ積分において最も基本的な不等式のひとつです．
この記事では，
- $p$乗ルベーグ可積分関数
- ヘルダーの不等式
- ヘルダーの不等式の応用
を順に説明します．
「ルベーグ空間$L^p$の基本」の一連の記事
ルベーグ空間（$L^p$空間）の参考文献
以下は関数解析に関するオススメの教科書です．
関数解析
ロングセラーの入門書です．基礎から具体例に触れつつ解説されており，初学者にも理解しやすいテキストです．
ルベーグ積分と関数解析
ルベーグ積分から更なるステップに進みたい人向けの教科書です．
$p$乗ルベーグ可積分関数
まずは$p$乗可積分関数を定義しましょう．
可測集合$A\subset\R$上の可測関数$f$と$p\ge1$に対して，
\begin{align*}\int_{A}|f(x)|^p\,dx<\infty\quad\dots(*)\end{align*}
が成り立つとき，$f$は$A$における$p$乗可積分であるという．
条件$(*)$は$|f|^p$がルベーグ可積分であると言っても同じことですね．
例えば，$f:\R\to\R;x\mapsto\dfrac{1}{\sqrt{1+x^2}}$は可測集合$\R$上の可測関数であり，
\begin{align*}\int_{\R}|f(x)|^2\,dx
&=\int_{\R}\frac{1}{1+x^2}\,dx
=\brc{\tan^{-1}{x}}_{-\infty}^{\infty}
\\&=\frac{\pi}{2}-\bra{-\frac{\pi}{2}}
=\pi\end{align*}
となるので，$f$は$\R$における２乗可積分関数ですね．
ヘルダーの不等式
補題をひとつ示してから，ヘルダーの不等式を証明します．
補題
$p,q>1$は$\frac{1}{p}+\frac{1}{q}=1$を満たすとする．このとき，任意の$a,b\ge0$に対して，不等式
\begin{align*}ab\le \frac{a^p}{p}+\frac{b^q}{q}\end{align*}
が成り立つ．
$a=0$または$b=0$のときは両辺とも０なので等号で成り立つから，以下$a\neq0$かつ$b\neq0$とする．
対数関数$\log$は上に凸だから，$\frac{1}{p}+\frac{1}{q}=1$に注意してイェンセンの不等式を用いると
\begin{align*}\log{\bra{\frac{a^p}{p}+\frac{b^q}{q}}}
&\le\frac{1}{p}\log{a^p}+\frac{1}{q}\log{b^q}
\\&=\log{a}+\log{b}=\log{ab}\end{align*}
が成り立つ．
よって，対数関数が単調増加であることと併せて$\frac{a^p}{p}+\frac{b^q}{q}\ge ab$を得る．
ヘルダーの不等式と証明
次の不等式をヘルダーの不等式といいます．
［ヘルダーの不等式］$A\subset\R$を可測集合とし，$p,q>1$は$\frac{1}{p}+\frac{1}{q}=1$を満たすとする．このとき，$A$上の可測関数$f,g$に対して，不等式
\begin{align*}\int_{A}|f(x)g(x)|\,dx\le\bra{\int_{A}|f(x)|^p\,dx}^{1/p}\bra{\int_{A}|g(x)|^q\,dx}^{1/q}\end{align*}
が成り立つ．
ヘルダーの不等式から$p$乗可積分関数$f$と$q$乗可積分関数$g$の積$fg$は，１乗可積分関数（普通の可積分関数）であることが従いますね．
なお，$\frac{1}{p}+\frac{1}{q}=1$を満たす$p,q\in[1,\infty]$をヘルダー共役（Hölder conjugate）といいます．よく用いられるので知っておいてください．
$p=1$のときは$q=\infty$とみなし，$q=1$のときは$p=\infty$とみなします．
$F:=\bra{\int_{A}|f(x)|^p\,dx}^{1/p}$, $G:=\bra{\int_{A}|g(x)|^q\,dx}^{1/q}$とおく．
もし$F=0$または$G=0$なら，ほとんど至る所で$f=0$または$g=0$なので両辺とも$0$となって不等式が等号で成り立つから，$F\neq0$かつ$G\neq0$で考えれば良い．
さらに，もし$F=\infty$または$G=\infty$なら，右辺が$\infty$となって不等式が成り立つから，さらに$F\neq\infty$かつ$G\neq\infty$で考えれば良い．
任意の$x\in A$に対して，先ほど示した補題を$a=\frac{|f(x)|}{F}$, $b=\frac{|g(x)|}{G}$として適用すると，
\begin{align*}\frac{|f(x)g(x)|}{FG}
=\frac{|f(x)|}{F}\cdot\frac{|g(x)|}{G}
\le\frac{|f(x)|^p}{pF^p}+\frac{|g(x)|^q}{qG^q}\end{align*}
が成り立つ．よって，$F^p=\int_{A}|f(x)|^p\,dx$, $G^q=\int_{A}|g(x)|^q\,dx$に注意して，$\frac{1}{p}+\frac{1}{q}=1$を用いると
\begin{align*}&\int_{A}|f(x)g(x)|\,dx
\le FG\int_{A}\bra{\frac{|f(x)|^p}{pF^p}+\frac{|g(x)|^q}{qG^q}}\,dx
\\&=FG\bra{\frac{1}{pF^p}\int_{A}|f(x)|^p\,dx+\frac{1}{qG^q}\int_{A}|g(x)|^q\,dx}
\\&=FG\bra{\frac{1}{p}+\frac{1}{q}}
=FG\end{align*}
を得る．
コーシー-シュワルツの不等式
いま示したヘルダーの不等式で$p=q=2$としたときの不等式をコーシー（cauchy）-シュワルツ（Schwartz）の不等式といいます：
［コーシー-シュワルツの不等式］$A\subset\R$を可測集合とする．このとき，$A$上の２乗可積分関数$f$, $g$に対して，不等式
\begin{align*}\bra{\int_{A}|f(x)g(x)|\,dx}\le\bra{\int_{A}|f(x)|^2\,dx}^{1/2}\bra{\int_{A}|g(x)|^2\,dx}^{1/2}\end{align*}
が成り立つ．
コーシー-シュワルツの不等式から２乗可積分関数$f,g$の積$fg$は，１乗可積分関数（普通の可積分関数）であることが従いますね．
ヘルダーの不等式の応用（双対性）
ヘルダーの不等式を用いると，次の等式が導かれます．
$A\subset\R$を可測集合とし，$p,q>1$は$\frac{1}{p}+\frac{1}{q}=1$を満たすとする．このとき，$A$上の可測関数$f$に対して，等式
\begin{align*}\bra{\int_{A}|f(x)|^p\,dx}^{1/p}=\sup\set{\int_{A}|f(x)g(x)|\,dx}{\bra{\int_{A}|g(x)|^q\,dx}^{1/q}=1}\end{align*}
が成り立つ．
つまり，可測関数$g$を$\int_{A}|g(x)|^q\,dx=1$を満たしながら動かすときの$\int_{A}|f(x)g(x)|\,dx$の上限が$\bra{\int_{A}|f(x)|^p\,dx}^{1/p}$に一致するわけですね．
もし$\int_{A}|f(x)|^p\,dx=0$なら，ほとんど至る所で$f=0$なので両辺とも$0$となって成り立つから，$\int_{A}|f(x)|^p\,dx\neq0$で考えれば良い．
$\bra{\int_{A}|g(x)|^q\,dx}^{1/q}=1$を満たす任意の可測関数$g$に対して，ヘルダーの不等式より
\begin{align*}\int_{A}|f(x)g(x)|\,dx
&\le\bra{\int_{A}|f(x)|^p\,dx}^{1/p}\bra{\int_{A}|g(x)|^q\,dx}^{1/q}
\\&=\bra{\int_{A}|f(x)|^p\,dx}^{1/p}\end{align*}
が成り立つ．よって，
\begin{align*}\bra{\int_{A}|f(x)|^p\,dx}^{1/p}\ge\sup\set{\int_{A}|fg(x)|\,dx}{\bra{\int_{A}|g(x)|^q\,dx}^{1/q}=1}\end{align*}
が成り立つ．
一方，$g(x):=|f(x)|^{p-1}\bra{\int_{A}|f(x)|^p\,dx}^{-1/q}$とおくと，
\begin{align*}&\int_{A}|f(x)g(x)|\,dx
=\bra{\int_{A}|f(x)|^p\,dx}^{-1/q}\int_{A}|f(x)|^p\,dx
\\&=\bra{\int_{A}|f(x)|^p\,dx}^{1-(1/q)}
=\bra{\int_{A}|f(x)|^p\,dx}^{1/p}\end{align*}
となるから，
\begin{align*}\bra{\int_{A}|f(x)|^p\,dx}^{1/p}\le\sup\set{\int_{A}|f(x)g(x)|\,dx}{\bra{\int_{A}|g(x)|^q\,dx}^{1/q}=1}\end{align*}
が成り立つ．
この等式を用いて$\bra{\int_{A}|f(x)|^p\,dx}^{1/p}$を考えることを双対性議論（duality argument）などと呼ぶことがあります．
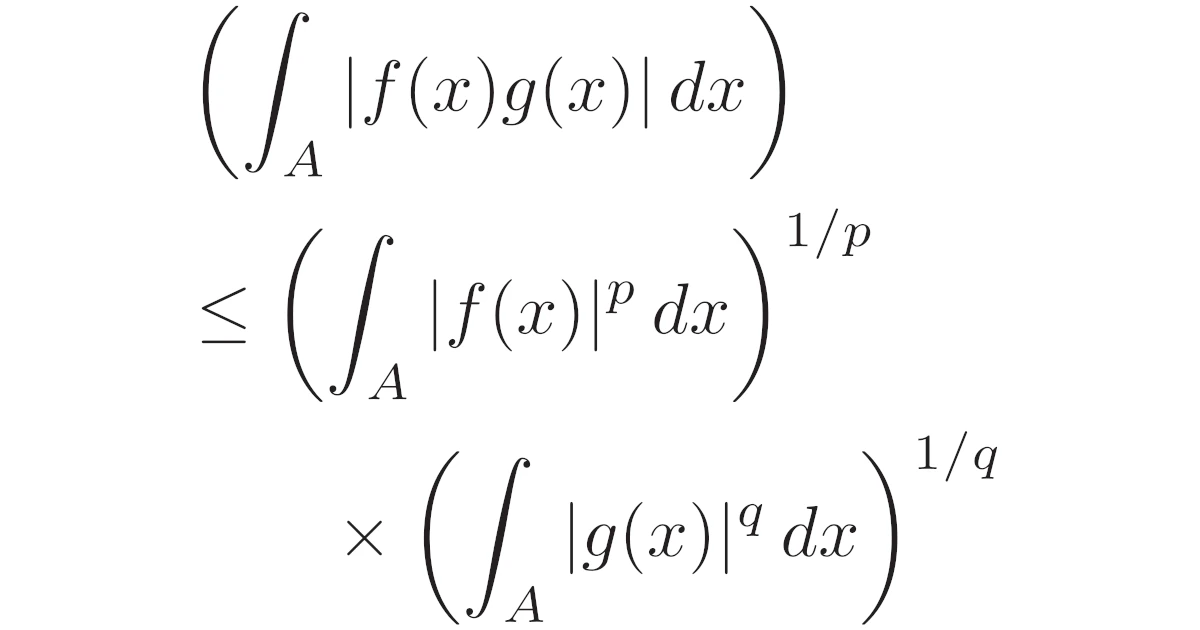
コメント