本質的有界な関数のルベーグ空間L^∞｜ノルム空間として定義

例えば，関数$f:\R\to\R$を

$\begin{align*}f(x)=\begin{cases}\cos{x}&(x\neq0),\\2&(x=0)\end{cases}\end{align*}$

で定めると，この関数は$x=0$での値が飛び跳ねていますが，本質的には$\cos{x}$なので$f$の本質的上限は

$\begin{align*}\esssup_{n\in\R}f(x)=1\end{align*}$

と表すのでした．

実は（適切な同一視のもとで）可測集合上の本質的有界な可測関数全部の集合$L^{\infty}$はバナッハ空間（完備なノルム空間）となります．この空間$L^{\infty}$をルベーグ空間と言います．

この記事ではノルム空間となることまで証明し，完備性はのちの記事（準備中）で証明します．

この記事では

可測関数の同一視
ルベーグ空間$L^\infty$の定義
補足（同値類の空間が線形空間となることの証明）

を順に解説します．

「ルベーグ空間$L^p$の基本」の一連の記事

ルベーグ空間（$L^p$空間）の参考文献
可測関数の同一視
1. ノルム空間の復習
2. 可測関数の同一視
ルベーグ空間$L^{\infty}$の定義
1. 本質的有界な関数の同値類
2. ルベーグ空間$L^{\infty}$の定義
補足（同値類の空間が線形空間となることの証明）

ルベーグ空間（$L^p$空間）の参考文献

以下は関数解析に関するオススメの教科書です．

関数解析

ロングセラーの入門書です．基礎から具体例に触れつつ解説されており，初学者にも理解しやすいテキストです．

ルベーグ積分と関数解析

ルベーグ積分から更なるステップに進みたい人向けの教科書です．

可測関数の同一視

ルベーグ空間$L^{\infty}$をきちんと定義するには同値関係（商集合）を考える必要があります．

まずはノルム空間の定義から同値関係（商集合）が必要となる理由を考えましょう．

ノルム空間の復習

ルベーグ空間$L^p$をノルム空間として定義したいので，まずはノルム空間を復習しておきましょう．

体$\R$上の線形空間$V$に対して，関数$\|\cdot\|:V\to\R$が

［非退化性］$\m{x}\in V$に対し$\|\m{x}\|=0 \iff \m{x}=\m{0}$
［斉次性］任意の$\alpha\in\R$, $x\in V$に対し$\|\alpha \m{x}\|=|\alpha|\|\m{x}\|$
［劣加法性］任意の$\m{x},\m{y},\m{z}\in V$に対し$\|\m{x}-\m{z}\|\le\|\m{x}-\m{y}\|+\|\m{y}-\m{z}\|$

の全てを同時に満たすとき，$\|\cdot\|$を$V$のノルム（norm）といい，組$(V,\|\cdot\|)$をノルム空間（norm space）という．

以下では$X\subset\R$上の可測関数全部の集合を$L(X)$と表しましょう．

$L(X)$は通常の関数の和とスカラー倍により可測関数全部の集合は線形空間となるのでした．$\R$上で恒等的に値０をとる関数が零ベクトルとなりますね．

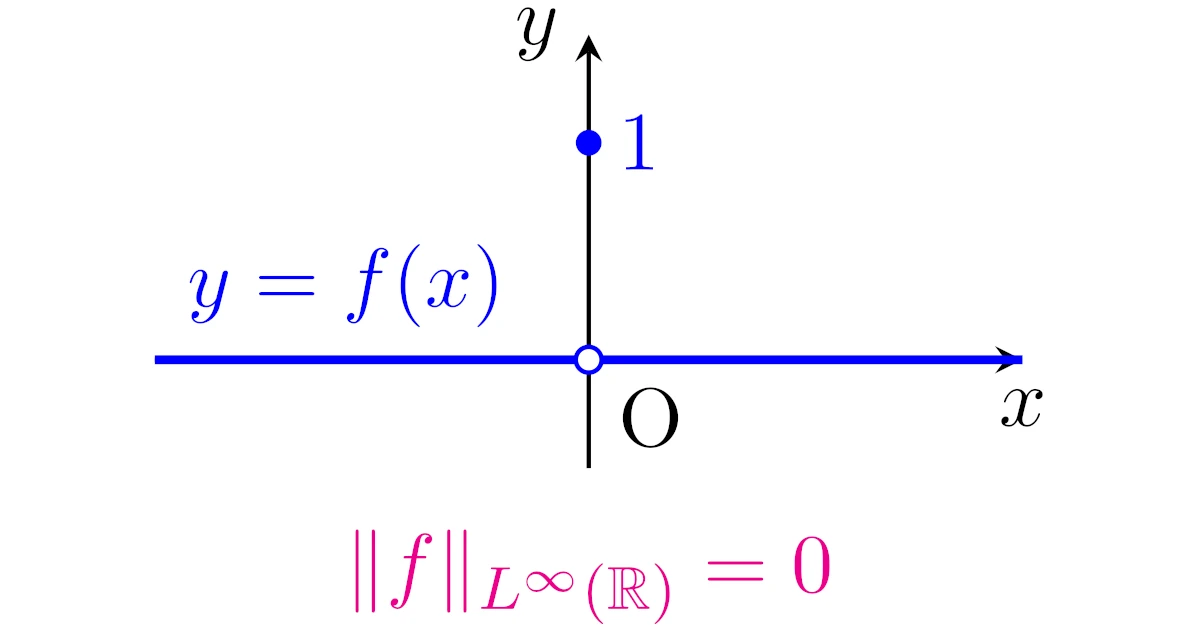
さて，$L(X)$の本質的有界な関数全部の線形部分空間にノルム$\|f\|_{\infty}:=\esssup\limits_{n\in\R}|f(x)|$を考えようとすると，例えば

$\begin{align*}f(x)=\begin{cases}0&(x\neq0)\\1&(x=0)\end{cases}\end{align*}$

と定まる関数$f:\R\to\R$は本質的に有界で$\|f\|_{\infty}=0$を満たします．

ほとんど至る所で等しい（零集合上のみで異なる）２つの可測関数の本質的上限は等しいので，この関数$f$以外にも$\|f\|_{\infty}=0$となる可測関数$f$はたくさんありますね．

ところが，$\|\cdot\|_{\infty}$がノルムなら非退化性から$\|f\|_{\infty}=0$となる関数は零ベクトルのみでないといけませんから，単純には$\|\cdot\|_{\infty}$をノルムと定義することができません．

可測関数の同一視

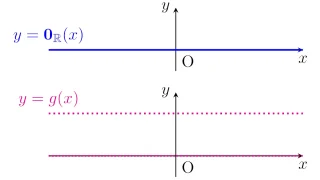
そこでほとんど至る所で等しい２つの関数たちを同一視する同値関係を考えましょう．

可測集合$X\subset\R^d$上の可測関数全部の集合に，関係$\sim$を

$\begin{align*}f\sim g\stackrel{\mathrm{def.}}{\iff}m(\set{x\in X}{f(x)\neq g(x)})=0\end{align*}$

を定めると，関係$\sim$は同値関係となる．ただし，$m$はルベーグ測度である．

つまり，ほとんど至る所で等しい関数たちをまとめてグループ分けできるということですね．

この補題の証明は以下の記事を参照してください．

「ほとんど至る所」の定義・具体例・応用｜測度空間の零集合

ルベーグ積分では零集合上でのみ例外であることを「ほとんど至る所で」と言います．この記事では「ほとんど至る所で」の定義と具体例を解説したのち，ほとんど至る所で等しい関数の同一視についても解説します．

ルベーグ空間$L^{\infty}$の定義

定義域が$X\subset\R$の本質的有界な関数$f$は$\esssup\limits_{x\in X}|f(x)|<\infty$を満たすことに注意してください．

以下では，ほとんど至る所で等しい関数たちを同一視してできる商集合を$\tilde{L}(X)$と表しましょう．

$L(X)$が線形空間であることから$\tilde{L}(X)$も線形空間となります．このことはこの記事の最後で証明しています．

本質的有界な関数の同値類

一般にほとんど至る所で等しい関数を同一視する同値関係$\sim$に関して，同じ同値類に属する２つの関数は等しい本質的上限をもちます．

可測集合$X\subset\R^d$を考える．$F\in\tilde{L}(X)$のある代表元$f$が本質的有界なら，任意の$g\in F$は本質的有界であり，

$\begin{align*}\esssup\limits_{x\in X}|f(x)|=\esssup\limits_{x\in X}|g(x)|\end{align*}$

が成り立つ．

$f,g\in F$だから，$f$と$g$はほとんど至る所で等しいので，$|f|$と$|g|$もほとんど至る所で等しい．

$L:=\esssup\limits_{x\in X}|f(x)|$とすると，

$\begin{align*}&\set{x\in X}{|g(x)|>L} \\&\subset\set{x\in X}{|f(x)|>L,f(x)=g(x)}\cup\set{x\in X}{f(x)\neq g(x)} \\&\subset\set{x\in X}{|f(x)|>L}\cup\set{x\in X}{f(x)\neq g(x)}\end{align*}$

なので，$f$が本質的有界ならルベーグ測度$m$の単調性と劣加法性より

$\begin{align*}&m(\set{x\in X}{|g(x)|>L}) \\&\le m(\set{x\in X}{|f(x)|>L})+m(\set{x\in X}{f(x)\neq g(x)}) \\&=0+0=0\end{align*}$

が成り立ち，$g$が本質的有界で$\esssup\limits_{x\in X}|g(x)|\le L$と分かる．

一方，$L’=\esssup\limits_{x\in X}|g(x)|$とすれば，今の議論と同様にして$L\le L’$が分かるので$L=L’$が従う．

いまの補題から本質的有界な可測関数$f$が属する同値類$F$に対して$\|F\|_{\infty}:=\|f\|_{\infty}$と定義できます（well-definedです）ね．

ルベーグ空間$L^{\infty}$の定義

$\tilde{L}(X)$の同値類も通常の関数のように扱っても問題がないことが多く，実際ほとんどの場合で通常の関数のように扱います．

$\tilde{L}(X)$の同値類を表す文字も，同値類を通常の関数のように$f,g$などを使います．

$\tilde{L}(X)$の本質的有界な関数（厳密には同値類）全部の集合$L^{\infty}(X)$は，$\tilde{L}(X)$の線形部分空間となります．

可測集合$X\subset\R^d$を考える．

$\begin{align*}\|f\|_{\infty}:=\esssup_{x\in X}|f(x)|<\infty\end{align*}$

をみたす$f\in\tilde{L}(X)$全部の集合$L^{\infty}(X)$は，$\tilde{L}(X)$の線形部分空間となる．さらに，$\|\cdot\|_{\infty}$は$L^{\infty}(X)$上のノルムとなる．

［部分空間となること］任意に$f,g\in L^\infty(X)$と$k\in\R$をとる．本質的上限$\esssup$の劣加法性と絶対値の劣加法性より

$\begin{align*}\esssup_{x\in X}|f(x)+g(x)|\le&\esssup_{x\in X}(|f(x)|+|g(x)|) \\\le&\esssup_{x\in X}|f(x)|+\esssup_{x\in X}|g(x)|\end{align*}$

なので$f+g\in L^{\infty}(X)$である．また，絶対値の斉次性と$\sup$が定数倍を保つことから

$\begin{align*}\esssup_{x\in X}|kf(x)|=\esssup_{x\in X}|k||f(x)|=|k|\esssup_{x\in X}|f(x)|\end{align*}$

なので$kf\in L^{\infty}(X)$である．よって，$L^{\infty}(X)$は$\tilde{L}(X)$の部分空間となる．

［ノルム空間となること］恒等的に値０をとる関数を$0_{\R}$とすると$\|0_{\R}\|_{\infty}=0$である．

逆に$f\in\tilde{L}(X)$が$\|f\|_{\infty}=0$を満たせば$|f|$はほとんど至る所で値０をとるから$f$はほとんど至る所で$0_{\R}$に等しい．

部分空間であることの証明で斉次性・劣加法性が示されている．

この補題の空間$L^{\infty}(X)$をルベーグ空間といいます．

可測集合$X\subset\R^d$上の可測関数全部の集合$\tilde{L}(X)$の，本質的有界な関数全部の線形部分空間

$\begin{align*}\set{f\in\tilde{L}(X)}{\|f\|_\infty:=\esssup_{x\in X}|f(x)|<\infty}\end{align*}$

のノルム$\|\cdot\|_{\infty}$を備えたノルム空間をルベーグ空間（Lebesgue space）といい，$L^\infty(X)$と表す．

集合$X$上で$\esssup$を考えていることを強調して，ノルム$\|\cdot\|_{\infty}$を$\|\cdot\|_{L^{\infty}(X)}$と表すこともよくあります．

絶対値の$p$乗が可積分な可測関数の空間$L^p$もルベーグ空間と呼びます．

補足（同値類の空間が線形空間となることの証明）

最後に$X\subset\R$上の可測関数全部の集合$L(X)$をほとんど至る所で等しい関数たちを同一視してできる商集合$\tilde{L}(X)$が通常の和とスカラー倍によって線形空間となることを証明しておきましょう．

可測集合$X\subset\R^d$に対して，$\tilde{L}(X)$上の演算$+$と作用$\cdot$を

$F,G\in\tilde{L}(X)$に対して，代表元$f\in F$, $g\in G$をとり，通常の関数の和$f+g$が属する同値類を$F+G$
$F\in\tilde{L}(X)$, $k\in\R$に対して，代表元$f\in F$をとり，通常の関数のスカラー倍$kf$が属する同値類を$k\cdot F$

と定めることができ，$\tilde{L}(X)$はそれぞれを和・スカラー倍として線形空間となる．

$X$上で恒等的に値０をとる関数を$0_{X}$と表す．$0_{X}\in\tilde{L}(X)$だから$\tilde{L}(X)\neq\emptyset$である．

［演算と作用のwell-defined性］$F,G\in\tilde{L}(X)$と$k\in\R$を考える．

代表元$f_1,f_2\in F,g_1,g_2\in G$をとると，$f_1,f_2$はほとんど至る所で等しく，$g_1,g_2$もほとんど至る所で等しいから