ルベーグ積分はルベーグ可測関数に対して考えることができますが，ルベーグ可測関数に対してルベーグ積分を定義するには少々準備が必要です．
その準備として，単関数と呼ばれるタイプの関数に対するルベーグ積分を考えておきましょう．
この記事では
- 単関数の定義と具体例
- 単関数がルベーグ可測関数であるための必要十分条件
- ルベーグ可測単関数のルベーグ積分
を順に説明します．
「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
ルベーグ積分の参考文献
以下はルベーグ積分に関するオススメの教科書です．
ルベグ積分入門
ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．
ルベーグ積分と関数解析
ルベーグ積分から更なるステップに進みたい人向けの教科書です．
単関数の定義と具体例
$A\subset\R$とする．関数$f:A\to\R$が（$A$上の）単関数（simple function）であるとは，$f$が有限個の値のみをとることをいう．
いくつか具体例をみてみましょう．
具体例１（値１，２，３のみをとる関数）
関数$f:[0,3]\to\R$を
\begin{align*}f(x)=\begin{cases}2&(0\le x<\frac{3}{2})\\3&(\frac{3}{2}\le x<3)\\1&(3\le x\le5)\end{cases}\end{align*}
で定めると，$f$のとる値は１，２，３のみの有限個ですから単関数ですね．
具体例２（ディリクレ関数）
関数$f:\R\to\R$を
\begin{align*}f(x)=\begin{cases}1&(x\in\Q)\\0&(x\in\R\setminus\Q)\end{cases}\end{align*}
で定めると，$f$のとる値は０，１のみの有限個ですから単関数ですね．この関数はディリクレ関数（Dirichlet function）という名前がついています．
$\R$上で$\Q$も$\R\setminus\Q$も稠密ですから，このディリクレ関数$f$は極めて細かく０と１を行き交うグラフをもちますね．
単関数がルベーグ可測であるための必要十分条件
冒頭でも少し触れたように，ルベーグ積分は可測関数に対して定義されます．
そのため，単関数のルベーグ積分を考えるためには，単関数が可測関数であるための条件を知っておく必要があります．
可測集合$A$上の単関数$f$の値域が$\{\alpha_1,\dots,\alpha_n\}$であるとき，次は同値である．
- $f$は$A$上の可測関数
- 任意の$k\in\{1,2,\dots,n\}$に対して$\set{x\in A}{f(x)=\alpha_k}\in\mathcal{L}$
要するに，単関数がとる全ての値$\alpha_k$に対して，集合$\set{x\in A}{f(x)=\alpha_k}$が可測集合であることが必要十分条件なわけですね．
単関数$f$が可測関数であるとき，$f$を可測単関数と呼びます．
具体例１（値１，２，３のみをとる関数）
関数
\begin{align*}f:[0,3]\to\R;x\mapsto\begin{cases}2&(0\le x<\frac{3}{2})\\3&(\frac{3}{2}\le x<3)\\1&(3\le x\le5)\end{cases}\end{align*}
の値域は$\{1,2,3\}$です．
さらに，
\begin{align*}&\set{x\in[0,3]}{f(x)=1}=[2,3],
\\&\set{x\in[0,3]}{f(x)=2}=[0,\tfrac{3}{2}),
\\&\set{x\in[0,3]}{f(x)=3}=[\tfrac{3}{2},2)\end{align*}
であり，一般に区間は可測集合なので，これらはいずれも可測集合です．よって，この$f$は可測単関数ですね．
具体例２（ディリクレ関数）
ディリクレ関数
\begin{align*}f:\R\to\R;x\mapsto\begin{cases}1&(x\in\Q)\\0&(x\in\R\setminus\Q)\end{cases}\end{align*}
の値域は$\{0,1\}$です．
さらに，
\begin{align*}&\set{x\in\R}{f(x)=0}=\R\setminus\Q,
\\&\set{x\in\R}{f(x)=1}=\Q\end{align*}
であり，
- 一般に可算集合は可測集合だから$\Q$は可測集合
- $\R$は可測集合であり，一般に可測集合の差集合は可測集合だから$\R\setminus\Q$は可測集合
なので，ディリクレ関数$f$は可測単関数ですね．
単関数がルベーグ可測であるための必要十分条件の証明
（再掲）可測集合$A$上の単関数$f$の値域が$\{\alpha_1,\dots,\alpha_n\}$であるとき，次は同値である．
- $f$は$A$上の可測関数
- 任意の$k\in\{1,2,\dots,n\}$に対して$\set{x\in A}{f(x)=\alpha_k}\in\mathcal{L}$
$(1)\Ra(2)$の証明
任意の$k\in\{1,2,\dots,n\}$に対して，
\begin{align*}\set{x\in A}{f(x)=\alpha_k}
=\set{x\in A}{\alpha_k\le f(x)\le\alpha_k}\end{align*}
であり，前回の記事で示したようにこれは可測集合である．
$(2)\Ra(1)$の証明
$\alpha_1<\alpha_2<\dots<\alpha_n$としてよい．任意に$\alpha\in\R$をとる．
- $\alpha\le\alpha_1$のときは\begin{align*}\set{x\in A}{f(x)\ge\alpha}=A\in\mathcal{L}\end{align*}
- $\alpha_{k-1}<\alpha\le\alpha_{k}$ ($k=1,2,\dots,n$)のときは\begin{align*}\set{x\in A}{f(x)\ge\alpha}=\set{x\in A}{f(x)\ge\alpha_{k}}\in\mathcal{L}\end{align*}
- $\alpha_n<\alpha$のときは\begin{align*}\set{x\in A}{f(x)\ge\alpha}=\emptyset\in\mathcal{L}\end{align*}
である．よって，任意の$\alpha\in\R$に対して$\set{x\in A}{f(x)\ge\alpha}$は可測集合なので，可測関数の定義より$f$は$A$上の可測関数である．
ルベーグ可測単関数のルベーグ積分
準備ができたので，可測単関数のルベーグ積分を定義しましょう．
単関数のルベーグ積分の考え方と定義
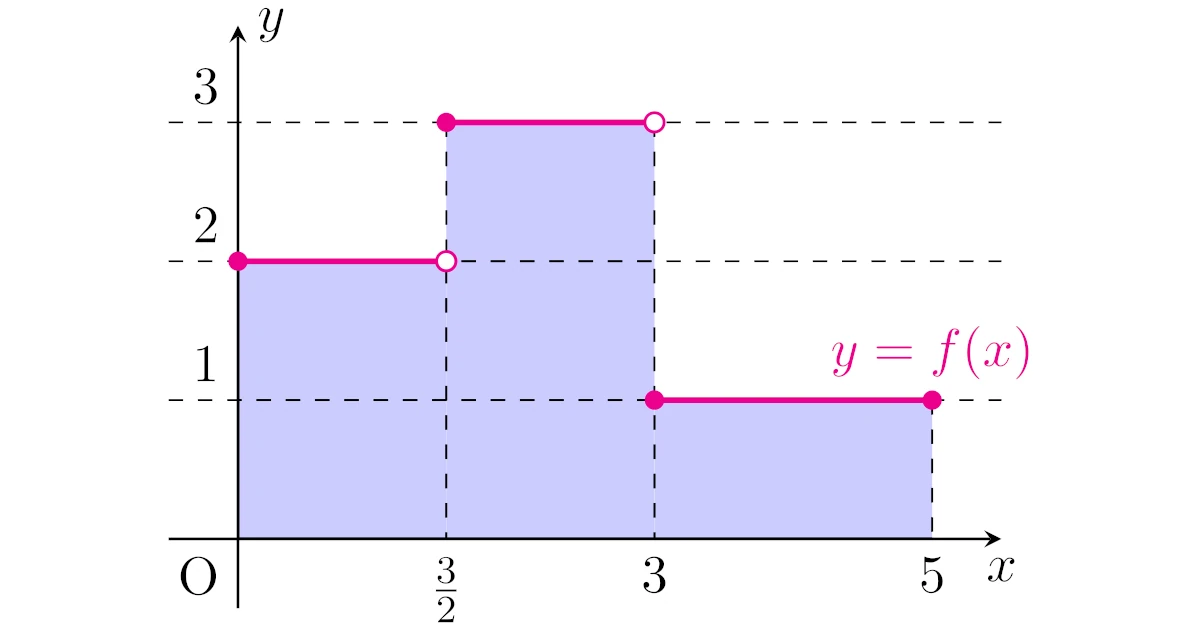
リーマン積分と同様に，ルベーグ積分も「$x$軸とグラフの間の部分の面積を表すもの」となるように定義したいので，先ほどから見ている具体例１の関数
\begin{align*}f:[0,3]\to\R;x\mapsto\begin{cases}2&(0\le x<\frac{3}{2})\\3&(\frac{3}{2}\le x<3)\\1&(3\le x\le5)\end{cases}\end{align*}
の積分は下図の長方形の面積の和になるように定めたいところです．
つまり，積分が
- $1\times m(\set{x\in[0,3]}{f(x)=1})$
- $2\times m(\set{x\in[0,3]}{f(x)=2})$
- $3\times m(\set{x\in[0,3]}{f(x)=3})$
の和となっていて欲しいですね．一般に可測単関数のルベーグ積分を次のように定義します．
可測集合$A$上の可測単関数$f$の値域が$\{\alpha_1,\dots,\alpha_n\}$であるとき，和
\begin{align*}\sum_{k=1}^{n}\alpha_k\times m(\set{x\in A}{f(x)=\alpha_k})\end{align*}
を可測単関数$f$の$A$上のルベーグ積分をといい，$\dint_{A}f(x)\,dm(x)$や単に$\dint_{A}f(x)\,dx$となどと表す．
この単関数のルベーグ積分の定義は，一般の可測関数のルベーグ積分の定義に矛盾しません．このことはのちの記事で証明しています．
可測単関数$f$がとる全ての値$\alpha_k$に対して，縦$\alpha_k$×横$m(\set{x\in A}{f(x)=\alpha_k})$を考えて，和を考えたものが$f$のルベーグ積分というわけですね．
$f$が可測単関数なら，上で示した補題（単関数が可測関数であるための必要十分条件）から$\set{x\in A}{f(x)=\alpha_k}$は全て可測集合なので，これらの測度$m(\set{x\in A}{f(x)=\alpha_k})$は問題なく定義されますね．
具体例１（値１，２，３のみをとる関数）
関数
\begin{align*}f:[0,3]\to\R;x\mapsto\begin{cases}2&(0\le x<\frac{3}{2})\\3&(\frac{3}{2}\le x<2)\\1&(2\le x\le3)\end{cases}\end{align*}
に対して，
- $m(\set{x\in[0,3]}{f(x)=1})=m([3,5])=2$
- $m(\set{x\in[0,3]}{f(x)=2})=m([0,\frac{3}{2}))=\frac{3}{2}$
- $m(\set{x\in[0,3]}{f(x)=3})=m([\frac{3}{2},3))=\frac{3}{2}$
なので，$f$の$[0,3]$上のルベーグ積分は
\begin{align*}\int_{[0,3]}f(x)\,dx=1\times2+2\times\frac{3}{2}+3\times\frac{3}{2}=\frac{19}{2}\end{align*}
となります．
具体例２（ディリクレ関数）
ディリクレ関数
\begin{align*}f:\R\to\R;x\mapsto\begin{cases}1&(x\in\Q)\\0&(x\in\R\setminus\Q)\end{cases}\end{align*}
に対して，
- $m(\set{x\in\R}{f(x)=0})=m(\R\setminus\Q)=\infty$
- $m(\set{x\in\R}{f(x)=1})=m(\Q)=0$
なので，$f$の$\R$上のルベーグ積分は
\begin{align*}\int_{\R}f(x)\,dx=0\times\infty+1\times0=0\end{align*}
となります．
ディリクレ関数はあまりに不連続でリーマン積分不可能な関数ですから，この例からリーマン積分できない関数もルベーグ積分できる場合があることが分かりますね．
ルベーグ積分において$\pm\infty$は拡大実数で考えます．そのため，$0\times\infty$は０となります．
コメント