ルベーグ測度$m$の性質を考えるには,定義域であるルベーグ可測集合族$\mathcal{L}$にどのような集合が属しているのかを知っておきたいところです.
例えば,
- $\R$上の区間
- $\R$上の開集合
- $\R$上の閉集合
はいずれもルベーグ可測集合であることが証明できます.
一般に可測集合の和集合・共通部分も可測集合だったことと併せると,かなり多くの$\R$の部分集合がルベーグ可測集合であることが分かりますね.
この記事では
- $\R$上の区間・開集合・閉集合の可測性の証明
- ボレル集合族$\mathcal{B}$
を順に説明します.
「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
$\R$上の区間の可測性
例えば,右半開区間$[3,5)$は
\begin{align*}[3,5)=(-\infty,5)\cap[3,\infty)\end{align*}
と表されます.このように,全ての区間は無限区間$[a,\infty)$, $(a,\infty)$, $(-\infty,b]$, $(-\infty,b)$の形の区間の共通部分で表すことができます.
一般に可測集合の共通部分も可測集合だったので,上の4タイプの無限区間が全て可測であることが証明できれば,全ての区間が可測であることが分かりますね.
任意の区間$I\subset\R$はルベーグ可測集合である.
$a,b\in\R$に対して,無限区間$[a,\infty)$, $(a,\infty)$, $(-\infty,b]$, $(-\infty,b)$が全て可測であることを示せばよい.
まず,$I:=[a,\infty)$とし$I$が可測集合であることを示す.
任意に集合$X\subset\R$をとる.外測度$m^{*}$の定義の下限$\inf$の性質より,任意の$\epsilon>0$に対して,ある右半開区間の列$\{I_n\}$が存在して
\begin{align*}m^{*}(X)+\epsilon>\sum_{n=1}^{\infty}|I_n|\end{align*}
が成り立つ.ここで$J_n:=I\cap I_n$, $K_n:=I^c\cap I_n$ ($n=1,2,\dots$)とおくと,$\{J_n\}$と$\{K_n\}$はともに右半開区間の列で
\begin{align*}X\cap I\subset\bigcup_{n=1}^{\infty}J_n,\quad
X\cap I^c\subset\bigcup_{n=1}^{\infty}K_n\end{align*}
が成り立ち,$|I_n|=|J_n|+|K_n|$($n=1,2,\dots$)が成り立ちます.よって,
\begin{align*}\sum_{n=1}^{\infty}|I_n|
=\sum_{n=1}^{\infty}(|J_n|+|K_n|)
\ge m^{*}(X\cap I)+m^{*}(X\cap I^c)\end{align*}
が成り立つから$m^{*}(X)+\epsilon>m^{*}(X\cap I)+m^{*}(X\cap I^c)$を得る.
よって,$\epsilon$の任意性と併せて$m^{*}(X)\ge m^{*}(X\cap I)+m^{*}(X\cap I^c)$だから$I$は可測集合である.
同様に$(-\infty,b)$も可測集合である.さらに,$(a,\infty)=(-\infty,a]^c$, $(-\infty,b]=(b,\infty)^c$であり,一般に可測集合の補集合も可測集合だから$(a,\infty)$, $(-\infty,b]$も可測集合である.
$\R$上の開集合・閉集合の可測性
次に,開集合と閉集合の可測性を証明しましょう.
開集合の可測性
任意の開集合$A\subset\R$はルベーグ可測集合である.ただし,$\R$の標準位相空間である.
$A=\emptyset$なら$A$は開集合で可測集合である.よって,あとは$A\neq\emptyset$で示せばよい.
以下,高々可算個の開区間の列$\{I_n\}$の和集合が存在して,
\begin{align*}A=\bigcup_{n=1}^{\infty}I_n\end{align*}
と表せることを示す.
これが示されれば,一般に可測集合の可算和集合も可測集合だから,$\R$上の区間が可測集合であることと併せて$A$は可測集合と分かる.
ステップ1(開区間の族$\{I_n\}$の定義)
$A$は空でない開集合なので$A$に含まれる有理数は無限に存在するから,$A\cap\Q$は可算集合なので$A\cap\Q=\{a_1,a_2,\dots\}$とする.
任意の$a_n\in A\cap\Q$に対して,$(a_n-r,a_n+r)\subset A$を満たす$r>0$の上限の$\frac{1}{2}$を$r_n$とおく:
\begin{align*}r_n:=\sup\set{\frac{r}{2}>0}{(a_n-r,a_n+r)\subset A}.\end{align*}
さらに,このとき$I_n:=(a_n-r_n,a_n+r_n)$とする.
ステップ2($A=\bigcup_{n=1}^{\infty}I_n$の証明)
$I_n$の定義より$\bigcup\limits_{n=1}^{\infty}I_n\subset A$が成り立つ.
一方,任意に$a\in A$をとる.$A$は開集合だから,ある$\epsilon>0$が存在して$(a-\epsilon,a+\epsilon)\subset A$が成り立つ.
$\R$における$\Q$の稠密性から,ある$k\in\N$が存在して$a_k\in(a-\frac{\epsilon}{4},a+\frac{\epsilon}{4})\subset A$なので,$r_k$の定義より
\begin{align*}r_k\ge\frac{1}{2}\cdot\frac{3\epsilon}{4}=\frac{3\epsilon}{8}>\frac{\epsilon}{4}>|a-a_k|\end{align*}
が成り立つ.
よって,$a\in I_k$なので$a\in\bigcup\limits_{n=1}^{\infty}I_n$が成り立ち,$A\subset\bigcup\limits_{n=1}^{\infty}I_n$を得る.
開集合$A$が$A=\bigcup\limits_{n=1}^{\infty}I_n$と開区間の可算和で表されるから,$A$は可測集合である.
閉集合の可測性
一般に閉集合の補集合は開集合であることから,閉集合の可測性は直ちに示されます.
任意の閉集合$A\subset\R$はルベーグ可測集合である.ただし,$\R$の標準位相空間である.
閉集合の定義より$A^c$は開集合なので,いま示した定理より$A^c$は可測集合である.
また,一般に可測集合の補集合も可測集合だから,$A=(A^c)^c$は可測である.
ボレル集合族
可測空間は以下のように定義されるのでした.
集合$\Omega$を考える.$\mathcal{F}\subset\mathcal{P}(\Omega)$が次を満たすとき,$\mathcal{F}$を完全加法族(completely additive class)といい,組$(\Omega,\mathcal{F})$を可測空間(measurable space)という.
- $\Omega\in\mathcal{F}$
- $A\in\mathcal{F}\Ra A^c\in\mathcal{F}$
- $A_1,A_2,\dots\in\mathcal{F}$に対して$\bigcup\limits_{n=1}^{\infty}A_n\in\mathcal{F}$が成り立つ.
例えば,$\R$とルベーグ可測集合族$\mathcal{L}$の組$(\R,\mathcal{L})$は可測空間となるのでした.
集合$\Omega$が位相空間のとき,次のように完全加法族$\mathcal{F}$をとることができます.
位相空間$\Omega$に対して,$\Omega$上の開集合について和集合・共通部分・補集合を可算回とってできる集合全部からなる集合族$\mathcal{B}(\Omega)$は$\Omega$上の完全加法族である.すなわち,$(\Omega,\mathcal{B}(\Omega))$は可測空間である.
この定理の$\mathcal{B}(\Omega)$を$\Omega$上のボレル(Borel)集合族という.
上で示したように$\R$上の(自然な位相における)全ての開集合はルベーグ可測であり,ルベーグ可測集合の和集合,共通部分,補集合を可算回とっても可測でしたから,ボレル集合族$\mathcal{B}(\R)$は
\begin{align*}\mathcal{B}(\R)\subset\mathcal{L}\end{align*}
を満たすことが分かりますね.
なお,ルベーグ可測集合だがボレル可測でない集合が存在することが証明できます.つまり,$\mathcal{B}(\R)\neq\mathcal{L}$が成り立ちます.
また,$\mathcal{B}(\R)$は$\Omega$上の全ての開集合が属する最小の完全加法族ということもできます.
ルベーグ積分の文脈ではボレル集合族が登場する機会は多くありませんが,より広い測度論においてボレル集合族は重要な完全加法族です.

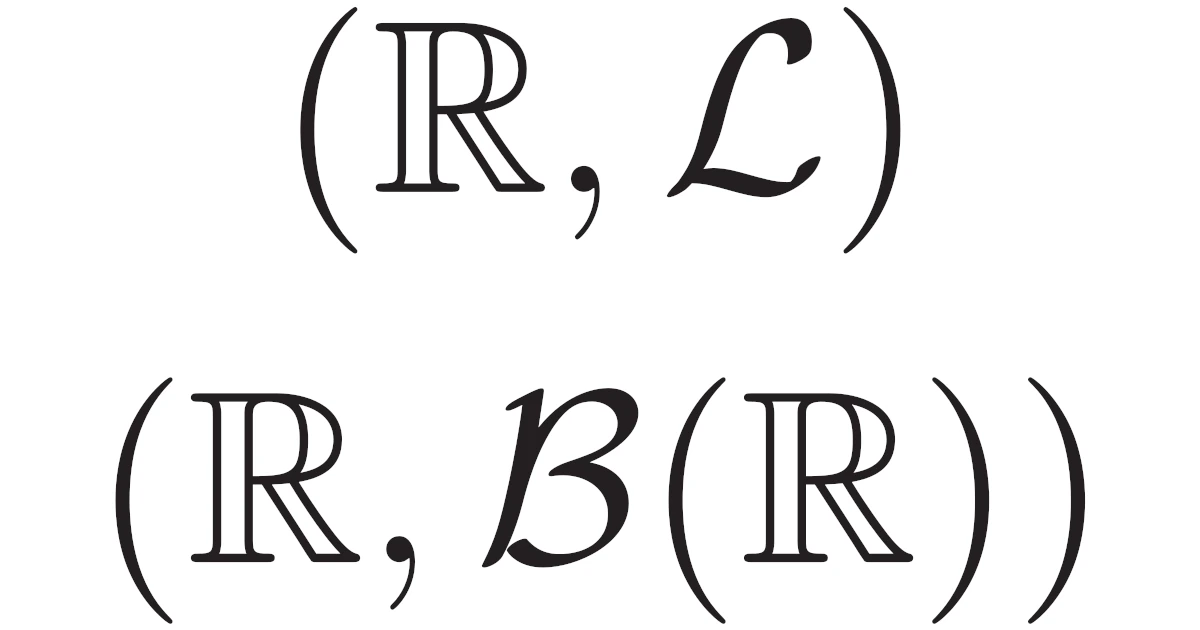


コメント