 偏微分方程式
偏微分方程式 シュレディンガー方程式の質量とエネルギー|保存則の証明
偏微分方程式の解が保存量を持つことはよくあり,それら保存量は偏微分方程式の解析で重要な手がかりとなります.この記事では,非線形シュレディンガー方程式の解uの質量MとエネルギーEが保存されることを説明します.
 偏微分方程式
偏微分方程式 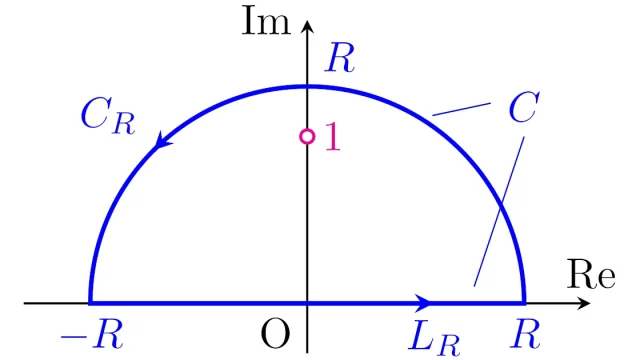 複素解析の基本
複素解析の基本 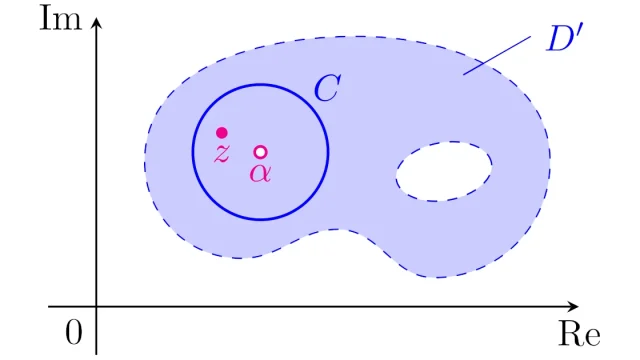 複素解析の基本
複素解析の基本 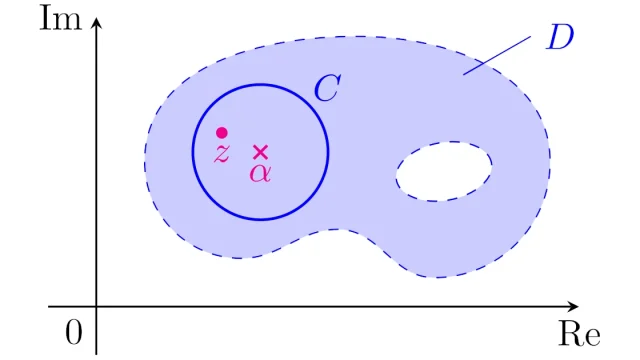 複素解析の基本
複素解析の基本 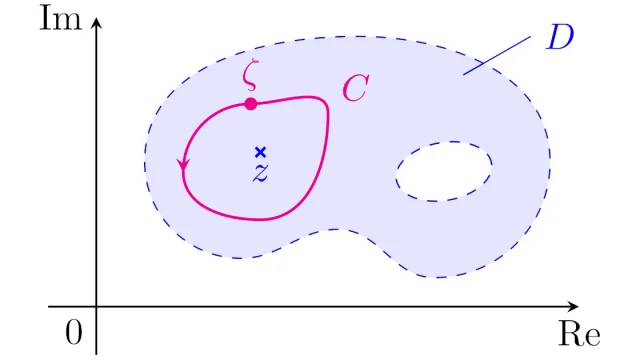 複素解析の基本
複素解析の基本 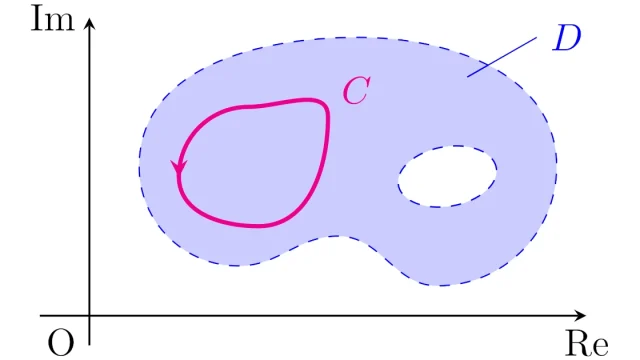 複素解析の基本
複素解析の基本 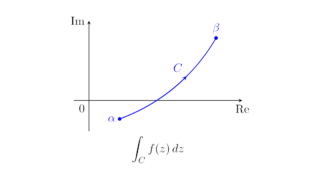 複素解析の基本
複素解析の基本 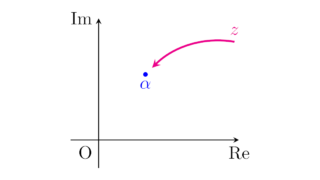 複素解析の基本
複素解析の基本 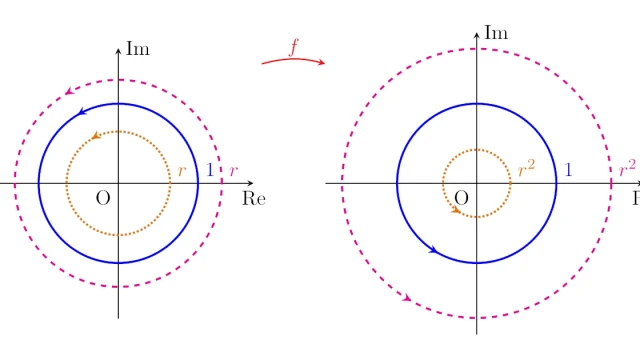 複素解析の基本
複素解析の基本  位相空間論
位相空間論