 線形代数学の基本
線形代数学の基本 行列Aの核Ker(A)の定義・考え方|求め方を例題から理解する
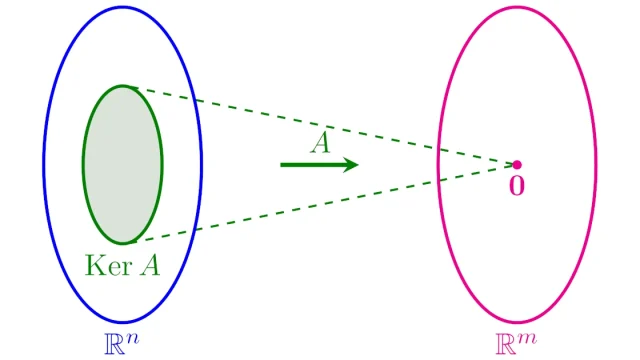
行列Aを左からベクトルにかけて零ベクトルとなるベクトルたち(連立方程式Ax=0の解)を全て集めてできる集合を行列Aの「核」といい,Ker(A)などと表します.行列の核は部分空間となることが知られており,重要な部分空間の1つです.
 線形代数学の基本
線形代数学の基本  データの記述
データの記述  線形代数学の基本
線形代数学の基本  線形代数学の基本
線形代数学の基本 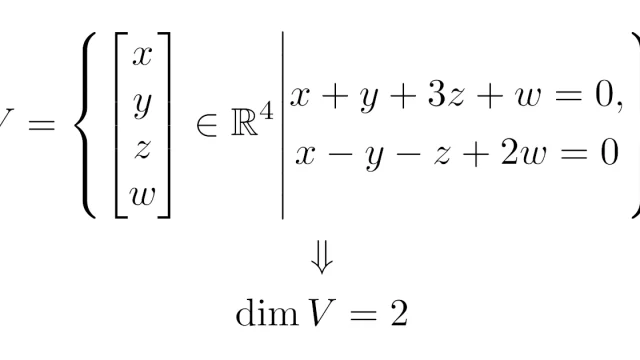 線形代数学の基本
線形代数学の基本 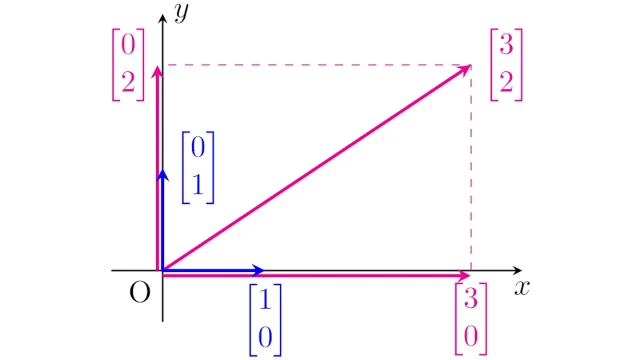 線形代数学の基本
線形代数学の基本 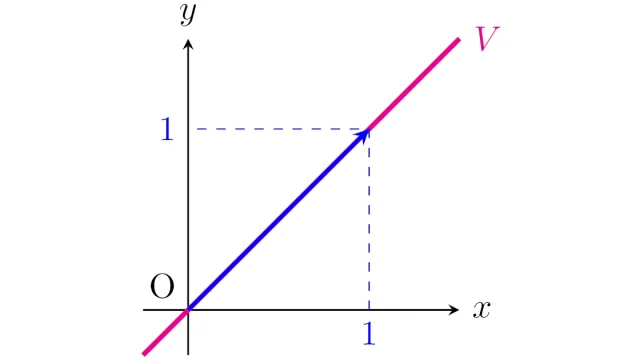 線形代数学の基本
線形代数学の基本 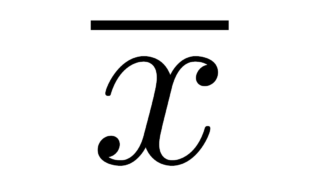 データの記述
データの記述 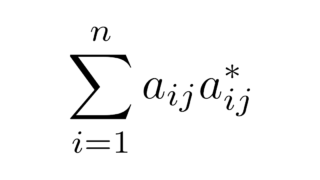 線形代数学の基本
線形代数学の基本 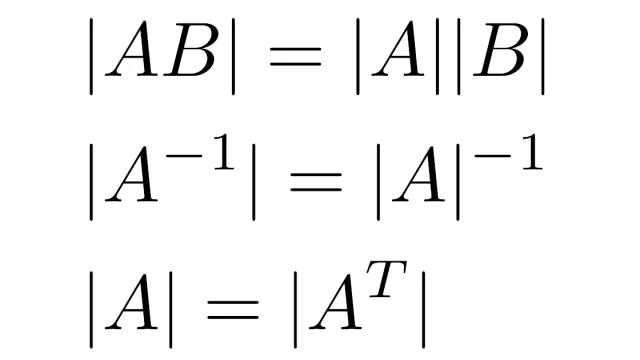 線形代数学の基本
線形代数学の基本