 複素解析の基本
複素解析の基本 ローラン展開はテイラー展開の進化形!留数定理の一歩前
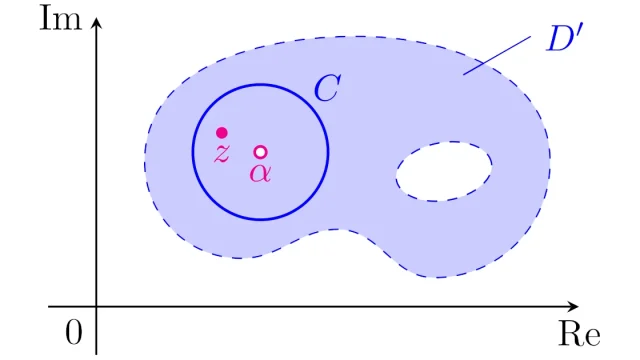
αの近くで微分可能な複素関数は「ローラン展開」することができ,ローラン展開はテイラー展開の拡張ということができます.また,複素解析の重要定理である「留数定理」を考えるためには欠かせないものとなっています.
 複素解析の基本
複素解析の基本 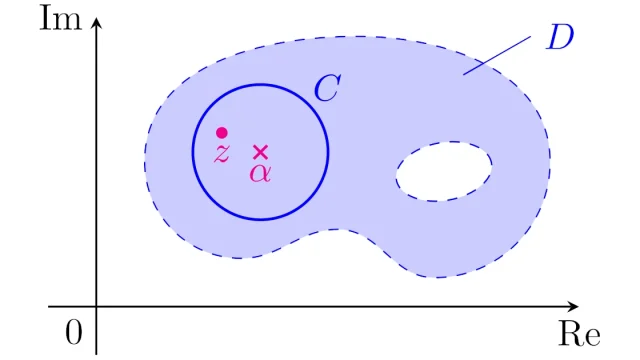 複素解析の基本
複素解析の基本 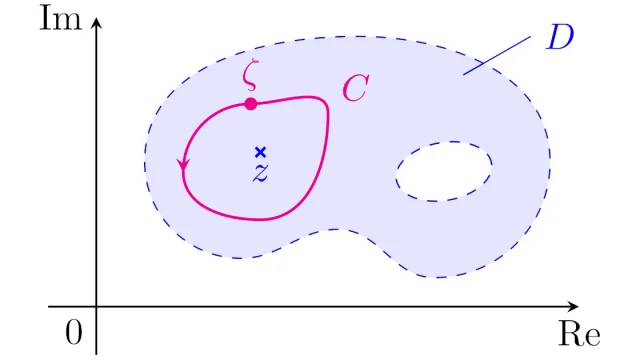 複素解析の基本
複素解析の基本 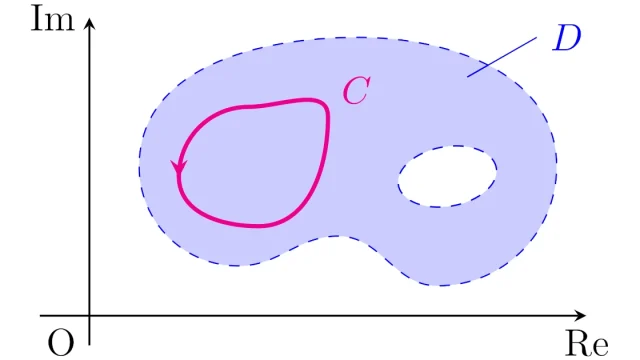 複素解析の基本
複素解析の基本 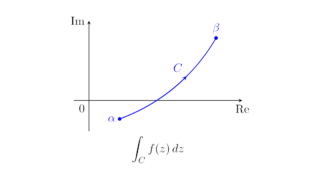 複素解析の基本
複素解析の基本  複素解析の基本
複素解析の基本 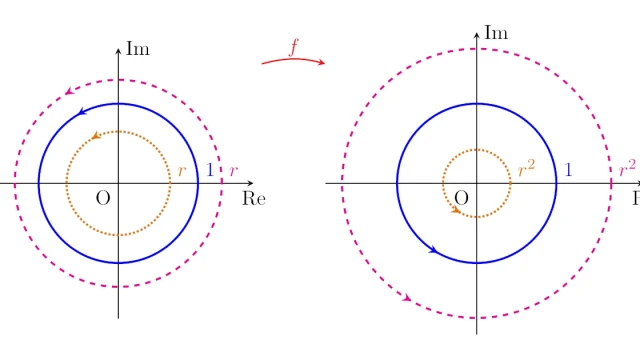 複素解析の基本
複素解析の基本 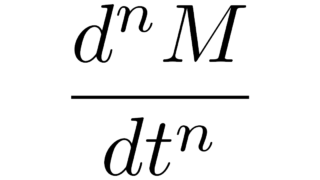 確率論
確率論 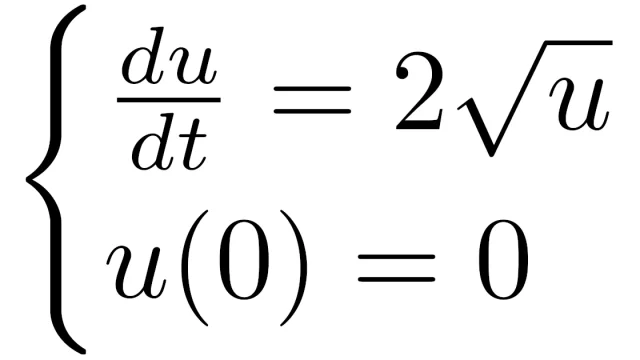 常微分方程式
常微分方程式 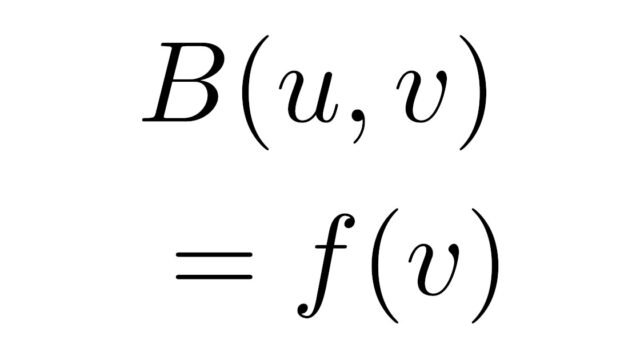 偏微分方程式
偏微分方程式