2026年度の京都大学 理学研究科 数学・数理解析専攻の大学院入試問題の基礎科目の解答の方針と解答例です.
問題は7題あり
- 数学系は第1〜6問を
- 数理解析系は第1〜5問と,第6,7問から1問を選択して
解答します.試験時間は3時間30分です.この記事では,第1〜7問について解説しています.
ただし,公式に採点基準などは発表されていないため,本稿の解答が必ずしも正解になるとは限りません.ご注意ください.
また,十分注意して解答を作成していますが,論理の飛躍・誤りが残っている場合があります.
なお,過去問は京都大学の数学教室の過去問題のページから入手できます.
第1問(微分積分学)
集合$D$を
\begin{align*}D=\set{(x,y)\in\R^2}{x>0,\ 0\le y\le x^2}\end{align*}
と定める.このとき,次の広義積分
\begin{align*}\iint_{D}\frac{dxdy}{(x^3+y^3)^\alpha}\end{align*}
が収束するような実数$\alpha$の範囲を求めよ.
広義積分が収束するための条件を求める問題です.
解答の方針とポイント
被積分関数の分母が$(x^2+y^2)^\beta$の形であれば極座標変換により解けそうですね.
答えの予想
本問の積分$\iint_{D}\frac{dxdy}{(x^3+y^3)^\alpha}$は
- 積分領域$D$が非有界
- 原点$(0,0)$で被積分関数が定義されていない(境界点$(0,0)$が積分領域$D$に属さない)
という2通りの意味で広義積分になっています.
答えのアタリをつけるために,被積分関数が$\frac{1}{(x^2+y^2)^\beta}$の積分を考えてみましょう.積分領域が
- $E_1=\set{(x,y)\in\R^2}{1\le x^2+y^2}$
- $E_2=\set{(x,y)\in\R^2}{0<x^2+y^2\le1}$
の場合には,極座標変換$x=r\cos{\theta}$, $y=r\sin{\theta}$により,それぞれ
\begin{align*}&\iint_{E_1}\frac{dxdy}{(x^2+y^2)^\beta}=\lim_{n\to\infty}\int_{1}^{n}\bra{\int_{0}^{2\pi}r^{1-2\beta}\,d\theta}\,dr,
\\&\iint_{E_2}\frac{dxdy}{(x^2+y^2)^\beta}=\lim_{n\to\infty}\int_{1/n}^{1}\bra{\int_{0}^{2\pi}r^{1-2\beta}\,d\theta}\,dr\end{align*}
となり,前者は$\beta>1$のときに収束し,後者は$\beta<1$のときに収束することが分かります.
さて,本問では被積分関数は$\frac{1}{(x^3+y^3)^\alpha}$ですが,遠方での積分が収束するオーダーは$\frac{1}{(x^2+y^2)^\beta}$の遠方での積分の場合と同じく$\frac{3\alpha}{2}>1$になっていそうです.
一方,原点では積分領域が「速く」狭まっているため,被積分関数が増大していても積分は発散しにくくなっていることが予想できます.
そのため,遠方での積分から$\alpha>\frac{2}{3}$が得られ,原点付近の積分から$\alpha<C$($C>\frac{2}{3}$)の形の評価が得られ,$\frac{2}{3}<\alpha<C$となりそうですね.
$x^2+y^2$と$x^3+y^3$のオーダー
いまの答えの予想の考察では,直観的に$(x^2+y^2)^{3/2}$は3次式$x^3+y^3$と同程度の増大と減衰をもつとして考えていました,実際,
\begin{align*}(x^3+y^3)^2\le3(x^2+y^2)^3,&&
(x^2+y^2)^3\le7(x^3+y^3)^2\end{align*}
ですから,$\frac{1}{\sqrt{7}}(x^2+y^2)^{3/2}\le x^3+y^3\le\sqrt{3}(x^2+y^2)^{3/2}$なので,2つの広義積分
\begin{align*}\iint_{D}\frac{dxdy}{(x^3+y^3)^\alpha},&&
\iint_{D}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}\end{align*}
の収束・発散が一致することが分かります.そのため,$\iint_{D}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}$が収束するような$\alpha$の条件を求めれば良いですね.
遠方での積分が収束する条件
本問の積分で面倒なところは,積分領域が極座標変換と相性があまりよくない点です.
ところが,積分$\iint_{D}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}$が遠方での収束・発散を決めるのは点$(x,y)$の原点からの距離$r=\sqrt{x^2+y^2}$に関する減衰度なので,遠方での積分では積分領域を多少広くしたり狭くしたりしても偏角の範囲が変化するだけで,$\alpha$の収束条件は変化しないと考えられます.
そこで,遠方$D_1=\set{(x,y)\in D}{1\le x^2+y^2}$上の積分を
- $D_1$より小さい$D_{1-}=\set{(x,y)\in D_1}{0\le y\le\frac{1}{\sqrt{3}}x,\ 1\le x^2+y^2}$上の積分
- $D_1$より大きい$D_{1+}=\set{(x,y)\in\R^2}{0\le x,\ 0\le y,\ 1\le x^2+y^2}$上の積分
の両方で挟み,これらの積分が収束する$\alpha$の範囲が一致することを示すことで,遠方での積分が収束する$\alpha$の範囲を求められそうですね.
原点付近での積分が収束する条件
原点付近では,積分領域の狭まり加減が収束・発散に影響しそうですから,遠方での考え方のように積分領域を変化させるのは良くなさそうです.
しかし,$(x,y)\in D$が$x\le1$を満たすときは
\begin{align*}x^2\le x^2+y^2\le x^2+x^4\le2x^2\end{align*}
ですから,原点付近の積分では$\frac{1}{x^{3\alpha}}$の積分が収束する$\alpha\in\R$の範囲に一致しますね.
いまの議論は$x^3+y^3$についても同様に成り立つので,原点付近での積分が収束する条件は$\frac{1}{(x^3+y^3)^\alpha}$のままでも得られます.
解答例
関数$(x,y)\mapsto(x^3+y^3)^{\alpha}$は$D$上連続だから,$D_1=\set{(x,y)\in D}{1\le x^2+y^2}$, $D_2=\set{(x,y)\in D}{0<x\le1}$として,
\begin{align*}\iint_{D_1}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}},\quad\iint_{D_2}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}\end{align*}
がともに収束する実数$\alpha$の範囲を求めればよく,以下この範囲が$\frac{2}{3}<\alpha<1$であることを示す.
$D_1$上の積分が収束する条件
$(x,y)\in D_1$のとき
\begin{align*}(x^3+y^3)^2&=x^6+2x^3y^3+y^6
\\&\le3(x^6+y^6)\le3(x^2+y^2)^3,
\\(x^2+y^2)^3&=x^6+3x^4y^2+3x^2y^4+y^6
\\&\le7(x^6+y^6)\le7(x^3+y^3)^2\end{align*}
なので,求める$\alpha\in\R$の範囲は$\iint_{D_1}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}$が収束する$\alpha\in\R$の範囲に一致する.
\begin{align*}&D_{1,+}=\set{(x,y)\in\R^2}{0\le x,\ 0\le y,\ 1\le x^2+y^2},
\\&D_{1,-}=\set{(x,y)\in\R^2}{0\le y\le\frac{1}{\sqrt{3}}x,\ 1\le x^2+y^2}\end{align*}
とすると,$D_{1,-}\subset D_1\subset D_{1,+}$である.また,複号同順で
\begin{align*}D_{1,n\pm}=\set{(x,y)\in D_{1,\pm}}{x^2+y^2\le n^2}\end{align*}
とおくと,
\begin{align*}&\iint_{D_{1,\pm}}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}
=\lim_{n\to\infty}\iint_{D_{1,n\pm}}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}\end{align*}
であり,極座標変換$x=r\cos{\theta}$, $y=r\sin{\theta}$により
\begin{align*}&\iint_{D_{1,n+}}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}
=\int_{0}^{\pi/2}\bra{\int_{1}^{n}\frac{r}{r^{3\alpha}}\,dr}\,d\theta
\\&=\begin{cases}\frac{\pi}{2(2-3\alpha)}(n^{2-3\alpha}-1),&\alpha\neq\frac{2}{3},\\
\frac{\pi}{2}\log{n},&\alpha=\frac{2}{3},\end{cases}
\\&\iint_{D_{1,n-}}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}
=\int_{0}^{\pi/6}\bra{\int_{1}^{n}\frac{r}{r^{3\alpha}}\,dr}\,d\theta
\\&=\begin{cases}\frac{\pi}{6(2-3\alpha)}(n^{2-3\alpha}-1),&\alpha\neq\frac{2}{3},\\
\frac{\pi}{6}\log{n},&\alpha=\frac{2}{3}\end{cases}\end{align*}
なので,$\iint_{D_{1,+}}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}$, $\iint_{D_{1,-}}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}$が収束するための$\alpha$の必要十分条件は,ともに
\begin{align*}2-3\alpha<0\iff \frac{2}{3}<\alpha\end{align*}
である.よって,$D_{1,-}\subset D_1\subset D_{1,+}$と併せて,$\iint_{D_1}\frac{dxdy}{(x^2+y^2)^{3\alpha/2}}$が収束するための$\alpha$の必要十分条件は$\alpha>\frac{2}{3}$である.
$D_2$上の積分が収束する条件
$(x,y)\in D_2$のとき
\begin{align*}x^3\le x^3+y^3\le x^3+x^6\le2x^3\end{align*}
なので,$\iint_{D_2}\frac{dxdy}{(x^3+y^3)^{\alpha}}$が収束する$\alpha\in\R$の範囲は$\iint_{D_2}\frac{dxdy}{x^{3\alpha}}$が収束する$\alpha\in\R$の範囲に一致する.
$D_{2,n}=\set{(x,y)\in D_2}{\frac{1}{n}\le x}$とすると,
\begin{align*}&\iint_{D_2}\frac{dxdy}{x^{3\alpha}}=\lim_{n\to\infty}\iint_{D_{2,n}}\frac{dxdy}{x^{3\alpha}}\end{align*}
であり,
\begin{align*}&\iint_{D_{2,n}}\frac{dxdy}{x^{3\alpha}}
=\int_{1/n}^{1}\bra{\int_{0}^{x^2}\frac{1}{x^{3\alpha}}\,dy}\,dx
\\&=\int_{1/n}^{1}x^{2-3\alpha}\,dx
=\begin{cases}\frac{1}{3-3\alpha}(1-n^{3\alpha-3}),&\alpha\neq1,\\
\log{n},&\alpha=1\end{cases}\end{align*}
なので,$\iint_{D_2}\frac{dxdy}{(x^3+y^3)^{\alpha}}$が収束するための$\alpha$の必要十分条件は
\begin{align*}3\alpha-3<0\iff\alpha<1\end{align*}
である.
第2問(線形代数学)
$a$, $b$を実数とする.行列
\begin{align*}\pmat{a&a&b&b\\a&a&-b&b\\b&b&a&a\\-b&b&-a&a}\end{align*}
の階数を求めよ.
$a$, $b$がどのようなときに行列のランクがどうなるかを分類する問題です.
解答の方針とポイント
行列に(行)基本変形を施して階段行列にできれば,そのときの主成分の個数がランク(階数)ですね.
そのため,(行)基本変形でうまく消えそうなところを見つけるのがポイントです
ただし,成分が文字のときは,その文字が0である可能性に注意する必要があります.
解答例
階数を求める行列を$A$とおく:$A=\sbmat{a&a&b&b\\a&a&-b&b\\b&b&a&a\\-b&b&-a&a}$.以下,変形はすべて行基本変形である.
$a=b=0$のとき,$A$は零行列だから$\rank{A}=0$である.$a=0$かつ$b\neq0$のとき,
\begin{align*}A&=\bmat{0&0&b&b\\0&0&-b&b\\b&b&0&0\\-b&b&0&0}\to\bmat{1&1&0&0\\0&2&0&0\\0&0&1&1\\0&0&0&2}\end{align*}
となるから$\rank{A}=4$である.$b=0$かつ$a\neq0$のとき,
\begin{align*}A&=\bmat{a&a&0&0\\a&a&0&0\\0&0&a&a\\0&0&-a&a}\to\bmat{1&1&0&0\\0&0&1&1\\0&0&0&2\\0&0&0&0}\end{align*}
となるから$\rank{A}=3$である.$ab\neq0$のとき,
\begin{align*}A&\to\bmat{a&a&b&b\\0&0&-2b&0\\b&b&a&a\\0&2b&0&2a}\to\bmat{a&a&b&b\\0&0&1&0\\0&0&a-\frac{b^2}{a}&a-\frac{b^2}{a}\\0&b&0&a}
\\&\to\bmat{a&a&b&b\\0&b&0&a\\0&0&1&0\\0&0&0&\frac{a^2-b^2}{a}}\end{align*}
だから,$\rank{A}=\begin{cases}3,&a=\pm b,\\4,&a\neq\pm b\end{cases}$である.
以上をまとめて
\begin{align*}\rank{A}=\begin{cases}0,&a=b=0,\\3,&(b=0\ \text{かつ}\ a\neq0)\ \text{または}\ a=\pm b\neq0,\\4,&\mrm{それ以外}\end{cases}\end{align*}
である.
第3問(線形代数学)
$n$を正の整数とし,複素$n$次正方行列全体のなす複素ベクトル空間を$M_n(\C)$とする.$X\in M_n(\C)$に対して,$M_n(\C)$の部分ベクトル空間$V_X$を
\begin{align*}V_X=\set{A\in M_n(\C)}{AX=XA}\end{align*}
で定める.このとき,$\set{\dim{V_X}}{X\in M_n(\C)}$の最小値が$n$になることを示せ.ここで$\dim{V_X}$は$V_X$の複素ベクトル空間としての次元を表す.
特定の正方行列$X$と可換な行列がなす線形空間$V_X$の次元について,$X$を様々にとるときの次元$\dim{V_X}$の最小値が$n$であることを示す問題です.
解答の方針とポイント
最小値が$n$であることを示すので,任意の$X\in M_n(\C)$に対して$\dim{V_X}\ge n$であることと,$\dim{V_X}=n$となる$X\in M_n(\C)$が存在することを示せば良いですね.
ジョルダン標準形
複素正方行列$A$は対角化可能とは限りませんが,ジョルダン標準形は必ずもちます.
任意の複素正方行列$X$はジョルダン標準形をもつ.すなわち,ある複素正則行列$P$が存在して$P^{-1}XP$がジョルダン行列となる.
このときのジョルダン行列$P^{-1}XP$を$X$のジョルダン標準形といいますね.
そこで,$X\in M_n(\C)$のジョルダン標準形を$J$とすると,$A\in M_n(\C)$に対して
\begin{align*}AX=XA
&\iff A(PJP^{-1})=(PJP^{-1})A
\\&\iff (P^{-1}AP)J=J(P^{-1}AP)\end{align*}
となるので,
\begin{align*}A\in V_X\iff P^{-1}AP\in V_J\end{align*}
と分かります.よって,$V_X\cong V_J$なので,$\dim{V_X}=\dim{V_J}$が成り立ちます.したがって,もとよりジョルダン行列$X\in M_n(\C)$に対して$\dim{V_X}$を考えていれば良いことが分かります.
数学・数理解析専攻の大学院入試ではジョルダン標準形は頻出なので,意識しておくとよいでしょう.
ジョルダン細胞と可換な行列
最初から$X\in M_n(\C)$をジョルダン行列で考えてよいとはいっても,まだ様子はよく分かりません.このようなときは,簡単な例からでよいので,きちんと実験して様子を掴むことが大切です.
たとえば,簡単なジョルダン行列であるジョルダン細胞
\begin{align*}X=J_3(2)=\bmat{2&1&0\\0&2&1\\0&0&2}\end{align*}
に対して$AX=XA$を満たす$A$を実際に求めると$A=\bmat{a&b&c\\0&a&b\\0&0&a}$($a,b,c\in\C$)となり,$\dim{V_X}=3$であることが分かります.
一般にジョルダン行列$X$はジョルダン細胞を用いて
\begin{align*}X&=J_{n_1}(\lambda_1)\oplus J_{n_2}(\lambda_2)\oplus\dots\oplus J_{n_r}(\lambda_r)
\\&=\bmat{J_{n_1}(\lambda_1)&O&\dots&O\\O&J_{n_2}(\lambda_2)&\ddots&\vdots\\\vdots&\ddots&\ddots&O\\O&\dots&O&J_{n_r}(\lambda_r)}\end{align*}
の形で表される行列なので,上の$X=J_3(2)$の考察と併せて$n$個の任意定数をもつ行列$A$と可換であることが分かり,$\dim{V_X}\ge n$が得られます.
また,極端なジョルダン行列である対角行列で実験をすると,対角成分が全て異なる対角行列$X$で$\dim{V_X}=n$となることがみてとれます.
繰り返すようですが,様子がよく分からない問題で具体的に対象を決めて実験することはとても大切です.
解答例
任意の$X\in M_n(\C)$に対して$\dim{V_X}\ge n$が成り立つことを示し,$\dim{V_X}=n$となる$X\in M_n(\C)$が存在することを示せばよい.
$\dim{V_X}\ge n$の証明
任意に$X\in M_n(\C)$をとる.$n$次の$\lambda\in\C$に関するジョルダン細胞を$J_n(\lambda)$と表す.$X$のジョルダン標準形を
\begin{align*}J=\bigoplus_{k=1}^{r}J_{n_k}(\lambda_k)\end{align*}
とし,$P^{-1}XP=J$なる$n$次正則行列$P$をとると,$A\in M_n(\C)$に対して
\begin{align*}AX=XA
&\iff (P^{-1}AP)(P^{-1}XP)=(P^{-1}XP)(P^{-1}AP)
\\&\iff (P^{-1}AP)J=J(P^{-1}AP)\end{align*}
が成り立つ.よって,写像
\begin{align*}\phi:V_X\to V_J;A\mapsto P^{-1}AP\end{align*}
は同型なので,$\dim{V_X}=\dim{V_J}$である.
ここで,任意の$k\in\{1,2,\dots,r\}$に対して,$a_{k1},a_{k2},\dots,a_{kn_k}\in\C$として
\begin{align*}A_k=\sum_{\ell=1}^{n_k}a_{k\ell}J_{n_k}(0)^{\ell-1}\end{align*}
とおくと,$A_k$は$J_{n_k}(0)$の多項式なので$A_kJ_{n_k}(0)=J_{n_k}(0)A_k$だから
\begin{align*}A_kJ_{n_k}(\lambda_k)&=A_k(\lambda_kI_{n_k}+J_{n_k}(0))
\\&=(\lambda_kI_{n_k}+J_{n_k}(0))A_k=J_{n_k}(\lambda_k)A_k\end{align*}
が成り立つ.よって,
\begin{align*}\bra{\bigoplus_{k=1}^{r}A_k}J
=\bigoplus_{k=1}^{r}(A_kJ_{n_k}(\lambda_k))
=\bigoplus_{k=1}^{r}(J_{n_k}(\lambda_k)A_k)
=J\bra{\bigoplus_{k=1}^{r}A_k}\end{align*}
だから,$\bigoplus\limits_{k=1}^{r}A_k\in V_J$である.$\bigoplus\limits_{k=1}^{r}A_k$は任意定数を$n$個もつから$\dim{V_X}=\dim{V_J}\ge n$が従う.
$\dim{V_X}=n$となる$X\in M_n(\C)$の具体例
$X=\diag{(1,2,\dots,n)}$とすると,$A=(a_{ij})\in M_n(\C)$に対して$AX=\{ja_{ij}\}$, $XA=\{ia_{ij}\}$だから
\begin{align*}AX=XA
&\iff \forall i,j\in\{1,2,\dots,n\}\quad ja_{ij}=ia_{ij}
\\&\iff a_{ij}=0\quad(i\neq j;i,j\in\{1,2,\dots,n\})
\\&\iff \text{$A$は対角行列}\end{align*}
である.よって,
\begin{align*}\dim{V_X}=\dim\set{\diag{(a_1,a_2,\dots,a_n)}\in M_n(\C)}{a_1,a_2,\dots,a_n\in\C}=n\end{align*}
である.
第4問(微分積分学)
以下で,次の条件
\begin{align*}&\limsup_{n\to\infty}a_n=3,&\liminf_{n\to\infty}a_n=0,
\\&\limsup_{n\to\infty}b_n=7,&\liminf_{n\to\infty}b_n=1\end{align*}
を満たす実数列$\{a_n\}_{n=1}^{\infty}$と$\{b_n\}_{n=1}^{\infty}$について考える.
- $\limsup\limits_{n\to\infty}|a_n-b_n|$のとり得る値の最大値と最小値を求めよ.さらに,これらの最大値と最小値を与える$(\{a_n\}_{n=1}^{\infty},\{b_n\}_{n=1}^{\infty})$の例をそれぞれ1つ挙げよ.
- $\liminf\limits_{n\to\infty}|a_n-b_n|$のとり得る値の最大値と最小値を求めよ.さらに,これらの最大値と最小値を与える$(\{a_n\}_{n=1}^{\infty},\{b_n\}_{n=1}^{\infty})$の例をそれぞれ1つ挙げよ.
上極限と下極限が異なる数列$\{a_n\}$と$\{b_n\}$の差の上極限と下極限の最大・最小問題です.
解答の方針とポイント
条件を満たす数列$\{a_n\}$, $\{b_n\}$をいくつか具体的に考えれば答えは自ずと分かりますが,それをきちんと示せるかが鍵です.
数列$\{a_n\}$, $\{b_n\}$の典型例
実数列$\{a_n\}$に対して,
\begin{align*}\lim_{n\to\infty}\Bigl(\sup_{p\ge n}a_p\Bigr),\quad
\lim_{n\to\infty}\Bigl(\inf_{p\ge n}a_p\Bigr)\end{align*}
をそれぞれ実数列$\{a_n\}$の上極限,下極限といい,$\limsup\limits_{n\to\infty}a_n$, $\liminf\limits_{n\to\infty}a_n$と表す.
上極限と下極限が異なる典型的な数列は$\{(-1)^n\}$で,
\begin{align*}\limsup_{n\to\infty}(-1)^n=1,\quad\liminf_{n\to\infty}(-1)^n=-1\end{align*}
ですね.この例のように考えると,本問の数列$\{a_n\}$, $\{b_n\}$の典型的な例として
\begin{align*}a_n=\begin{cases}0,&n=1,3,5,\dots,\\3,&n=2,4,6,\dots,\end{cases}\quad
b_n=\begin{cases}1,&n=1,3,5,\dots,\\7,&n=2,4,6,\dots\end{cases}\end{align*}
が挙げられますね.
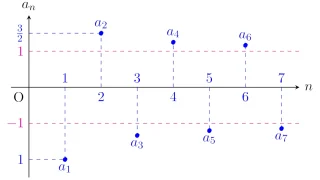
差の絶対値の$|a_n-b_n|$の上極限の最大値・最小値
任意の$\epsilon>0$に対して,$n$が十分大きければ
\begin{align*}0-\epsilon<a_n<3+\epsilon,\quad
1-\epsilon<b_n<7+\epsilon\end{align*}
となります.数列$\{a_n\}$は3付近,0付近の値を無限に取り続け,数列$\{b_n\}$は7付近,1付近の値を無限に取り続けるので,
- $\sup\limits_{k\ge n}|a_k-b_k|$は最大で$7-0=7$程度
- $\sup\limits_{k\ge n}|a_k-b_k|$は最小で$7-3=4$程度
と言えそうですね.よって,$4\le\limsup\limits_{n\to\infty}|a_n-b_n|\le7$を示し,左右の不等号それぞれで等号が成り立つような数列$\{a_n\}$, $\{b_n\}$の例を見つければよいですね.
差の絶対値の$|a_n-b_n|$の下極限の最大値・最小値
$a_n=b_n$となるような$n\in\N$が無限に存在すれば,任意の$n\in\N$に対して$\inf\limits_{k\ge n}|a_k-b_k|=0$ですから,$\liminf\limits_{n\to\infty}|a_n-b_n|=0$となります.
また,数列$\{a_n\}$は3付近,0付近の値を無限に取り続け,数列$\{b_n\}$は7付近,1付近の値を無限に取り続けるので,$\inf\limits_{k\ge n}|a_k-b_k|$は最大で$3-1=2$程度と言えそうですね.
よって,$0\le\liminf\limits_{n\to\infty}|a_n-b_n|\le2$を示し,左右の不等号それぞれで等号が成り立つような数列$\{a_n\}$, $\{b_n\}$の例を見つければよいですね.
解答例
任意に$\epsilon\in(0,1)$をとる.仮定より,ある$N_i\in\N$($i=1,2,3,4$)が存在して
\begin{align*}&n>N_1\Ra\abs{\sup_{k\ge n}a_k-3}<\epsilon,&&n>N_2\Ra\abs{\inf_{k\ge n}a_k}<\epsilon,
\\&n>N_3\Ra\abs{\sup_{k\ge n}b_k-7}<\epsilon,&&n>N_4\Ra\abs{\inf_{k\ge n}b_k-1}<\epsilon\end{align*}
が成り立つ.$N=\max\{N_1,N_2,N_3,N_4\}$とおく.
(1)の解答
以下,すべて$n>N$とする.$\limsup\limits_{n\to\infty}|a_n-b_n|=\lim\limits_{n\to\infty}\bra{\sup\limits_{k\ge n}|a_k-b_k|}$であり,$n>N$なら
\begin{align*}\sup_{k\ge n}|a_k-b_k|&\ge\sup_{k\ge n}(b_k-a_k)\ge\sup_{k\ge n}\bra{b_k+\inf_{k\ge n}(-a_k)}
\\&=\sup_{k\ge n}b_k+\inf_{k\ge n}(-a_k)=\sup_{k\ge n}b_k-\sup_{k\ge n}a_k\ge4-2\epsilon\end{align*}
が成り立つ.
一方,$-\epsilon<a_n<3+\epsilon$かつ$1-\epsilon<b_n<7+\epsilon$だから,$|a_n-b_n|<7+2\epsilon$となるから,$\sup\limits_{k\ge n}|a_k-b_k|\le7+2\epsilon$が成り立つ.
よって,$4-2\epsilon\le\sup\limits_{k\ge n}|a_k-b_k|\le7+2\epsilon$が従い,極限$n\to\infty$をとり,$\epsilon$の任意性と併せて$4\le\limsup\limits_{n\to\infty}|a_n-b_n|\le7$を得る.
ここで,条件を満たす数列$\{a_n\}$, $\{b_n\}$として
\begin{align*}a_n=\frac{3}{2}+\frac{3}{2}(-1)^n,\quad
b_n=4+3(-1)^n\quad\dots(*)\end{align*}
をとると,
\begin{align*}|a_n-b_n|=\frac{5}{2}+\frac{3}{2}(-1)^{n}\end{align*}
なので,任意の$n\in\N$に対して$\sup\limits_{k\ge n}|a_k-b_k|=4$だから$\limsup\limits_{n\to\infty}|a_n-b_n|=4$である.また,
\begin{align*}a_n=\frac{3}{2}+\frac{3}{2}(-1)^n,\quad
b_n=4+3(-1)^{n+1}\quad\dots(**)\end{align*}
をとると,
\begin{align*}|a_n-b_n|=\abs{\frac{5}{2}+\frac{9}{2}(-1)^{n+1}}=\frac{9}{2}+\frac{5}{2}(-1)^{n+1}\end{align*}
なので,任意の$n\in\N$に対して$\sup\limits_{k\ge n}|a_k-b_k|=7$だから$\limsup\limits_{n\to\infty}|a_n-b_n|=7$である.
以上より,$\limsup\limits_{n\to\infty}|a_n-b_n|$のとり得る値について,$(*)$のとき最小値4をとり,$(**)$のとき最大値7をとる.
(2)の解答
以下,すべて$n>N$とする.任意の$n\in\N$に対して$|a_n-b_n|\ge0$だから,$\liminf\limits_{n\to\infty}|a_n-b_n|\ge0$を得る.
一方,$|b_n-1|<\epsilon$を満たす$n\in\N$は無限に存在し,$|b_n-1|<\epsilon$を満たす$n$に対して,$-\epsilon<a_n<3+\epsilon$と併せて,$|a_n-b_n|\le2+2\epsilon$が成り立つ.
よって,$\inf\limits_{k\ge n}|a_k-b_k|\le2+2\epsilon$が従い,両辺で極限$n\to\infty$をとり,$\epsilon$の任意性と併せて$\liminf\limits_{n\to\infty}|a_n-b_n|\le2$を得る.
ここで,条件を満たす数列$\{a_n\}$, $\{b_n\}$として
\begin{align*}\begin{aligned}&a_n=\begin{cases}\frac{3}{2}+\frac{3}{2}(-1)^n,&n\in\N\setminus2^\N,\\2,&n\in2^\N,\end{cases}
\\&b_n=\begin{cases}4+3(-1)^n,&n\in\N\setminus2^\N,\\2,&n\in2^\N\end{cases}\end{aligned}\quad\dots(***)\end{align*}
をとると,任意の$n\in\N$に対して$|a_{2^n}-b_{2^n}|=0$なので,$\inf\limits_{k\ge n}|a_k-b_k|=0$だから$\liminf\limits_{n\to\infty}|a_n-b_n|=0$である.また,(1)の$(**)$をとると
\begin{align*}|a_n-b_n|=\frac{9}{2}+\frac{5}{2}(-1)^{n+1}\end{align*}
なので,任意の$n\in\N$に対して$\inf\limits_{k\ge n}|a_k-b_k|=2$だから$\liminf\limits_{n\to\infty}|a_n-b_n|=2$である.
以上より,$\liminf\limits_{n\to\infty}|a_n-b_n|$のとり得る値について,$(***)$のとき最小値0をとり,$(**)$のとき最大値2をとる.
第5問(複素解析学)
$u(x,y)$は$\R^2\setminus\{(0,0)\}$上の実数値$C^2$級関数であり,
\begin{align*}\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0\end{align*}
が$\R^2\setminus\{(0,0)\}$上で成り立つとする.さらに正の定数$C$が存在して,不等式
\begin{align*}\abs{\frac{\partial u}{\partial x}(x,y)}+\abs{\frac{\partial u}{\partial y}(x,y)}\le C\bra{\frac{1}{\sqrt{x^2+y^2}}+1}\end{align*}
がすべての$(x,y)\in\R^2\setminus\{(0,0)\}$に対して成り立つとする.
- $f(x+iy):=\dfrac{\partial u}{\partial x}(x,y)-i\dfrac{\partial u}{\partial y}(x,y)$は$\C\setminus\{0\}$上の正則関数となることを示せ.ただし$i$は虚数単位とする.
- 実数$a$, $b$, $c$, $d$が存在して\begin{align*}u(x,y)=a\log{(x^2+y^2)}+bx+cy+d\end{align*}がすべての$(x,y)\in\R^2\setminus\{(0,0)\}$に対して成り立つことを示せ.
2変数の調和関数$u$について,偏導関数$u_x$, $u_y$が$|z|=\sqrt{x^2+y^2}$に関してある程度減衰しているときの$u$の形を求める問題です.
解答の方針とポイント
(1)で誘導されるように,複素解析学(と少しのベクトル解析)を用いて(2)を解きましょう.
正則関数とコーシー・リーマンの方程式
$u$が調和関数である($u_{xx}+u_{yy}=0$を満たす)ことから,$f$の実部$u_x$と虚部$-u_y$がコーシー・リーマンの方程式を満たすので,これで(1)が成り立つことが分かりますね.
領域$D\subset\C$上の関数$f(x+iy)=u(x,y)+iv(x,y)$($x,y\in\R$)に対して,次は同値である.
- $f$は$D$上の正則関数である.
- $u$, $v$はコーシー・リーマンの方程式$u_x=v_y$, $u_y=-v_x$を満たす.
ただし,$u$, $v$は($D\subset\R^2$とみなして)$D$上の2変数実数値関数である.
$u$の最終形から逆算する
目標の形$u(x,y)=a\log{(x^2+y^2)}+bx+cy+d$から
\begin{align*}u_x=\frac{2ax}{x^2+y^2}+b,\quad
u_y=\frac{2ay}{x^2+y^2}+c\end{align*}
となります.逆に,このとき第1式を積分して$u(x,y)=a\log{(x^2+y^2)}+bx+v(y)$であることが分かり,両辺を$y$で微分して$u_y(x,y)=\frac{2ay}{x^2+y^2}+v'(y)$となるので,$v'(y)=c$より$u(x,y)=a\log{(x^2+y^2)}+bx+cy+d$と表せることが分かります.
よって,任意の$(x,y)\in\R^2\setminus\{(0,0)\}$に対して,$f$が
\begin{align*}f(z)&=\bra{\frac{2ax}{x^2+y^2}+b}-i\bra{\frac{2ay}{x^2+y^2}+c}
\\&=\frac{2a\overline{z}}{|z|^2}+b-ic=\frac{2a}{z}+b-ic\quad\dots(*)\end{align*}
の形に表せることを示せばよいですね.
$f$の評価とローラン展開
$f$の実部・虚部の絶対値$|u_x|$, $|u_y|$が原点以外で$C(|z|^{-1}+1)$で上から評価されるので,$|f|$も原点以外で$|z|^{-1}+1$の定数倍で上から評価され,$f$は0を極としても1位であることが分かります.
よって,$f(z)$は0で$\sum\limits_{n=-1}^{\infty}a_nz^n$の形にローラン展開できるので,$f$の目標の形$(*)$と見比べて
- $\sum\limits_{n=0}^{\infty}a_nz^n$が定数
- $a_{-1}\in\R$
であることを示せばよいですね.
リウヴィルの定理から複素関数が定数であることが示せる
複素関数が定数であることを証明する際の常套手段はリウヴィルの定理ですね.
[リウヴィルの定理]複素関数$f$が$\C$全体で正則かつ有界なら定数である.
$f$は$\C\setminus\{0\}$で正則だから,0でのローラン展開から$a_{-1}z^{-1}$を引いた整級数$g(z)=\sum\limits_{n=0}^{\infty}a_nz^n$は$\C$上正則です.
これより,$g$は$|z|\le1$では連続なので有界です.また,$|z|\ge1$では$f$も$\frac{a_{-1}}{z}$も有界なので$g$も有界です.
よって,$g$は$\C$上有界な正則関数だからリウヴィルの定理より$g$は定数関数と分かり,$g(z)=p+qi$, $a_{-1}=r+si$($p,q,r,s$)とおくと
\begin{align*}f(z)=p+qi+\frac{(rx+sy)+(sx-ry)i}{x^2+y^2}\end{align*}
となり,
\begin{align*}\begin{cases}u_x(x,y)=p+\frac{rx+sy}{x^2+y^2},\\
u_y(x,y)=-q-\frac{sx-ry}{x^2+y^2}\end{cases}\end{align*}
が成り立ちますね.
$\nabla{u}$の閉曲線上の線積分
ここから目標の形$(*)$になることを示すには
\begin{align*}a_{-1}\in\R\iff s=0\end{align*}
を示すことになりますね.直観的には$s=0$となることは次のように考えることができます.
もし$s\neq0$なら,$\nabla{u}=\bmat{u_x\\u_y}$の円周$x^2+y^2=r^2$上の接線方向の成分$\bmat{\frac{sy}{x^2+y^2}\\-\frac{sx}{x^2+y^2}}$が$\bmat{0\\0}$でなく一定です.よって,1周すると$u$の流れが増加していることになり,これは$u$が1価関数であることに矛盾しますね.
そこで,このことを厳密に示すには,閉曲線上の変化の総和が0になることを意味する次の線積分の定理を使えばよいですね.
領域$D\subset\R^n$上の$C^1$級関数$\phi$を考える.$D$上の任意の区分的$C^1$級閉曲線$C$に対して,
\begin{align*}\int_{C}\nabla{\phi}(\m{x})\cdot d\m{x}=0\end{align*}
が成り立つ.
解答例
(1)の解答
$u$は$C^2$級なので,$u_{xy}=u_{yx}$が成り立つことに注意する.領域$\R^2\setminus\{(0,0)\}$上で
\begin{align*}&(u_x)_x=u_{xx}=-u_{yy}=(-u_y)_y,
\\&(u_x)_y=u_{xy}=u_{yx}=-(-u_y)_x\end{align*}
だから,$f$の実部$u_x$と虚部$-u_y$はコーシー・リーマンの方程式を満たす.よって,$f$は$\C\setminus\{0\}$上で正則である.
(2)の解答
(1)の$f$を用いる.任意の$z=x+iy\in\C\setminus\{0\}$($x,y\in\R$)に対して,
\begin{align*}|f(z)|&=\sqrt{|u_x(x,y)|^2+|u_y(x,y)|^2}\le|u_x(x,y)|+|u_y(x,y)|
\\&\le C\bra{\frac{1}{\sqrt{x^2+y^2}}+1}=C\bra{\frac{1}{|z|}+1}\end{align*}
だから,$|zf(z)|\le C(1+|z|)$が成り立つ.これより$zf(z)$は0の除外近傍上で有界だから,0は$zf(z)$の除去可能な特異点と分かり,$f(z)=\sum\limits_{n=-1}^{\infty}a_nz^n$とローラン展開できる.
$f$は$\C\setminus\{0\}$上正則だから,$g(z)=\sum\limits_{n=0}^{\infty}a_nz^n$で定まる複素関数$g$は$\C$上で正則である.また,$g$は連続(正則)だから有界閉集合$\set{z\in\C}{|z|\le1}$上で有界であり,$\set{z\in\C}{|z|\ge1}$上で
\begin{align*}|g(z)|&=\abs{f(z)-\frac{a_{-1}}{z}}\le|f(z)|+\frac{|a_{-1}|}{|z|}
\\&\le C\bra{\frac{1}{|z|}+1}+\frac{|a_{-1}|}{|z|}\le2C+|a_{-1}|\end{align*}
となって有界だから,$g$は$\C$全体で有界である.よって,リウヴィルの定理より$g$は定数関数なので,
\begin{align*}f(z)=g(z)+\frac{a_{-1}}{z}=b-ci+\frac{(2ax+ky)+(kx-2ay)i}{x^2+y^2}\end{align*}
と表せる.ただし,$g(z)=b-ci$, $a_{-1}=2a+ki$とおいた($a,b,c,k\in\R$).これより
\begin{align*}\begin{cases}u_x(x,y)=b+\frac{2ax+ky}{x^2+y^2},\\
u_y(x,y)=c-\frac{kx-2ay}{x^2+y^2}\end{cases}\end{align*}
が成り立つ.
$u$は$C^2$級だから$\int_{|z|=1}\nabla{u}(x,y)\cdot\sbmat{dx\\dy}=0$であり,
\begin{align*}&\int_{|z|=1}\nabla{u}(x,y)\cdot\bmat{dx\\dy}=\int_{|z|=1}(u_x(x,y)\,dx+u_y(x,y)\,dy)
\\&=\int_{0}^{2\pi}\{(b+2a\cos{\theta}+k\sin{\theta})(-\sin{\theta})-(-c+k\cos{\theta}-2a\sin{\theta})\cos{\theta}\}\,d\theta
\\&=-\int_{0}^{2\pi}(k+b\sin{\theta}-c\cos{\theta})\,d\theta=-2k\pi\end{align*}
だから$k=0$が成り立つ.よって,
\begin{align*}\begin{cases}u_x(x,y)=b+\frac{2ax}{x^2+y^2},\\
u_y(x,y)=c+\frac{2ay}{x^2+y^2}\end{cases}\end{align*}
が成り立つ.第1式より
\begin{align*}u(x,y)=bx+a\log{(x^2+y^2)}+v(y)\end{align*}
と表せる($v$は任意関数).$u$は$C^2$級だから$v$も$C^2$級なので,$u$を$y$で偏微分して
\begin{align*}u_y(x,y)=\frac{2ay}{x^2+y^2}+v'(y)\end{align*}
となるから,$u_y(x,y)=c+\frac{2ay}{x^2+y^2}$と比較して$v'(y)=c$が成り立ち,$v(y)=cy+d$を得る($d$は任意定数).
以上より,任意の$(x,y)\in\R^2\setminus\{(0,0)\}$に対して,$u(x,y)=a\log{(x^2+y^2)}+bx+cy+d$が成り立つ.
第6問(微分幾何学)
$n$を正の整数,$a$を実数とし,$\R^3$の部分集合$X$を
\begin{align*}X=\set{(x,y,z)\in\R^3}{x^2+y^4+az^n=1}\end{align*}
で定める.
- $X$は$\R^3$の微分可能部分多様体であることを示せ.
- 関数$f:X\to\R$を$f(x,y,z)=z$で定める.$f$がちょうど2個の臨界点を持つような$n$, $a$をすべて求めよ.
$X$上の関数$f$がちょうど2個の臨界点(停留点)を持つための条件を求める問題です.
解答の方針とポイント
(1)は正則値定理(沈め込み定理)を用いるのが常套手段です.(2)は$p$が臨界点であることを接空間$T_pX$の条件に書き換えて初等的な議論(線形代数)に持ち込みます.
正則値定理で可微分多様体であることを示す
部分多様体であることの証明には,次の正則値定理(沈め込み定理)を使うのが常套手段です.
[正則値定理(沈め込み定理)]$C^s$級微分可能多様体$M$, $N$と,$C^s$級写像$f:M\to N$に対して,$f$の正則値$q\in N$の逆像$f^{-1}(q)$は$M$の$(\dim{M}-\dim{N})$次元$C^s$級部分多様体である.
本問(1)では$g:\R^3\to\R$を$g(x,y,z)=x^2+y^4+az^n-1$で定めると$g^{-1}(0)=X$なので,あとは0が$g$の正則値であることを示せばよいですね.
微分可能多様体$M$, $N$に対して,$C^1$級写像$f:M\to N$を考える.$a\in N$が$f$の正則値であるとは,$f^{-1}(a)$に属する任意の点が正則点である(臨界点でない)ことをいう.
多様体上の写像の臨界点
$f:X\to\R$の変化が止まる点$p\in X$が$f$の臨界点です.言い換えれば,$f$の$\R^3$への自然な延長$F:\R^3\to\R;(x,y,z)\mapsto z$について,点$(x,y,z)$を$X$上で動かして,$f$の変化が止まる点$p\in X$が$f$の臨界点です.
したがって,$f$の微分$df_p:T_{p}X\to\R$の定義域$T_{p}X$が$dF_p:\R^3\to\R$の核に含まれているような点$p\in X$が臨界点なので,
\begin{align*}\operatorname{Ker}dg_p=T_{p}X\subset\operatorname{Ker}dF_{p}\end{align*}
を満たす$p\in X$がちょうど2個であるような$n$, $a$を求めれば良いですね.
この論法は$f$の値域が1次元多様体であることから成り立ちます.$f$の値域の多様体$N$が2次元以上の場合は,$p\in M$が臨界点であることが$\rank{df_p}<\dim{N}$と定義されるので,$T_p M\subset\operatorname{Ker}dF_p$からは解けません.
解答例
(1)の解答
$C^\infty$級写像$g:\R^3\to\R$を
\begin{align*}g(x,y,z)=x^2+y^4+az^n-1\end{align*}
で定める.$X=g^{-1}(0)$であり,$(1,0,0)\in X$だから$X\neq\emptyset$である.
任意の$p=(x,y,z)\in\R^3$に対して$Jg_p=[2x,4y^3,anz^{n-1}]$だから,
\begin{align*}\rank{Jg_{p}}=0
\iff x=0\ \text{かつ}\ y=0\ \text{かつ}\ az^{n-1}=0\end{align*}
である.よって,もし$p=(x,y,z)\in X$が$\rank{Jg_{p}}=0$を満たすなら,$az^{n-1}=0$かつ$az^n=1$が成り立つことになるが,これらは矛盾する.
したがって,任意の$p\in X$に対して$\rank{Jg_{p}}=1$だから$p$は正則点である.$p$の任意性より0は$g$の正則値だから,正則値定理より$X=g^{-1}(0)$は$C^\infty$級微分可能多様体である.
(2)の解答
$f:X\to\R$の$\R^3$への延長$F:\R^3\to\R$を$F(x,y,z)=z$で定める.
このとき,$p=(x,y,z)\in X$が$f$の臨界点であることと,$T_pX\subset\operatorname{Ker}dF_p$が成り立つことは同値である.
さらに,$X\subset\R^3$より$T_pX\subset\R^3$とみなすことができ,$JF_p=[0,0,1]$より$\operatorname{Ker}dF_p=\R^2\times\{0\}$なので,$T_pX\subset\R^2\times\{0\}$となる$p\in X$がちょうど2個である$n$, $a$を全て求めればよい.ここで,
\begin{align*}T_pX&=\operatorname{Ker}dg_p
=\set{\bmat{s\\t\\u}\in\R^3}{Jg_p\bmat{s\\t\\u}=0}
\\&=\set{\bmat{s\\t\\u}\in\R^3}{2xs+4y^3t+anz^{n-1}u=0}\end{align*}
である.
$p\in X$が$(x,y)\neq(0,0)$を満たすなら,$2xs+4y^3t+anz^{n-1}u=0$かつ$u\neq0$を満たす$(s,t,u)$が存在し$T_pX\subset\R^2\times\{0\}$とはならない.よって,$T_pX\subset\R^2\times\{0\}$となる$p\in X$は$p=(0,0,k)$($k\in\R$)の形に限り,さらに$p\in X$であることより$k$は$ak^n=1$を満たす.
したがって,$T_pX\subset\R^2\times\{0\}$となる$p\in X$が2個存在するなら,$ak^n=1$を満たす$k$が2個存在するので,$a>0$かつ$n$が正の偶数であることが必要である.
逆に,$a>0$かつ$n$が正の偶数であれば,$T_pX\subset\R^2\times\{0\}$となる$p\in X$は$p=(0,0,\pm a^{-1/n})$のちょうど2個存在する.
以上より,$f$がちょうど2個の臨界点を持つような$n$, $a$は,$a>0$かつ$n$が偶数であるような$n$, $a$で全部である.
第7問(集合論)
整数$n\ge2$に対して,$E_n=\{1,2,\dots,n\}$とおく.$E_n$の濃度2の部分集合全体を$\binom{E_n}{2}$と表し,また$\binom{E_n}{2}$の濃度$n-1$の部分集合$S$のうち,以下の条件$(*)$を満たすもの全体を$E_n^*$と表す.
$(*)$ 任意の$T,T’\in S$について,$T\cap T’\neq\emptyset$.
さらに写像$F_n:E_n\to E_n^*$を
\begin{align*}F_n(i)=\set{T\in\binom{E_n}{2}}{i\in T}\end{align*}
で定める.このとき,$F_n$が全単射となるような整数$n\ge2$をすべて求めよ.
集合$E_n$と集合系の集合$E_n^*$が全単射で対応するための次元の条件を求める問題です.
解答の方針とポイント
具体的な$n$できちんと実験して観察すればそう難しくない問題です.
$n=4$のときの問題の様子
$n=4$のときを考えましょう.$E_4=\{1,2,3,4\}$で,この濃度2の部分集合全体が$\binom{E_4}{2}$なので
\begin{align*}\binom{E_4}{2}=\{\{1,2\},\{1,3\},\{1,4\},\{2,3\},\{2,4\},\{3,4\}\}\end{align*}
です.この$\binom{E_4}{2}$の濃度$3(=4-1)$の部分集合で$(*)$を満たすものは
\begin{align*}&\{\{1,2\},\{1,3\},\{1,4\}\},\quad\{\{1,2\},\{2,3\},\{2,4\}\},\quad\{\{1,3\},\{2,3\},\{3,4\}\},
\\&\{\{1,4\},\{2,4\},\{3,4\}\},\quad\{\{1,2\},\{1,3\},\{2,3\}\},\quad\{\{1,2\},\{1,4\},\{2,4\}\},
\\&\{\{1,3\},\{1,4\},\{3,4\}\},\quad\{\{2,3\},\{2,4\},\{3,4\}\}\end{align*}
の8通りあり,これら全部の集合が$E_4^*$ですね.このとき$|E_4|=4\neq8=|E_4^*|$なので写像$F_4:E_4\to E_4^*$は全単射になりえません.
なお,写像$F_4$は
\begin{align*}&F_4(1)=\{\{1,2\},\{1,3\},\{1,4\}\},\quad
F_4(2)=\{\{1,2\},\{2,3\},\{2,4\}\},
\\&F_4(3)=\{\{1,3\},\{2,3\},\{3,4\}\},\quad
F_4(4)=\{\{1,4\},\{2,4\},\{3,4\}\}\end{align*}
ですね.
$n=5$のときの問題の様子
$n=5$のときを考えましょう.$E_5=\{1,2,3,4,5\}$で,この濃度2の部分集合全体が$\binom{E_5}{2}$なので
\begin{align*}\binom{E_5}{2}=\{&\{1,2\},\{1,3\},\{1,4\},\{1,5\},\{2,3\},\\&\{2,4\},\{2,5\},\{3,4\},\{3,5\},\{4,5\}\}\end{align*}
です.この$\binom{E_5}{2}$の濃度$4(=5-1)$の部分集合で$(*)$を満たすものは
\begin{align*}&\{\{1,2\},\{1,3\},\{1,4\},\{1,5\}\},\quad\{\{1,2\},\{2,3\},\{2,4\},\{2,5\}\},
\\&\{\{1,3\},\{2,3\},\{3,4\},\{3,5\}\},\quad\{\{1,4\},\{2,4\},\{3,4\},\{4,5\}\},
\\&\{\{1,5\},\{2,5\},\{3,5\},\{4,5\}\}\end{align*}
の5通りあり,これら全部の集合が$E_5^*$ですね.このとき$|E_5|=5=|E_5^*|$なので写像$F_5:E_5\to E_5^*$は全単射です.
$n=4$のときは$E_4^*$の元に$\{\{1,2\},\{1,3\},\{2,3\}\}$のような,3つの集合の共通部分が空であるような集合系が存在しました.しかし,$n\ge5$の場合には条件$(*)$を満たす集合系の全ての元(集合)に共通する元が存在しなくてはならず,$|E_n^*|=n$となることが見て取れますね.
以上の考察から,$n<5$の場合は個別に考え,$n\ge5$の場合は一括で議論ができそうですね.
解答例
求める$n$が$n=3$, $n\ge5$であることを示す.
$n=2,3,4$のとき
$\binom{E_2}{2}=\{\{1,2\}\}$だから,$E_2^*=\bigl\{\{\{1,2\}\}\bigr\}$である.$E_2=\{1,2\}$の濃度は2で,$E_2^*$の濃度は1だから,$F_2$は全単射でない.
$\binom{E_3}{2}=\{\{1,2\},\{1,3\},\{2,3\}\}$だから,
\begin{align*}E_3^*=\bigl\{\{\{1,2\},\{1,3\}\},\{\{1,2\},\{2,3\}\},\{\{1,3\},\{2,3\}\}\bigr\}\end{align*}
である.$F_3(1)=\{\{1,2\},\{1,3\}\}$, $F_3(2)=\{\{1,2\},\{2,3\}\}$, $F_3(3)=\{\{1,3\},\{2,3\}\}$なので,$F_3$は全単射である.
$\binom{E_4}{2}=\{\{1,2\},\{1,3\},\{1,4\},\{2,3\},\{2,4\},\{3,4\}\}$だから,$E_4^*$の元として例えば
\begin{align*}&\{\{1,2\},\{1,3\},\{1,4\}\},\quad\{\{1,2\},\{2,3\},\{2,4\}\},\quad\{\{1,3\},\{2,3\},\{3,4\}\},
\\&\{\{1,4\},\{2,4\},\{3,4\}\},\quad\{\{1,2\},\{1,3\},\{2,3\}\}\end{align*}
が挙げられ,$E_4^*$の濃度は5以上である.一方,$E_4=\{1,2,3,4\}$の濃度は4だから,$F_4$は全単射でない.
$n\ge5$のとき
$n\ge5$のとき,$F_n$が全単射であることを示す.
任意に$S\in E_n^*$をとる.異なる任意の$A,B,C\in S$をとり,$A\cap B=\{i\}$, $A\cap C=\{j\}$とする.
$i\neq j$と仮定すると,$A=\{i,j\}$であり,ある$k,\ell\in E_n$が存在して,$B=\{k,i\}$, $C=\{j,\ell\}$と表せる.このとき,$A\neq B$より$k\neq j$であり,$A\neq C$より$k\neq i$なので,$B\cap C\neq\emptyset$より$k=\ell$が成り立つ.
よって,異なる$i,j,k\in E_n$により$A=\{i,j\}$, $B=\{i,k\}$, $C=\{j,k\}$と表せることになる.$n\ge5$なので,$A$, $B$, $C$とは異なる$D\in S$が存在するが,$D$は元を2個しかもたないので$A$, $B$, $C$のいずれかとは共通部分が空となるので矛盾する.
したがって,$i=j$が成り立ち,$S$のどの元(集合)もある$i\in E_n$をもつ.また,$i\in E_n$を元にもつ$\binom{E_n}{2}$の元(集合)は$n-1$個しかないので,
\begin{align*}S_i=\{\{i,1\},\dots,\{i,i-1\},\{i,i+1\},\dots,\{i,n\}\}\end{align*}
とおくと,$E_n^*=\{S_1,S_2,\dots,S_n\}$となる.また,任意の$i\in E_n$に対して,
\begin{align*}F_n(i)=\set{T\in\binom{E_n}{2}}{i\in T}=S_i\end{align*}
だから,$F_n$は全単射である.
参考文献
以下,私も使ったオススメの入試問題集を挙げておきます.
詳解と演習大学院入試問題〈数学〉
[海老原円,太田雅人 共著/数理工学社]
理工系の修士課程への大学院入試問題集ですが,基礎〜標準的な問題が広く大学での数学の基礎が復習できる総合問題集として利用することができます.
実際,まえがきにも「単なる入試問題の解説にとどまらず,それを通じて,数学に関する読者の素養の質を高めることにある」と書かれているように,必ずしも大学院入試を受験しない一般の学習者にとっても学びやすい問題集です.また,構成が読みやすいのも個人的には嬉しいポイントです.
第1章 数え上げと整数
第2章 線形代数
第3章 微積分
第4章 微分方程式
第5章 複素解析
第6章 ベクトル解析
第7章 ラプラス変換
第8章 フーリエ変換
第9章 確率
一方で,問題数はそれほど多くないので,多くの問題を解きたい方には次の問題集もオススメです.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの問題集|詳解と演習 大学院入試問題(数理工学社)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.
演習 大学院入試問題
[姫野俊一,陳啓浩 共著/サイエンス社]
上記の問題集とは対称的に問題数が多く,まえがきに「修士の基礎数学の問題の範囲は,ほぼ本書中に網羅されている」と書かれているように,広い分野から問題が豊富に掲載されています.
全2巻で,
1巻第1編 線形代数
1巻第2編 微分・積分学
1巻第3編 微分方程式
2巻第4編 ラプラス変換,フーリエ変換,特殊関数,変分法
2巻第5編 複素関数論
2巻第6編 確率・統計
が扱われています.
地道にきちんと地に足つけた考え方で解ける問題が多く,確かな「腕力」がつくテキストです.入試では基本問題は確実に解けることが大切なので,その意味で試験への対応力が養われると思います.
なお,私自身は受験生時代に計算力があまり高くなかったので,この本の問題で訓練したのを覚えています.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの問題集|演習 大学院入試問題[数学](サイエンス社)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.




コメント