本質的有界な可測関数｜本質的上限(ess sup)・下限(ess inf)

関数の上限は１点の値を変えることでどこまでも大きくすることができます．例えば，関数$f:\R\to\R$を

$\begin{align*}f(x)=\begin{cases}-x^2+1&(x\neq0),\\2&(x=0)\end{cases}\end{align*}$

で定めると，この関数の値域の上限は$\sup\limits_{x\in\R}{f(x)}=2$ですね．

しかし，この関数は$x=0$での値が飛び跳ねているだけで，$f$の「本質的な上限」は

$\begin{align*}\sup\limits_{x\in\R}(-x^2+1)=1\end{align*}$

と言えそうです．このように考える上限を本質的上限といいます．

この記事では

本質的上限・本質的下限の定義
本質的上限・本質的下限の具体例
本質的上限・本質的下限の性質

を順に説明します．

以下の積分はルベーグ積分として考え，$m$をルベーグ測度としていますが，より一般に測度空間上でも同様に成り立ちます．

「ルベーグ空間$L^p$の基本」の一連の記事

1 本質的上限(ess sup)と本質的下限(ess inf) (今の記事)
2 本質的有界な可測関数のルベーグ空間$L^\infty$
3 ヘルダーの不等式と応用｜測度論の基本不等式
4 ミンコフスキーの不等式｜積分形も合わせて紹介
p乗可積分な可測関数のルベーグ空間Lᵖ（1≦p<∞）(準備中)

本質的上限・本質的下限の定義
1. 本質的上限の定義
2. 本質的下限の定義
本質的上限・本質的下限の具体例
本質的上限・本質的下限の性質

本質的上限・本質的下限の定義

冒頭の例のように，零集合上で値が「跳ねて」いるような部分を無視したときの上界を本質的上界といいます．

通常の上限と同様に，本質的上限は本質的上界の最小のものとして定義されます．

本質的上限の定義

可測集合$A\subset\R$上の可測関数$f$に対して，$S\in\R$が$f$の本質的上界（essential upper bound）であるとは

$\begin{align*}m(\set{x\in A}{f(x)>S})=0\end{align*}$

が成り立つことをいう．$f$の本質的上界が存在するとき，$f$は本質的に上に有界であるという．

言葉で説明すれば，関数$f$の値が$S$より大きくなるような$x$の集合の測度が０であるとき$S$を本質的上界という，ということですね．

例えば，冒頭の関数

$\begin{align*}f(x)=\begin{cases}-x^2+1&(x\neq0),\\2&(x=0)\end{cases}\end{align*}$

を考えると，

$\begin{align*}m\bra{\set{x\in\R}{f(x)>\frac{3}{2}}}=m(\{0\})=0\end{align*}$

なので，$\frac{3}{2}$は$f$の本質的上界のひとつですね．

このような本質的上界全部の集合の下限を本質的上限といいます．

可測集合$A\subset\R$上の本質的に上に有界な可測関数$f$に対して，$f$の本質的上界全部の集合の下限を$f$の本質的上限（essential supremum）といい，$\esssup\limits_{x\in A}{f(x)}$と表す：

$\begin{align*}\esssup_{x\in A}{f(x)}:=\inf\set{S\in\R}{m(\set{x\in A}{f(x)>S})=0}\end{align*}$

ただし，本質的上界が存在しないときは$\esssup\limits_{x\in A}{f(x)}=\infty$と定める．

本質的下限の定義

本質的下限も本質的上限と同様に以下のように定義されます．

可測集合$A\subset\R$上の可測関数$f$に対して，$s\in\R$が$f$の本質的下界（essential under bound）であるとは

$\begin{align*}m(\set{x\in A}{f(x)<s})=0\end{align*}$

が成り立つことをいう．$f$の本質的下界が存在するとき，$f$は本質的に下に有界であるという．

また，$f$の本質的下界の上限を$f$の本質的下限（essential infimum）といい，$\essinf\limits_{x\in A}{f(x)}$と表す：

$\begin{align*}\essinf_{x\in A}{f(x)}:=\sup\set{s\in\R}{m(\set{x\in A}{f(x)<s})=0}\end{align*}$

ただし，本質的上界が存在しないときは$\essinf\limits_{x\in A}{f(x)}=-\infty$と定める．

$f$が本質的に上に有界かつ本質的に下に有界であるとき，$f$は本質的有界であるといいます．

本質的上限・本質的下限の具体例

いくつか具体例を考えましょう．

例１（１点集合を無視する場合）

まずは冒頭の関数の本質的上限・本質的下限を求めましょう．

関数$f:\R\to\R$を

$\begin{align*}f(x)=\begin{cases}-x^2+1&(x\neq0),\\2&(x=0)\end{cases}\end{align*}$

と定める．$f$の本質的上限と本質的下限を求めよ．

この問題の関数$f$は$-x^2+1$とほとんど至る所で等しく，本質的上限は$1$と言えそうですね．

また，本質的下界は存在しそうになく，本質的下限は$-\infty$と言えそうですね．

［本質的上界］一般に一点集合は零集合なので，

$\begin{align*}m(\set{x\in\R}{f(x)>1}) =m(\{0\}) =0\end{align*}$

だから，$1$は$f$の本質的上界である．また，任意の$a<1$に対して

$\begin{align*}&m(\set{x\in\R}{f(x)>a}) \\&=m\Bigl(\bigl(-\sqrt{1-a},\sqrt{1-a}\bigr)\Bigr) \\&=2\sqrt{1-a}>0\end{align*}$

だから，$a$は$f$の本質的上界でない．よって，$\esssup\limits_{x\in\R}{f(x)}=1$を得る．

［本質的下界］任意の$a\in\R$に対して

$\begin{align*}&m(\set{x\in\R}{f(x)<a}) \\&=m\Bigl(\bigl(-\infty,-\sqrt{1-a}\bigr)\cup\bigl(\sqrt{1-a},\infty\bigr)\Bigr) =\infty\end{align*}$

だから，$a$は$f$の本質的下界でない．よって，$\essinf\limits_{x\in\R}{f(x)}=-\infty$を得る．

例２（可算集合を無視する場合）

関数$f:\R\to\R$を

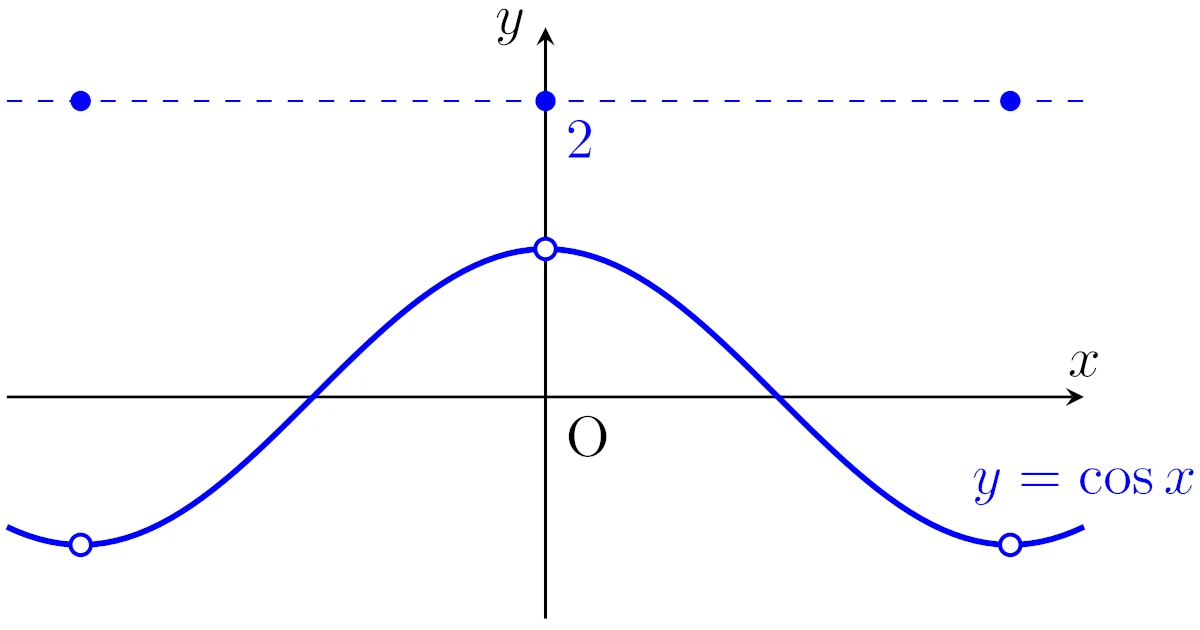
$\begin{align*}f(x)=\begin{cases}\cos{x}&(x\neq0,\pm\pi,\pm2\pi,\dots),\\2&(x=0,\pm\pi,\pm2\pi,\dots)\end{cases}\end{align*}$

と定める．$f$の本質的上限と本質的下限を求めよ．

$x=n\pi$で飛び抜けていますが，一般に可算集合は零集合なので，可算集合$\set{n\pi}{n\in\Z}$はルベーグ測度においては無視されます．

そのため，この問題の関数$f$は$\cos{x}$とほとんど至る所で等しく，本質的上限は１となりそうです．

また，本質的下限は通常の下限と一致して$-1$となりそうです．

［本質的上界］一般に可算集合は零集合なので，

$\begin{align*}m(\set{x\in\R}{f(x)>1}) =m(\set{n\pi}{n\in\Z}) =0\end{align*}$

だから，$1$は$f$の本質的上界である．また，任意の$a\in(0,1)$に対して

$\begin{align*}&\set{x\in\R}{f(x)>a} \\&=\bigcup_{n\in\Z}\bra{-\cos^{-1}{a}+2n\pi,\cos^{-1}{a}+2n\pi}\end{align*}$

なので$m(\set{x\in\R}{f(x)>a})=\infty>0$だから，$a$は$f$の本質的上界でない．よって，$\esssup\limits_{x\in\R}{f(x)}=1$を得る．

［本質的下界］空集合は零集合なので，

$\begin{align*}m(\set{x\in\R}{f(x)<-1}) =m(\emptyset) =0\end{align*}$

だから，$-1$は$f$の本質的上界である．また，任意の$a\in(-1,0)$に対して

$\begin{align*}&\set{x\in\R}{f(x)<a} \\&=\bigcup_{n\in\Z}\bra{-\cos^{-1}{a}+(2n+3)\pi,\cos^{-1}{a}+(2n+1)\pi}\end{align*}$

なので$m(\set{x\in\R}{f(x)<a})=\infty>0$だから，$a$は$f$の本質的下界でない．よって，$\essinf\limits_{x\in\R}{f(x)}=-1$を得る．

例３（可算集合を無視する場合）

関数$f:\R\to\R$を

$\begin{align*}f(x)=\begin{cases}x&(x\in\Q),\\0&(x\in\R\setminus\Q)\end{cases}\end{align*}$

と定める．$f$の本質的上限と本質的下限を求めよ．

有理数全部の集合$\Q$は$\R$上で稠密ですが，$\Q$は可算集合なのでルベーグ測度では無視されます．

よって，この問題の関数$f$は０とほとんど至る所で等しく，本質的下限は０となりそうです．

［本質的上界］一般に可算集合は零集合なので，

$\begin{align*}&m(\set{x\in\R}{f(x)<0})=m(\set{x\in\Q}{x<0})=0\end{align*}$

だから$0$は$f$の本質的上界である．また，任意の$a<0$に対して

$\begin{align*}\set{x\in\R}{f(x)>a}\supset(a,\infty)\end{align*}$

だから，$m$の単調性と併せて

$\begin{align*}&m(\set{x\in\R}{f(x)>a})\ge m((a,\infty))>0\end{align*}$

だから，$a$は$f$の本質的上界でない．よって，$\esssup\limits_{x\in\R}{f(x)}=0$を得る．

［本質的下界］一般に可算集合は零集合なので，

$\begin{align*}m(\set{x\in\R}{f(x)>0})=m(\set{x\in\Q}{x>0})=0\end{align*}$

だから，$0$は$f$の本質的下界でもある．また，任意の$a>0$に対して

$\begin{align*}\set{x\in\R}{f(x)<a}\supset(-\infty,a)\end{align*}$

だから，$m$の単調性と併せて

$\begin{align*}&m(\set{x\in\R}{f(x)<a})\ge m((-\infty,a))>0\end{align*}$

だから，$a$は$f$の本質的下界でない．よって，$\essinf\limits_{x\in\R}{f(x)}=0$を得る．

本質的上限・本質的下限の性質

本質的上限・本質的下限の性質をいくつか紹介します．

本質的上限の最小性・本質的下限の最大性

上の定義では本質的上限$\esssup\limits_{x\in A}{f(x)}$は本質的上界全部の集合の「下限」と定義しましたが，本質的上界全部の集合は必ず最小値をもちます．また，本質的下限についても同様です．

［命題１］可測集合$A\subset\R$上の可測関数$f$が本質的に上に有界なら，本質的上限$\esssup\limits_{x\in A}{f(x)}$は$f$の本質的上界である．また，$f$が本質的に下に有界なら，本質的下限$\essinf\limits_{x\in A}{f(x)}$は$f$の本質的下界である．

正の整数$n$に対して

$\begin{align*}A_n:=\set{x\in A}{f(x)>\esssup\limits_{x\in A}{f(x)}+\frac{1}{n}}\end{align*}$

とおく．$\esssup\limits_{x\in A}{f(x)}+\dfrac{1}{n}$は$f$の本質的上界だから，任意の$n$に対して$m(A_n)=0$である．

さらに，$A_1\subset A_2\subset\dots$なので，測度の単調収束定理より

$\begin{align*}&m\bra{\set{x\in A}{f(x)>\esssup_{x\in A}{f(x)}}} \\&=m\bra{\bigcup_{n=1}^{\infty}A_n} =\lim_{n\to\infty}m(A_n)=0\end{align*}$

が成り立つ．よって，$\esssup\limits_{x\in A}{f(x)}$は$f$の本質的上界である．同様に

$\begin{align*}A'_n:=\set{x\in A}{f(x)<\essinf_{x\in A}{f(x)}-\frac{1}{n}}\end{align*}$

を考えれば，$\essinf\limits_{x\in A}{f(x)}$は本質的下界である．

本質的上限・本質的下限と零集合

本質的上限・本質的下限はうまく零集合を取り除いたときの上限・下限と言えるので以下が成り立ちます．

［命題２］可測集合$A\subset\R$上の可測関数$f$を考える．ある零集合$N\subset A$が存在して，任意の$x\in A\setminus N$に対して

$\begin{align*}\essinf_{x\in A}{f(x)}\le f(x)\le\esssup_{x\in A}{f(x)}\end{align*}$

が成り立つ．

証明には［命題１］を使いましょう．

$\esssup\limits_{x\in A}{f(x)}=\infty$なら右の不等式は常に成り立ち，$\essinf\limits_{x\in A}{f(x)}=\infty$なら左の不等式は常に成り立つから，以下では$f$が本質的有界な場合を示す．

$N_1,N_2\subset A$を

$\begin{align*}&N_1:=\set{x\in A}{f(x)>\esssup_{x\in A}{f(x)}}, \\&N_2:=\set{x\in A}{f(x)<\essinf_{x\in A}{f(x)}}\end{align*}$

とおく．［命題１］より$m(N_1)=m(N_2)=0$が成り立つので，$N:=N_1\cup N_2$とおくと$m$の劣加法性より

$\begin{align*}m(N)\le m(N_1)+m(N_2)=0+0=0\end{align*}$

である．また，$N_1$と$N_2$の定義より，任意の$x\in A\setminus N$に対して

$\begin{align*}\essinf_{x\in A}{f(x)}\le f(x)\le\esssup_{x\in A}{f(x)}\end{align*}$

が従う．

この［命題２］から次の系が従います．

可測集合$A\subset\R$上の可測関数$f$に対して

$\begin{align*}\inf_{x\in A}{f(x)}\le\essinf_{x\in A}{f(x)}\le\esssup_{x\in A}{f(x)}\le\sup_{x\in A}{f(x)}\end{align*}$

が成り立つ．

［命題２］より$\essinf\limits_{x\in A}{f(x)}\le\esssup\limits_{x\in A}{f(x)}$が成り立つ．

上界は本質的上界だから，$\sup{f}$の最小性より$\esssup\limits_{x\in A}{f(x)}\le\sup\limits_{x\in A}{f(x)}$が成り立つ．同様に$\inf\limits_{x\in A}{f(x)}\le\essinf\limits_{x\in A}{f(x)}$が成り立つ．

和の本質的上限・本質的下限

最後に$\esssup$の劣加法性と$\essinf$の優加法性を証明しておきます．

可測集合$A\subset\R$上の可測関数$f$に対して

$\begin{align*}&\esssup_{x\in A}{(f(x)+g(x))}\le\esssup_{x\in A}{f(x)}+\esssup_{x\in A}{g(x)}, \\&\essinf_{x\in A}{(f(x)+g(x))}\ge\essinf_{x\in A}{f(x)}+\essinf_{x\in A}{g(x)}\end{align*}$