ルベーグ空間（Lᵖ空間）｜ルベーグ積分に関するノルム・内積

大雑把に言えば，関数$f$を$p$乗した関数が積分可能であるとき$f$は$p$乗可積分であるといい，$p$乗可積分関数全部の集合を$L^p$と表して，文字通り$L^p$(エルピー) 空間などと呼びます（$1\le p<\infty$）．

詳しく言えば，測度空間$(X,\mathcal{F},\mu)$に対して，

$\begin{align*}\int_{X}|f(x)|^p\,d\mu(x)<\infty\end{align*}$

を満たす$X$上で定義された可測関数$f$全部の集合で，ほとんど至る所等しい関数たちを同一視してできる空間を$L^p(X)$と表します．

$L^p(X)$を扱う大きなメリットのひとつは，ノルムもしくは内積に関して完備性をもつことです．

この記事ではノルム空間となることまで証明し，完備性はのちの記事（準備中）で証明します．

とくに測度空間$(X,\mathcal{F},\mu)$がルベーグ測度空間の部分測度空間であるとき，$L^p(X)$をルベーグ空間と呼びます．

この記事では

可測関数を同一視してできる線形空間
ルベーグ空間$L^p$の定義（$1\le p<\infty$）
補足（複素数値関数の場合の$L^2$内積）

を順に解説します．

「ルベーグ空間$L^p$の基本」の一連の記事

ルベーグ空間（$L^p$空間）の参考文献
可測関数を同一視してできる線形空間
1. 本質的に等しい可測関数の同一視
2. 和とスカラー倍
ルベーグ空間$L^p$の定義（${1\le p<\infty}$）
補足（複素数値関数の場合の$L^2$内積）

ルベーグ空間（$L^p$空間）の参考文献

以下は関数解析に関するオススメの教科書です．

関数解析

ロングセラーの入門書です．基礎から具体例に触れつつ解説されており，初学者にも理解しやすいテキストです．

ルベーグ積分と関数解析

ルベーグ積分から更なるステップに進みたい人向けの教科書です．

可測関数を同一視してできる線形空間

ルベーグ積分においては，ほとんど至る所で等しい関数は積分すると同じ値となるので，同じ関数とみなしたいところです．

そこで，ルベーグ空間$L^p$をきちんと定義するために，ほとんど至る所で等しい関数を同一視する同値関係（商集合）を考える必要があります．

これは本質的有界な関数全部のルベーグ空間$L^\infty$の場合と同様なので，この記事では簡潔な説明に留めることにします．証明など詳しくは以下の記事を参照してください．

本質的有界な関数のルベーグ空間L^∞｜ノルム空間として定義

（適切な同一視のもとで）本質的有界な可測関数全部の集合L^∞はバナッハ空間（完備なノルム空間）となります．この空間L^∞を「ルベーグ空間」と言います．

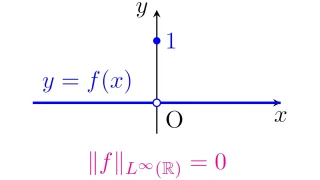
本質的に等しい可測関数の同一視

一般に測度空間$(X,\mathcal{F},\mu)$の零集合（測度０の集合）上でのみ異なっている２つの関数$f$, $g$は$X$上ほとんど至る所で等しいと言うのでした．

$X$上の本質的上限を表す$\|\cdot\|_{L^\infty(X)}$を用いると，２つの関数$f,g:X\to\R$が$X$上ほとんど至る所で等しいことは，$\|f-g\|_{L^\infty(X)}=0$と表すことができますね．

そこで，ほとんど至る所で等しいルベーグ可測関数を同一視してできる空間を考えましょう．

ルベーグ可測集合$X\subset\R^d$上のルベーグ可測関数全部の集合に，関係$\sim$を

$\begin{align*}f\sim g\stackrel{\mathrm{def.}}{\iff}m(\set{x\in X}{f(x)\neq g(x)})=0\end{align*}$

を定めると，関係$\sim$は同値関係となる．ただし，$m$はルベーグ測度である．

つまり，ほとんど至る所で等しい関数たちを同一視する同値関係$\sim$が定まるというわけですね．

「ほとんど至る所」の定義・具体例・応用｜測度空間の零集合

ルベーグ積分では零集合上でのみ例外であることを「ほとんど至る所で」と言います．この記事では「ほとんど至る所で」の定義と具体例を解説したのち，ほとんど至る所で等しい関数の同一視についても解説します．

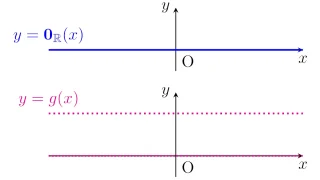
和とスカラー倍

ルベーグ可測集合$X\subset\R^d$上のルベーグ可測関数全部の集合を$L(X)$で表すと，$L(X)$は通常の和・スカラー倍によって線形空間となりますね．

また，$L(X)$を同値関係$\sim$で割ってできる商空間$L(X)/\sim$を$\tilde{L}(X)$で表すことにしましょう．

商空間$\tilde{L}(X)$上の和・スカラー倍を$L(X)$上の和・スカラー倍から自然に定めることにより，$\tilde{L}(X)$も線形空間となります．

ルベーグ可測集合$X\subset\R^d$に対して，$\tilde{L}(X)$上の演算$+$と作用$\cdot$を

$F,G\in\tilde{L}(X)$に対して，代表元$f\in F$, $g\in G$をとり，$L(X)$上の関数の和$f+g$が属する同値類を$F+G$
$F\in\tilde{L}(X)$, $k\in\R$に対して，代表元$f\in F$をとり，$L(X)$上の関数のスカラー倍$kf$が属する同値類を$k\cdot F$

と定めることができ，$+$, $\cdot$それぞれを和・スカラー倍として$\tilde{L}(X)$は実線形空間となる．

$L(X)$上の零ベクトルは「恒等的に値０をとる関数」で，$\tilde{L}(X)$上の零ベクトルは「恒等的に値０をとる関数とほとんど至る所で等しい関数」ですね．

ルベーグ空間$L^p$の定義（${1\le p<\infty}$）

上の準備のもとで，ルベーグ空間$L^p$を定義しましょう．

$p$乗可積分関数の同値類

同値関係$\sim$で割る前の$L(X)$に属するルベーグ可測関数$f$が$p$乗ルベーグ可積分であれば，$f\sim g$となるルベーグ可測関数$g$も$p$乗ルベーグ可積分となります．

$p\in[1,\infty)$とし，可測集合$X\subset\R^d$を考える．$F\in\tilde{L}(X)$のある代表元$f$が$X$上で$p$乗ルベーグ可積分なら，任意の$g\in F$に対して，

$\begin{align*}\int_{X}|f(x)|^p\,dx=\int_{X}|g(x)|^p\,dx<\infty\end{align*}$

が成り立つ．

$\tilde{L}(X)$は商集合なので，$F\in\tilde{L}(X)$は$L(X)$の部分集合であることに注意しましょう．

$f$, $g$は同じ同値類$F$に属するから，$f$, $g$は$X$上ほとんど至る所で等しい．よって，$|f|^p$, $|g|^p$も$X$上ほとんど至る所で等しいから，

$\begin{align*}\int_{X}|f(x)|^p\,dx=\int_{X}|g(x)|^p\,dx\end{align*}$

が成り立つ．$f$は$X$上で$p$乗ルベーグ可積分だから，$\int_{X}|f(x)|^p\,dx<\infty$なので，

$\begin{align*}\int_{X}|g(x)|^p\,dx<\infty\end{align*}$

も成り立つ．

$\tilde{L}(X)$の同値類は関数たちの集合なので本来の関数ではありませんが，いまの命題のように$\tilde{L}(X)$の同じ同値類に属する関数たちの積分は同じ値となるので，一般に$\tilde{L}(X)$の同値類も通常の関数のように扱います．

この記事でも，以下では$p$乗ルベーグ可積分関数が属する同値類$F\in\tilde{L}(X)$を通常の$p$乗ルベーグ可積分関数のように扱います．

ルベーグ空間$L^p$の定義

次の補題の空間$L^p(X)$をルベーグ空間といいます．

$p\in[1,\infty)$とし，ルベーグ可測集合$X\subset\R^d$を考える．$X$上で$p$乗ルベーグ可積分な関数$f\in\tilde{L}(X)$全部の集合$L^p(X)$は，$\tilde{L}(X)$の線形部分空間となる．さらに，

$\begin{align*}\|f\|_{L^p(X)}:=\bra{\int_{X}|f(x)|^p\,dx}^{1/p}<\infty\end{align*}$

で定まる$\|\cdot\|_{L^p(X)}:L^p(X)\to\R$は$L^p(X)$上のノルムである．

$X$上で恒等的に値０をとる関数を$0_{X}$と表す．

$L^p(X)$が部分空間となることの証明

線形部分空間の定義（もしくは必要十分条件）より

$L^p(X)\neq\emptyset$
$L^p(X)$が和で閉じていること
$L^p(X)$がスカラー倍で閉じていること

を示せばよい．

$\int_{X}|0_{X}|^p(x)\,dx=0$だから$0_{X}$は$X$上$p$乗ルベーグ可積分なので，$L^p(X)\neq\emptyset$である．

任意に$f,g\in L^p(X)$と$k\in\R$をとる．$\|f\|_{L^p(X)}<\infty$, $\|g\|_{L^p(X)}<\infty$なので，ミンコフスキーの不等式より

$\begin{align*}\|f+g\|_{L^p(X)}\le\|f\|_{L^p(X)}+\|g\|_{L^p(X)}<\infty\quad\dots(*)\end{align*}$

が従う．また，$\|f\|_{L^p(X)}<\infty$なので，$\|f\|_{L^p(X)}$の定義より

$\begin{align*}\|kf\|_{L^p(X)}&=\bra{\int_{X}|kf(x)|^p\,dx}^{1/p}=\bra{|k|^p\int_{X}|f(x)|^p\,dx}^{1/p} \\&=|k|\bra{\int_{X}|f(x)|^p\,dx}^{1/p}=|k|\|f\|_{L^p(X)}<\infty\quad\dots(**)\end{align*}$

が従う．よって，$L^p(X)$が$\tilde{L}(X)$の和・スカラー倍により閉じているから，$L^p(X)$は$\tilde{L}(X)$の線形部分空間である．

$\|\cdot\|_{L^p(X)}$がノルムとなることの証明

劣加法性はミンコフスキーの不等式$(**)$そのものであり，斉次性は$(*)$により示されている．よって，あとは残る非退化性を示せばよい．

$L^p(X)$上の零ベクトルは$0_{X}$（とほとんど至る所で等しい関数の同値類）であり，

$\begin{align*}\|0_{X}\|_{L^p(X)}=\bra{\int_{X}|0_{X}|^p\,dx}^{1/p}=0^{1/p}=0\end{align*}$

が成り立つ．

逆に$f$が$L^p(X)$上の零ベクトルでないとすると，

$\begin{align*}B:=\set{x\in X}{f(x)\neq0}\end{align*}$

は$m(B)>0$を満たす（$f$はルベーグ可測関数だから$B$はルベーグ可測集合であることに注意）．また

$\begin{align*}B_n:=\set{x\in X}{|f(x)|\ge\frac{1}{n}}\quad(n=1,2,\dots)\end{align*}$

とすると$B=\bigcup_{n=1}^{\infty} B_n$である．$B_n\subset B_{n+1}$と併せて

$\begin{align*}\lim_{n\to\infty}m(B_n)=m(B)\end{align*}$

が成り立つ．よって，ある$N\in\N$が存在して$m(B_N)>\frac{1}{2}m(B)>0$となるから，

$\begin{align*}\|f\|_p&\ge\bra{\int_{B_N}|f(x)|^p\,dx}^{1/p}\ge\bra{\int_{B_N}\frac{1}{N^p}\,dx}^{1/p} \\&=\bra{\frac{1}{N^p}m(B_N)}^{1/p}=\frac{1}{N}m(B_N)^{1/p}>0\end{align*}$

となって，$\|f\|_p\neq0$が従う．

ノルム$\|f\|_{L^p(X)}$の定義で全体を1/p乗しているのは，斉次性$\|kf\|_p=|k|\|f\|_p$が成り立つようにするためですね．

これでノルム空間としてのルベーグ空間$L^p(X)$が次のように定義できることが分かりました．

$p\in[1,\infty)$とし，ルベーグ可測集合$X\subset\R^d$を考える．$\tilde{L}(X)$の$p$乗ルベーグ可積分関数全部の部分空間

$\begin{align*}&\set{f\in\tilde{L}(X)}{\|f\|_{L^p(X)}<\infty}, \\&\|f\|_{L^p(X)}:=\bra{\int_{X}|f(x)|^p\,dx}^{1/p}\end{align*}$

のノルム$\|\cdot\|_{L^p(X)}$を備えたノルム空間をルベーグ空間（Lebesgue space）といい，$L^p(X)$と表す．

このノルム$\|\cdot\|_{L^p(X)}$を$L^p$ノルムといいます．$L^p$ノルムはもとから$1/p$乗されているので，$p$乗すれば

$\begin{align*}\|f\|_{L^p(X)}^p=\int_{X}|f(x)|^p\,dx\end{align*}$

となることは当たり前にしておきましょう．

内積空間としての$L^2$

実は$p=2$の場合のルベーグ空間$L^p$は自然に内積空間となります．

このことを示すために，次の線形代数学の一般論を確認しておきましょう．

実ノルム空間$(V,\|\cdot\|)$に対して，次は同値である．

任意の$\m{u},\m{v}\in V$に対して
$\begin{align*}\|\m{u}+\m{v}\|^2+\|\m{u}-\m{v}\|^2=2(\|\m{u}\|^2+\|\m{v}\|^2)\end{align*}$

が成り立つ．
$(\cdot,\cdot):V\times V\to\R$を
$\begin{align*}(\m{u},\m{v})=\frac{1}{4}(\|\m{u}+\m{v}\|^2-\|\m{u}-\m{v}\|^2)\end{align*}$

で定めると，$(\cdot,\cdot)$が$V$上の内積となる．

さらに，これらのいずれか一方（したがって両方）を満たすとき，任意の$\m{u}\in V$に対して$(\m{u},\m{u})=\|\m{u}\|^2$が成り立つ．

(1)の等式を中線定理ということから，この補題は標語的に「ノルム空間が内積空間となるための必要十分条件は，中線定理が成り立つことである」と言いますね．

この補題を用いると，上で定めた$L^2$ノルムにより，$L^2$の内積が自然に定まることが分かります．

ルベーグ可測集合$X\subset\R^d$に対して，ルベーグ空間$L^2(X)$は

$\begin{align*}(f,g)=\int_{X}f(x)g(x)\,dx\end{align*}$

で定まる内積$(\cdot,\cdot):L^2(X)\times L^2(X)\to\R$により内積空間となり，このときのノルムは$L^2$ノルム$\|\cdot\|_{L^2(X)}$である．

任意の$f,g\in L^2(X)$に対して，

$\begin{align*}&\|f+g\|_{L^2(X)}^2+\|f-g\|_{L^2(X)}^2 \\&=\int_{X}|f(x)+g(x)|^2\,dx+\int_{X}|f(x)-g(x)|^2\,dx \\&=2\int_{X}(f(x)^2+g(x)^2)\,dx \\&=2\bra{\int_{X}|f(x)|^2\,dx+\int_{X}|g(x)|^2\,dx} \\&=2(\|f\|_{L^2(X)}^2+\|g\|_{L^2(X)}^2)\end{align*}$

が成り立つから，補題より$L^2(X)$は

$\begin{align*}(f,g)&=\frac{1}{4}(\|f+g\|_{L^2(X)}^2-\|f-g\|_{L^2(X)}^2) \\&=\frac{1}{4}\bra{\int_{X}|f(x)+g(x)|^2\,dx-\int_{X}|f(x)-g(x)|^2\,dx} \\&=\int_{X}f(x)g(x)\,dx\,dx\end{align*}$

で定まる$(\cdot,\cdot):L^2(X)\times L^2(X)\to\R$を内積として内積空間となる．

この内積を$L^2$内積といいます．

補足（複素数値関数の場合の$L^2$内積）

以上は関数が実数値の場合で，複素数値の場合もほとんど並行してルベーグ空間$L^p$が定義され，ノルムの形は実数値の場合と同じです．

しかし，$L^2$内積について少し事情が変わります．これは線形代数学の一般論として挙げた補題が，複素ノルム空間の場合に次のように変わることに起因します．

複素ノルム空間$(V,\|\cdot\|)$に対して，次は同値である．

任意の$\m{u},\m{v}\in V$に対して
$\begin{align*}\|\m{u}+\m{v}\|^2+\|\m{u}-\m{v}\|^2=2(\|\m{u}\|^2+\|\m{v}\|^2)\end{align*}$

が成り立つ．
$(\cdot,\cdot):V\times V\to\R$を
$\begin{align*}(\m{u},\m{v})=\frac{1}{4}(\|\m{u}+\m{v}\|^2-\|\m{u}-\m{v}\|^2+i\|\m{u}+i\m{v}\|^2-i\|\m{u}-i\m{v}\|^2)\end{align*}$

で定めると，$(\cdot,\cdot)$が$V$上の内積となる．