 微分積分学の基本
微分積分学の基本 有理数の稠密性|実数の「アルキメデスの性質」から証明する
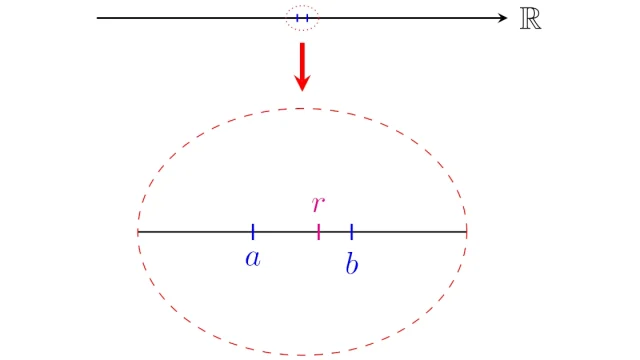
有理数が実数(数直線)上に密に存在しているという性質を「有理数の集合の稠密性」といいます.この証明には「アルキメデスの性質」と呼ばれる実数の重要性質を用います.
 微分積分学の基本
微分積分学の基本  微分積分学の基本
微分積分学の基本  その他
その他  微分積分学の基本
微分積分学の基本 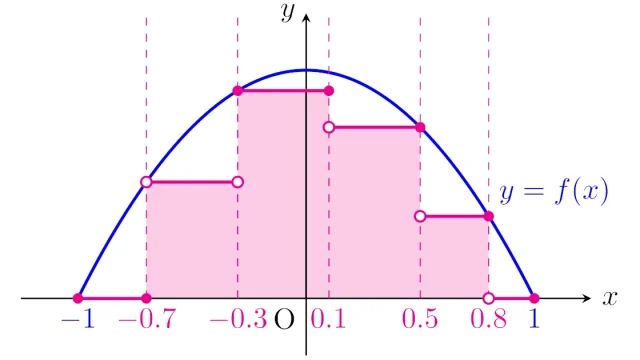 ルベーグ積分の基本
ルベーグ積分の基本 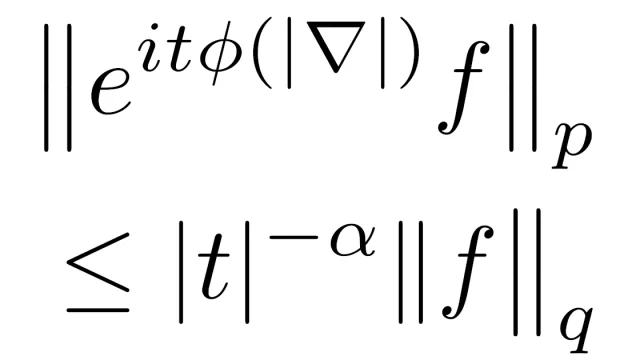 偏微分方程式
偏微分方程式 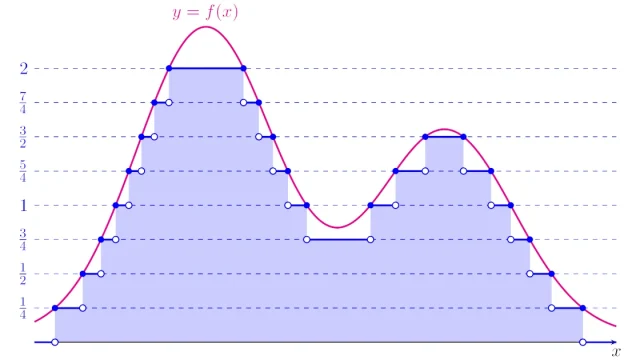 ルベーグ積分の基本
ルベーグ積分の基本  微分積分学
微分積分学 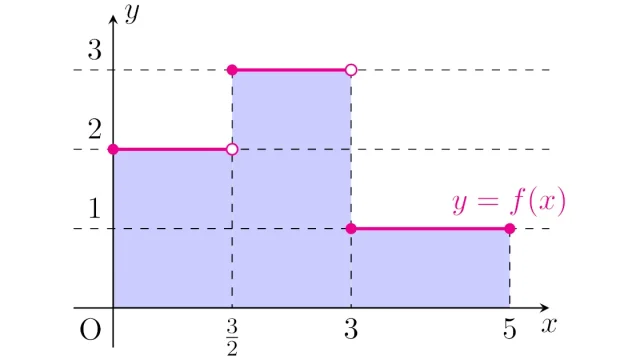 ルベーグ積分の基本
ルベーグ積分の基本  微分積分学
微分積分学