単関数列の項別積分定理｜考え方と応用と証明を解説

微分積分学で学ぶリーマン積分では，有界閉区間$[a,b]$上で定義された可積分関数列$\{f_n\}$が可積分関数に一様収束するとき，

$\begin{align*}\lim_{n\to\infty}\int_{a}^{b}f_n(x)\,dx=\int_{a}^{b}\lim_{n\to\infty}f_n(x)\,dx\end{align*}$

と極限と積分の順序交換ができるのでした．

このように，極限と積分の順序交換ができるような関数列$\{f_n\}$は項別積分可能であるといいます．

ルベーグ積分に関する項別積分定理のベースとなる定理として，適当な単関数列$\{f_n\}$が項別積分可能であるという定理があります．

この記事では，

単関数列の項別積分定理
証明に必要な命題
単関数列の項別積分定理の証明

を順に説明します．

以下ではルベーグ測度を$m$で表します．また，ルベーグ可測集合のことを単に「可測集合」と呼び，ルベーグ可測関数のことを単に「可測関数」と呼びます．

「ルベーグ積分の基本」の一連の記事

ルベーグ積分入門
1. 0 ルベーグ積分の基礎｜リーマン積分の先へ！積分の歴史から紹介

ルベーグ測度

ルベーグ可測関数とルベーグ積分

ルベーグ積分の性質と項別積分

ルベーグ積分の参考文献
1. ルベグ積分入門
2. ルベーグ積分と関数解析
単関数列の項別積分定理
1. 単関数近似定理（復習）
2. 単関数列の項別積分定理
単関数列の項別積分定理の応用（線形性の証明）
単関数列の項別積分定理の証明

ルベーグ積分の参考文献

以下はルベーグ積分に関するオススメの教科書です．

ルベグ積分入門

ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．

ルベーグ積分と関数解析

ルベーグ積分から更なるステップに進みたい人向けの教科書です．

単関数列の項別積分定理

単関数列の項別積分定理が成り立つイメージをもつために，非負値可測関数の単関数近似定理を確認してから，単関数列の項別積分定理を紹介します．

単関数近似定理（復習）

次の定理を（非負値可測関数の）単関数近似定理というのでした．

[単関数近似定理] 可測集合$A$上の非負値可測関数$f$に対して，ある非負値可測単関数列$\{f_n\}$が存在して，

$\begin{align*}f_1\le f_2\le\dots,\quad \lim_{n\to\infty}f_n=f\end{align*}$

が成り立つ．

つまり，非負値可測関数を下から近似する増加単関数列が存在するということですね．

単関数列の項別積分定理

単関数近似定理で非負値可測関数$f$を近似する可測単関数列$\{f_n\}$を考えると，$n$を大きくすると$\dint_{A}f_n(x)\,dx$が$\dint_{A}f(x)\,dx$に近付いていきそうですね．

実際これは正しく，次のように述べることができます．

[単関数列の項別積分定理] 可測集合$A$上の非負値可測関数$f$と，条件

$\begin{align*}f_1\le f_2\le\dots,\quad \lim_{n\to\infty}f_n=f\end{align*}$

を満たす非負値可測単関数列$\{f_n\}$に対して，

$\begin{align*}\lim_{n\to\infty}\int_{A}f_n(x)\,dx=\int_{A}\lim\limits_{n\to\infty}f_n(x)\,dx=\int_{A}f(x)\,dx\end{align*}$

が成り立つ．すなわち，$\{f_n\}$は項別積分可能である．

$\lim\limits_{n\to\infty}f_n=f$なので，$\dint_{A}\lim\limits_{n\to\infty}f_n(x)\,dx=\dint_{A}f(x)\,dx$が成り立つことは当たり前ですね．

この定理を単関数列の項別積分定理と呼びます．

単関数列の項別積分定理の応用（線形性の証明）

単関数列の項別積分定理を証明する前に，重要な応用をひとつ紹介します．

可測集合$A$上の非負値可測関数$f,g$と定数$s,t\in\R$に対して，

$\begin{align*}\int_{A}(sf+tg)(x)\,dx=s\int_{A}f(x)\,dx+t\int_{A}g(x)\,dx\end{align*}$

が成り立つ．

２つのステップに分けて証明しましょう．ステップ１では単関数に対して示し，ステップ２で一般の場合に対して示します．

以下では集合$X\subset A$に対して$I_X$は定義関数を表す：

$\begin{align*}I_X(x)=\begin{cases}1,&x\in X,\\0,&x\in A\setminus X.\end{cases}\end{align*}$

[ステップ１] $f,g$が単関数の場合に成り立つことを示す．

$\begin{align*}f=\sum_{k=1}^{n}\alpha_k I_{A_k},\quad g=\sum_{\ell=1}^{m}\beta_\ell I_{B_\ell}\end{align*}$

とする．ただし，集合$A_1,\dots,A_n,B_1,\dots,B_m$は可測集合で

$A=A_1\cup\dots\cup A_n$, $B=B_1\cup\dots\cup B_m$
$A_i\cap A_j=\emptyset$ ($i\neq j$), $A_p\cap A_q=\emptyset$ ($p\neq q$)

を満たすとする．このとき，

$\begin{align*}&sf+tg=s\sum_{k=1}^{n}\alpha_k I_{A_k}+t\sum_{\ell=1}^{m}\beta_\ell I_{B_\ell} \\&=s\sum_{k=1}^{n}\alpha_k \sum_{\ell=1}^{m}I_{A_k\cap B_\ell}+t\sum_{\ell=1}^{m}\beta_\ell \sum_{k=1}^{n}I_{A_k\cap B_\ell} \\&=\sum_{k=1}^{n}\sum_{\ell=1}^{m}(s\alpha_k+t\beta_\ell)I_{A_k\cap B_\ell}\end{align*}$

である．いま$A_k\cap B_\ell$ ($k=1,\dots,n$, $\ell=1,\dots,m$)は可測集合であり，$A$を互いに素に分割するから単関数のルベーグ積分より

$\begin{align*}&\int_{A}(sf+tg)(x)\,dx =\sum_{k=1}^{n}\sum_{\ell=1}^{m}(s\alpha_k+t\beta_\ell)m(A_k\cap B_\ell) \\&=s\sum_{k=1}^{n}\sum_{\ell=1}^{m}\alpha_k m(A_k\cap B_\ell)+t\sum_{k=1}^{n}\sum_{\ell=1}^{m}\beta_\ell m(A_k\cap B_\ell) \\&=s\sum_{k=1}^{n}\alpha_k m(A_k)+t\sum_{\ell=1}^{m}\beta_\ell m(B_\ell) \\&=s\int_{A}f(x)\,dx+t\int_{A}g(x)\,dx\end{align*}$

が成り立つ．

[ステップ２] $f,g$が一般の場合に成り立つことを示す．

単関数近似定理より，ある非負値可測単関数列$\{f_n\},\{g_n\}$が存在して，

$\begin{align*}&f_1\le f_2\le\dots,\quad \lim_{n\to\infty}f_n=f, \\&g_1\le g_2\le\dots,\quad \lim_{n\to\infty}g_n=g\end{align*}$

が成り立つ．ステップ１より単関数$f_n,g_n$に対しては

$\begin{align*}\int_{A}(sf_n+tg_n)(x)\,dx=s\int_{A}f_n(x)\,dx+t\int_{A}g_n(x)\,dx\end{align*}$

が成り立つから，両辺で$n\to\infty$をとれば単関数列の項別積分定理より

$\begin{align*}\int_{A}(sf+tg)(x)\,dx=s\int_{A}f(x)\,dx+t\int_{A}g(x)\,dx\end{align*}$

が従う．

ステップ１の単関数の場合を踏まえて，ステップ２では

単関数近似定理
単関数列の項別積分定理

を組み合わせることで示したわけですね．

このように解析学では「簡単な場合に証明したのち，極限をとってより一般の場合を示す」という証明方法がよく用いられます．

一般の可測関数のルベーグ積分は正成分と負成分に分けて定義されたことから，一般の可測関数のルベーグ積分でも線形性をもちます．

単関数列の項別積分定理の証明

証明に必要な補題・命題を用意し，単関数列の項別積分定理を証明しましょう．

補題

[補題] $m(A)<\infty$なる可測集合$A$上の非負値可測関数$f$と，恒等的に値$\lambda>0$をとる関数$\Lambda$を考える．任意の$x\in A$に対して$f(x)\ge\lambda$が成り立つとすると，

$\begin{align*}\int_{A}(f-\Lambda)(x)\,dx=\int_{A}f(x)\,dx-\lambda m(A)\end{align*}$

が成り立つ．

一般に連続関数は可測関数なので$\Lambda$は可測関数だから，$f$が可測関数であることと併せて$f-\Lambda$も可測関数であることに注意する．

$A$を

$A=A_1\cup\dots\cup A_n$
$A_i\cap A_j=\emptyset$ ($i\neq j$)

を満たす任意の可測集合$A_1,\dots,A_n$で分割し，$\alpha_k:=\inf\limits_{x\in A_k}f(x)$とおく．このとき，

$\begin{align*}\sum_{k=1}^{n}(\alpha_k-\lambda)m(A_k)=\sum_{k=1}^{n}\alpha_k m(A_k)-\lambda m(A)\end{align*}$

が成り立ち，左辺は$f-\Lambda$の$A$上の近似和，右辺の第１項は$f$の$A$上の近似和である．

よって，両辺で$A$のあらゆる可測集合による分割$A_1,\dots,A_n$を考えたときの上限をとると

$\begin{align*}\int_{A}(f-\Lambda)(x)\,dx=\int_{A}f(x)\,dx-\lambda m(A)\end{align*}$

が従う．

測度の単調収束

次の命題は一般の測度空間でも成り立ち，測度の単調収束定理と呼ばれることもあります．

可測集合$A_1,A_2,\dots$に対して，次が成り立つ．

$A_1\subset A_2\subset\dots$なら$m{\bra{\bigcup\limits_{n=1}^{\infty}A_n}}=\lim\limits_{n\to\infty}m(A_n)$
$A_1\supset A_2\supset\dots$かつある$N\in\N$が存在して$m(A_N)<\infty$なら$m{\bra{\bigcap\limits_{n=1}^{\infty}A_n}}=\lim\limits_{n\to\infty}m(A_n)$

それぞれざっくり言えば

集合がどんどん大きくなるなら，全ての集合の和集合の測度は測度の極限に一致する
集合がどんどん小さくなり，途中から有限測度になるなら，全ての集合の共通集合の測度は測度の極限に一致する

ということですね．

単関数列の項別積分定理では(1)のみ用います．

測度の単調収束定理の証明は以下の記事を参照してください．

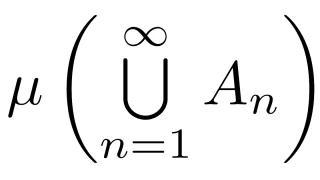
測度の単調収束定理とその応用｜集合の単調増大列・単調減少列の測度

測度論において可測集合の列{Aₙ}に対して，Aₙの測度の極限を考えることはよくあります．この記事では，測度の極限に関する「測度の単調収束定理」の証明と補足をします．

単関数列の項別積分定理の証明

[単関数列の項別積分定理（再掲）] 可測集合$A$上の非負値可測関数$f$と，条件

$\begin{align*}f_1\le f_2\le\dots,\quad \lim_{n\to\infty}f_n=f\end{align*}$

を満たす非負値可測単関数列$\{f_n\}$に対して，

$\begin{align*}\lim_{n\to\infty}\int_{A}f_n(x)\,dx=\int_{A}f(x)\,dx\end{align*}$

が成り立つ．すなわち，$\{f_n\}$は項別積分可能である．

仮定より任意の$n$に対して$f_n\le f$なので，上で示した補題から

$\begin{align*}\int_{A}f_n(x)\,dx\le\int_{A}f(x)\,dx\end{align*}$

が成り立つ．また，左辺は$n$に関して単調増加である．よって，左辺は$n\to\infty$で収束して

$\begin{align*}\lim_{n\to\infty}\int_{A}f_n(x)\,dx\le\int_{A}f(x)\,dx\end{align*}$

が成り立つ．よって，あとは$\ge$の向きの不等式を示せばよい．

[場合１] ある$c>0$が存在して，$m(\set{x\in A}{f(x)\ge c})=\infty$を満たす場合を示す．この$c$に対して

$\begin{align*}&B:=\set{x\in A}{f(x)\ge c}, \\&B_n:=\set{x\in A}{f_n(x)\ge c}\end{align*}$

とおく．$f_1\le f_2\le\dots$より$B_1\subset B_2\subset\dots$だから，測度の単調収束定理より

$\begin{align*}\lim_{n\to\infty}m(B_n)=m{\bra{\bigcup_{n=1}^{\infty}B_n}}=m(B)=\infty\end{align*}$

である．ただし，$\lim\limits_{n\to\infty}f_n=f$より$\bigcup_{n=1}^{\infty}B_n=B$に注意．

よって，$B_n\subset A$と，$B_n$上で$f_n(x)\ge c$であることに注意すれば

$\begin{align*}\int_{A}f_n(x)\,dx\ge\int_{B_n}f_n(x)\,dx\ge cm(B_n)\xrightarrow[]{n\to\infty}\infty\end{align*}$

なので，$\lim\limits_{n\to\infty}\dint_{A}f_n(x)\,dx=\infty$だから$\ge$の向きの不等式が成り立つ．

[場合２] 任意の$c>0$に対して，$m(\set{x\in A}{f(x)\ge c})<\infty$を満たす場合を示す．

$f$が恒等的に値０をとるなら$\dint_{A}f(x)\,dx=0$となって$\ge$の向きの不等式が成り立つから，以下$f$が恒等的には０でないときを示す．$A$を

$A=A_0\cup A_1\cup\dots\cup A_K$ ($K\ge1$)
$A_i\cap A_j=\emptyset$ ($i\neq j$)

を満たす任意の可測集合$A_0,A_1,\dots,A_n$で分割する．ただし，$\alpha_k:=\inf\limits_{x\in A_k}f(x)$が$\alpha_0<\alpha_1<\dots<\alpha_K$となるようにする．

なお，$K\ge1$とできることは$f$が恒等的には０でないことから分かる．

$B:=A\setminus A_0$とすると，場合分けの仮定から$\alpha_0=0$かつ$m(B)<\infty$をみたすことに注意する．

ここで，$A$上の非負値可測単関数$g$を

$\begin{align*}g=\sum_{k=0}^{K}\alpha_k I_{A_k}\end{align*}$

とする（$I_{A_k}$は定義関数）．また，任意に$0<\eta<\alpha_1$なる$\eta\in\R$をとり，

$\begin{align*}B_n:=\set{x\in A}{f_n(x)\ge g(x)-\eta}\end{align*}$

とおく．このとき，[場合１]と同様に$\lim\limits_{n\to\infty}m(B_n)=m(B)$が成り立つから，ある十分大きな$N\in\N$が存在して

$\begin{align*}|m(B)-m(B_N)|<\eta\iff m(B\setminus B_N)<\eta\end{align*}$

となる．$B_N\subset A$が成り立つことと，任意の$x\in B_n$に対して$f_n(x)\ge g(x)-\eta>0$が成り立つことに注意すると，[補題]と併せて

$\begin{align*}\int_{A}f_N(x)\,dx &\ge\int_{B_N}f_N(x)\,dx \\&\ge\int_{B_N}g(x)\,dx-\eta m(B_N) \\&\ge\int_{B_N}g(x)\,dx-\eta m(B)\end{align*}$

であり，この第１項について$B_N\subset B$に注意すると

$\begin{align*}\int_{B_N}g(x)\,dx&=\int_{B}g(x)\,dx-\int_{B\setminus B_N}g(x)\,dx \\&\ge\int_{B}g(x)\,dx-\int_{B\setminus B_N}\alpha_K\,dx \\&=\int_{B}g(x)\,dx-\alpha_K m(B\setminus B_N) \\&>\int_{B}g(x)\,dx-\alpha_K \eta\end{align*}$