以下は微分積分学に関する記事です.
微分積分学の基本
- 1. 上限supと下限inf|最大値max・最小値minより便利なヤツら
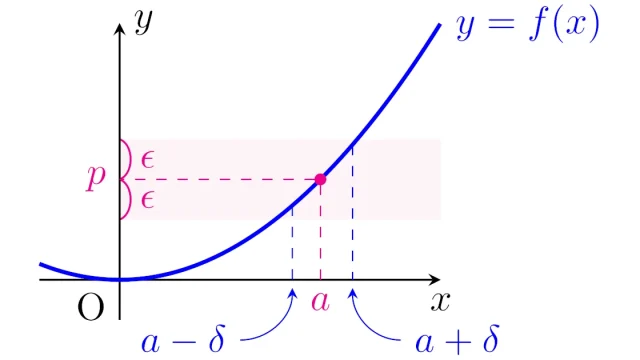
- 2. 数列の収束の定義(ε-N論法)|例題から考え方を理解しよう
- 3. 実数列の3種類の発散の定義と証明の例題
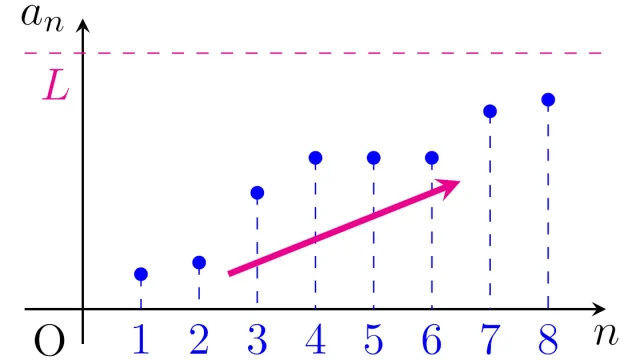
- 4. 単調有界実数列の収束定理|漸化式を解かずに極限を求める方法
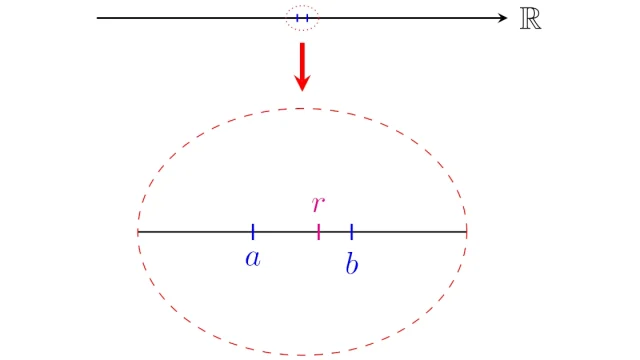
- 5. 有理数の稠密性の証明は「アルキメデスの性質」から
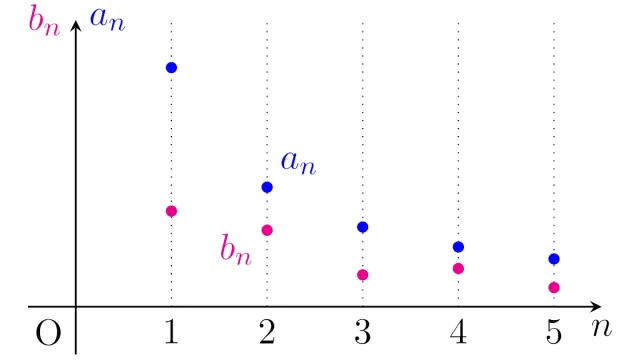
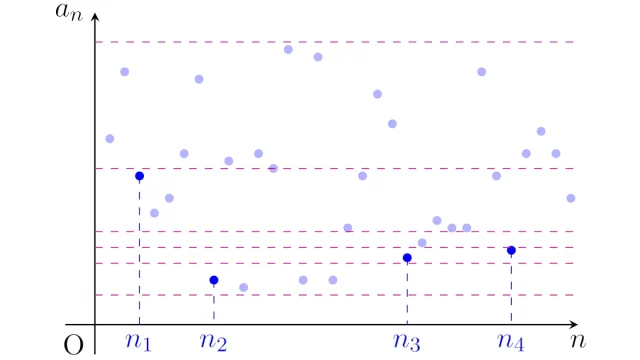
- 6. ボルツァーノ・ワイエルシュトラスの定理|区間縮小法による証明
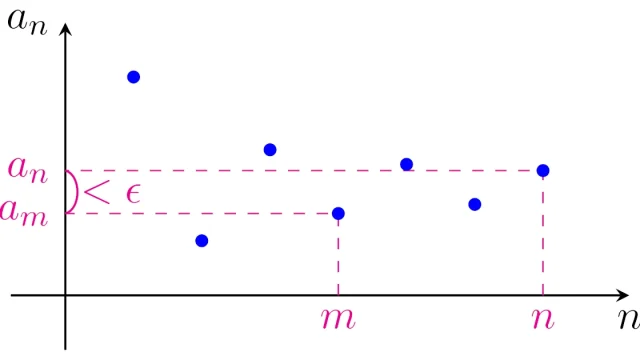
- 7. コーシー列の便利さ!収束列との関係と完備性
数列
微分法と積分法
- ラグランジュの未定乗数法|直感的に当たり前になる考え方
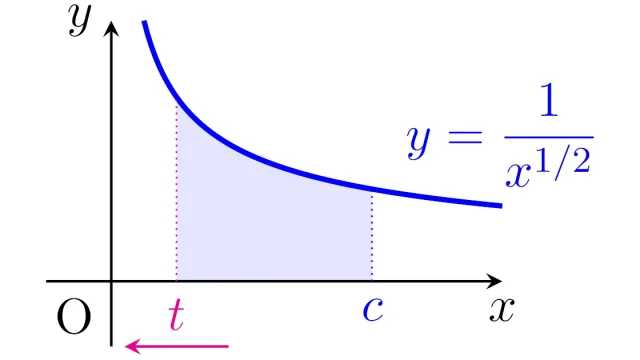
- ガウス関数のフーリエ変換1|コーシーの積分定理から計算する
- ガウス関数のフーリエ変換2|微分方程式を用いて計算する
- ガウス積分はどうやって求める?|極座標変換による計算
- 微分積分学の基本定理とその証明|微分と積分の関係を導出