関数の上限は1点の値を変えることでどこまでも大きくすることができます.例えば,関数$f:\R\to\R$を
\begin{align*}f(x)=\begin{cases}-x^2+1&(x\neq0),\\2&(x=0)\end{cases}\end{align*}
で定めると,この関数の値域の上限は$\sup\limits_{x\in\R}{f(x)}=2$ですね.
しかし,この関数は$x=0$での値が飛び跳ねているだけで,$f$の「本質的な上限」は
\begin{align*}\sup\limits_{x\in\R}(-x^2+1)=1\end{align*}
と言えそうです.このように考える上限を本質的上限といいます.
この記事では
- 本質的上限・本質的下限の定義
- 本質的上限・本質的下限の具体例
- 本質的上限・本質的下限の性質
を順に説明します.
「ルベーグ空間$L^p$の基本」の一連の記事
本質的上限・本質的下限の定義
冒頭の例のように,零集合上で値が「跳ねて」いるような部分を無視したときの上界を本質的上界といいます.
通常の上限と同様に,本質的上限は本質的上界の最小のものとして定義されます.
本質的上限の定義
可測集合$A\subset\R$上の可測関数$f$に対して,$S\in\R$が$f$の本質的上界(essential upper bound)であるとは
\begin{align*}m(\set{x\in A}{f(x)>S})=0\end{align*}
が成り立つことをいう.$f$の本質的上界が存在するとき,$f$は本質的に上に有界であるという.
言葉で説明すれば,関数$f$の値が$S$より大きくなるような$x$の集合の測度が0であるとき$S$を本質的上界という,ということですね.
例えば,冒頭の関数
\begin{align*}f(x)=\begin{cases}-x^2+1&(x\neq0),\\2&(x=0)\end{cases}\end{align*}
を考えると,
\begin{align*}m\bra{\set{x\in\R}{f(x)>\frac{3}{2}}}=m(\{0\})=0\end{align*}
なので,$\frac{3}{2}$は$f$の本質的上界のひとつですね.
このような本質的上界全部の集合の下限を本質的上限といいます.
可測集合$A\subset\R$上の本質的に上に有界な可測関数$f$に対して,$f$の本質的上界全部の集合の下限を$f$の本質的上限(essential supremum)といい,$\esssup\limits_{x\in A}{f(x)}$と表す:
\begin{align*}\esssup_{x\in A}{f(x)}:=\inf\set{S\in\R}{m(\set{x\in A}{f(x)>S})=0}\end{align*}
ただし,本質的上界が存在しないときは$\esssup\limits_{x\in A}{f(x)}=\infty$と定める.
本質的下限の定義
本質的下限も本質的上限と同様に以下のように定義されます.
可測集合$A\subset\R$上の可測関数$f$に対して,$s\in\R$が$f$の本質的下界(essential under bound)であるとは
\begin{align*}m(\set{x\in A}{f(x)<s})=0\end{align*}
が成り立つことをいう.$f$の本質的下界が存在するとき,$f$は本質的に下に有界であるという.
また,$f$の本質的下界の上限を$f$の本質的下限(essential infimum)といい,$\essinf\limits_{x\in A}{f(x)}$と表す:
\begin{align*}\essinf_{x\in A}{f(x)}:=\sup\set{s\in\R}{m(\set{x\in A}{f(x)<s})=0}\end{align*}
ただし,本質的上界が存在しないときは$\essinf\limits_{x\in A}{f(x)}=-\infty$と定める.
$f$が本質的に上に有界かつ本質的に下に有界であるとき,$f$は本質的有界であるといいます.
本質的上限・本質的下限の具体例
いくつか具体例を考えましょう.
例1(1点集合を無視する場合)
まずは冒頭の関数の本質的上限・本質的下限を求めましょう.
関数$f:\R\to\R$を
\begin{align*}f(x)=\begin{cases}-x^2+1&(x\neq0),\\2&(x=0)\end{cases}\end{align*}
と定める.$f$の本質的上限と本質的下限を求めよ.
この問題の関数$f$は$-x^2+1$とほとんど至る所で等しく,本質的上限は1と言えそうですね.
また,本質的下界は存在しそうになく,本質的下限は$-\infty$と言えそうですね.
[本質的上界]一般に一点集合は零集合なので,
\begin{align*}m(\set{x\in\R}{f(x)>1})
=m(\{0\})
=0\end{align*}
だから,1は$f$の本質的上界である.また,任意の$a<1$に対して
\begin{align*}&m(\set{x\in\R}{f(x)>a})
\\&=m\Bigl(\bigl(-\sqrt{1-a},\sqrt{1-a}\bigr)\Bigr)
\\&=2\sqrt{1-a}>0\end{align*}
だから,$a$は$f$の本質的上界でない.よって,$\esssup\limits_{x\in\R}{f(x)}=1$を得る.
[本質的下界]任意の$a\in\R$に対して
\begin{align*}&m(\set{x\in\R}{f(x)<a})
\\&=m\Bigl(\bigl(-\infty,-\sqrt{1-a}\bigr)\cup\bigl(\sqrt{1-a},\infty\bigr)\Bigr)
=\infty\end{align*}
だから,$a$は$f$の本質的下界でない.よって,$\essinf\limits_{x\in\R}{f(x)}=-\infty$を得る.
例2(可算集合を無視する場合)
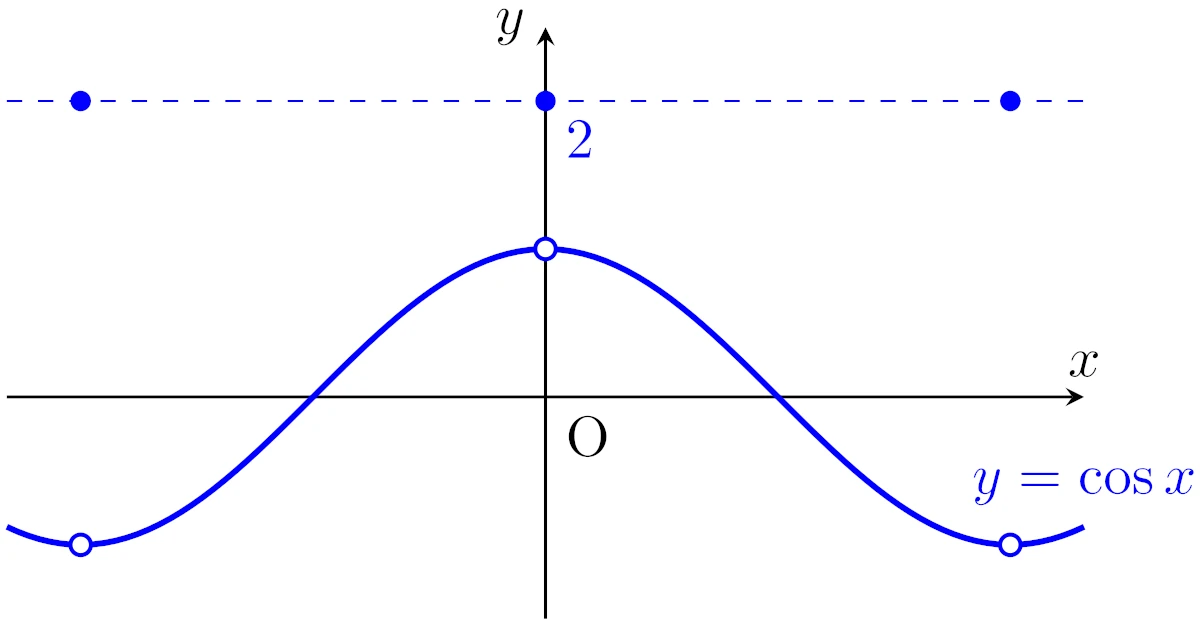
関数$f:\R\to\R$を
\begin{align*}f(x)=\begin{cases}\cos{x}&(x\neq0,\pm\pi,\pm2\pi,\dots),\\2&(x=0,\pm\pi,\pm2\pi,\dots)\end{cases}\end{align*}
と定める.$f$の本質的上限と本質的下限を求めよ.
$x=n\pi$で飛び抜けていますが,一般に可算集合は零集合なので,可算集合$\set{n\pi}{n\in\Z}$はルベーグ測度においては無視されます.
そのため,この問題の関数$f$は$\cos{x}$とほとんど至る所で等しく,本質的上限は1となりそうです.
また,本質的下限は通常の下限と一致して$-1$となりそうです.
[本質的上界]一般に可算集合は零集合なので,
\begin{align*}m(\set{x\in\R}{f(x)>1})
=m(\set{n\pi}{n\in\Z})
=0\end{align*}
だから,1は$f$の本質的上界である.また,任意の$a\in(0,1)$に対して
\begin{align*}&\set{x\in\R}{f(x)>a}
\\&=\bigcup_{n\in\Z}\bra{-\cos^{-1}{a}+2n\pi,\cos^{-1}{a}+2n\pi}\end{align*}
なので$m(\set{x\in\R}{f(x)>a})=\infty>0$だから,$a$は$f$の本質的上界でない.よって,$\esssup\limits_{x\in\R}{f(x)}=1$を得る.
[本質的下界]空集合は零集合なので,
\begin{align*}m(\set{x\in\R}{f(x)<-1})
=m(\emptyset)
=0\end{align*}
だから,$-1$は$f$の本質的上界である.また,任意の$a\in(-1,0)$に対して
\begin{align*}&\set{x\in\R}{f(x)<a}
\\&=\bigcup_{n\in\Z}\bra{-\cos^{-1}{a}+(2n+3)\pi,\cos^{-1}{a}+(2n+1)\pi}\end{align*}
なので$m(\set{x\in\R}{f(x)<a})=\infty>0$だから,$a$は$f$の本質的下界でない.よって,$\essinf\limits_{x\in\R}{f(x)}=-1$を得る.
例3(可算集合を無視する場合)
関数$f:\R\to\R$を
\begin{align*}f(x)=\begin{cases}x&(x\in\Q),\\0&(x\in\R\setminus\Q)\end{cases}\end{align*}
と定める.$f$の本質的上限と本質的下限を求めよ.
有理数全部の集合$\Q$は$\R$上で稠密ですが,$\Q$は可算集合なのでルベーグ測度では無視されます.
よって,この問題の関数$f$は0とほとんど至る所で等しく,本質的下限は0となりそうです.
[本質的上界]一般に可算集合は零集合なので,
\begin{align*}&m(\set{x\in\R}{f(x)<0})=m(\set{x\in\Q}{x<0})=0\end{align*}
だから0は$f$の本質的上界である.また,任意の$a<0$に対して
\begin{align*}\set{x\in\R}{f(x)>a}\supset(a,\infty)\end{align*}
だから,$m$の単調性と併せて
\begin{align*}&m(\set{x\in\R}{f(x)>a})\ge m((a,\infty))>0\end{align*}
だから,$a$は$f$の本質的上界でない.よって,$\esssup\limits_{x\in\R}{f(x)}=0$を得る.
[本質的下界]一般に可算集合は零集合なので,
\begin{align*}m(\set{x\in\R}{f(x)>0})=m(\set{x\in\Q}{x>0})=0\end{align*}
だから,0は$f$の本質的下界でもある.また,任意の$a>0$に対して
\begin{align*}\set{x\in\R}{f(x)<a}\supset(-\infty,a)\end{align*}
だから,$m$の単調性と併せて
\begin{align*}&m(\set{x\in\R}{f(x)<a})\ge m((-\infty,a))>0\end{align*}
だから,$a$は$f$の本質的下界でない.よって,$\essinf\limits_{x\in\R}{f(x)}=0$を得る.
本質的上限・本質的下限の性質
本質的上限・本質的下限の性質をいくつか紹介します.
本質的上限の最小性・本質的下限の最大性
上の定義では本質的上限$\esssup\limits_{x\in A}{f(x)}$は本質的上界全部の集合の「下限」と定義しましたが,本質的上界全部の集合は必ず最小値をもちます.また,本質的下限についても同様です.
[命題1]可測集合$A\subset\R$上の可測関数$f$が本質的に上に有界なら,本質的上限$\esssup\limits_{x\in A}{f(x)}$は$f$の本質的上界である.また,$f$が本質的に下に有界なら,本質的下限$\essinf\limits_{x\in A}{f(x)}$は$f$の本質的下界である.
正の整数$n$に対して
\begin{align*}A_n:=\set{x\in A}{f(x)>\esssup\limits_{x\in A}{f(x)}+\frac{1}{n}}\end{align*}
とおく.$\esssup\limits_{x\in A}{f(x)}+\dfrac{1}{n}$は$f$の本質的上界だから,任意の$n$に対して$m(A_n)=0$である.
さらに,$A_1\subset A_2\subset\dots$なので,測度の単調収束定理より
\begin{align*}&m\bra{\set{x\in A}{f(x)>\esssup_{x\in A}{f(x)}}}
\\&=m\bra{\bigcup_{n=1}^{\infty}A_n}
=\lim_{n\to\infty}m(A_n)=0\end{align*}
が成り立つ.よって,$\esssup\limits_{x\in A}{f(x)}$は$f$の本質的上界である.同様に
\begin{align*}A’_n:=\set{x\in A}{f(x)<\essinf_{x\in A}{f(x)}-\frac{1}{n}}\end{align*}
を考えれば,$\essinf\limits_{x\in A}{f(x)}$は本質的下界である.
本質的上限・本質的下限と零集合
本質的上限・本質的下限はうまく零集合を取り除いたときの上限・下限と言えるので以下が成り立ちます.
[命題2]可測集合$A\subset\R$上の可測関数$f$を考える.ある零集合$N\subset A$が存在して,任意の$x\in A\setminus N$に対して
\begin{align*}\essinf_{x\in A}{f(x)}\le f(x)\le\esssup_{x\in A}{f(x)}\end{align*}
が成り立つ.
証明には[命題1]を使いましょう.
$\esssup\limits_{x\in A}{f(x)}=\infty$なら右の不等式は常に成り立ち,$\essinf\limits_{x\in A}{f(x)}=\infty$なら左の不等式は常に成り立つから,以下では$f$が本質的有界な場合を示す.
$N_1,N_2\subset A$を
\begin{align*}&N_1:=\set{x\in A}{f(x)>\esssup_{x\in A}{f(x)}},
\\&N_2:=\set{x\in A}{f(x)<\essinf_{x\in A}{f(x)}}\end{align*}
とおく.[命題1]より$m(N_1)=m(N_2)=0$が成り立つので,$N:=N_1\cup N_2$とおくと$m$の劣加法性より
\begin{align*}m(N)\le m(N_1)+m(N_2)=0+0=0\end{align*}
である.また,$N_1$と$N_2$の定義より,任意の$x\in A\setminus N$に対して
\begin{align*}\essinf_{x\in A}{f(x)}\le f(x)\le\esssup_{x\in A}{f(x)}\end{align*}
が従う.
この[命題2]から次の系が従います.
可測集合$A\subset\R$上の可測関数$f$に対して
\begin{align*}\inf_{x\in A}{f(x)}\le\essinf_{x\in A}{f(x)}\le\esssup_{x\in A}{f(x)}\le\sup_{x\in A}{f(x)}\end{align*}
が成り立つ.
[命題2]より$\essinf\limits_{x\in A}{f(x)}\le\esssup\limits_{x\in A}{f(x)}$が成り立つ.
上界は本質的上界だから,$\sup{f}$の最小性より$\esssup\limits_{x\in A}{f(x)}\le\sup\limits_{x\in A}{f(x)}$が成り立つ.同様に$\inf\limits_{x\in A}{f(x)}\le\essinf\limits_{x\in A}{f(x)}$が成り立つ.
和の本質的上限・本質的下限
最後に$\esssup$の劣加法性と$\essinf$の優加法性を証明しておきます.
\begin{align*}&\esssup_{x\in A}{(f(x)+g(x))}\le\esssup_{x\in A}{f(x)}+\esssup_{x\in A}{g(x)},
\\&\essinf_{x\in A}{(f(x)+g(x))}\ge\essinf_{x\in A}{f(x)}+\essinf_{x\in A}{g(x)}\end{align*}
が成り立つ.
[命題2]より,ある零集合$N_f,N_g\subset A$が存在して,
- 任意の$x\in A\setminus N_f$に対して$f(x)\le\esssup\limits_{x\in A}{f(x)}$
- 任意の$x\in A\setminus N_g$に対して$g(x)\le\esssup\limits_{x\in A}{g(x)}$
が成り立つ.よって,$N:=N_f\cup N_g$とおくと,任意の$x\in A\setminus N$に対して
\begin{align*}f(x)+g(x)\le\esssup_{x\in A}{f(x)}+\esssup_{x\in A}{g(x)}\end{align*}
が成り立つ(零集合の和集合である$N$も零集合であることに注意).よって,本質的上限の最小性より
\begin{align*}\esssup_{x\in A}{(f(x)+g(x))}\le\esssup_{x\in A}{f(x)}+\esssup_{x\in A}{g(x)}\end{align*}
が従う.同様に本質的下限についての不等式も従う.



コメント