2026年度の京都大学 理学研究科 数学・数理解析専攻の大学院入試問題の専門科目の解答の方針と解答例です.
問題は13題あり
- 数学系は第1問〜第11問から
- 数理解析系は第1問〜第13問から
2題を選択して解答します.試験時間は2時間30分です.この記事では,第6〜8問について解説しています.
ただし,公式に採点基準などは発表されていないため,本稿の解答が必ずしも正解になるとは限りません.ご注意ください.
また,十分注意して解答を作成していますが,論理の飛躍・誤りが残っている場合があります.
なお,過去問は京都大学の数学教室の過去問題のページから入手できます.
第6問(測度論)
$(X,\mathcal{M},\mu)$は$\mu(X)<\infty$を満たす測度空間とし,$L$は正の実数とする.$X$上の実数値または複素数値$\mu$-可積分関数$f$について,次の命題Pを考える.
命題P:$\abs{\dint_A f\,d\mu}\le L\mu(A)$が任意の$A\in\mathcal{M}$について成り立つならば,\begin{align*}|f(x)|\le L,\quad \text{$\mu$-a.e. $x$}\end{align*}が成り立つ.
- $f$が実数値であるとき,命題Pを証明せよ.
- $f$が複素数値であるとき,命題Pを証明せよ.
本質的には,どんな測度正の可測集合$A$上でも関数$f$の平均の絶対値が$L$以下であれば,ほとんど至るところで関数$f$の絶対値が$L$以下であることを示す問題です.
解答の方針とポイント
$f$が実数値関数のときは直観的には成り立っていそうで,それをきちんと論証できるかが問題です.また,$f$が複素数値関数のときは,全ての偏角方向で(1)を適用すればよさそうですが,零集合の扱いに気をつける必要があります.
関数の絶対値を正成分と負成分に分けて考える
$f$が実数値関数の場合は,直観的にも測度正の可測集合$A$上で$f(x)>L$となっていれば,$A$上での$f$の平均の絶対値は$L$より大きくなっていそうですから,(1)は対偶を示しましょう.
ほとんど至るところで$|f(x)|\le L$であることの定義は$\mu(\set{x\in X}{|f(x)|>L})=0$ですから,この否定は
\begin{align*}\mu(\set{x\in X}{|f(x)|>L})>0\quad\dots(*)\end{align*}
ですね.この$(*)$が成り立つとき,$A=\set{x\in X}{|f(x)|>L}$とおくと$\int_{A} |f|\,d\mu>L\mu(A)$であることは分かります.しかし,我々が示さないといけない
\begin{align*}\abs{\int_A f\,d\mu}>L\mu(A)\end{align*}
は積分の外に絶対値があるので,これだけでは証明できません.
$\int_A |f|\,d\mu>L\mu(A)$から$\abs{\int_A f\,d\mu}>L\mu(A)$が示せないのは,$|f|$は$f$の正成分$f_+$と負成分$f_-$を$|f|=f_{+}+f_{-}$と合わせていることが理由ですから,正成分$f_+$と負成分$f_-$に分けて$f$の積分を考えることがポイントになりそうです.
$X$を集合とする.実数値関数$f:X\to\R$に対して,
\begin{align*}f_+(x)=\max\{f(x),0\},\quad
f_-(x)=\max\{-f(x),0\}\end{align*}
で定まる関数$f_+:X\to[0,\infty)$を$f$の正成分,関数$f_-:X\to[0,\infty)$を$f$の負成分という.
そこで,対偶の仮定$(*)$から「正成分$f_+$と負成分$f_-$のいずれかは測度正の集合上で$L$より大きい」ということを用いれば解決しそうです.
\begin{align*}\mu(\set{x\in X}{f_+(x)>L})>0\end{align*}
のときは,$A=\set{x\in X}{f_+(x)>L}$とすれば
\begin{align*}\abs{\int_{A} f(x)\,d\mu(x)}=\int_{A} f_+(x)\,d\mu(x)>L\mu(A)\end{align*}
となって対偶が成り立ちますし,$\mu(\set{x\in X}{f_+(x)>L})=0$のときは負成分に注目すれば同様に証明できますね.
複素数値の場合も(1)から各偏角方向で$|f(x)|$を評価できる
たとえば,$f=g+ih$と$f$を実部$g$と虚部$h$に分けると,任意の$A\in\mathcal{M}$に対して$\abs{\int_A f\,d\mu}\le L$なら
\begin{align*}\abs{\int_A g\,d\mu}\le\abs{\int_A g\,d\mu+i\int_A h\,d\mu}\le\abs{\int_A f\,d\mu}\le L\end{align*}
となるので,(1)よりほとんど至るところで$|g|\le L$が成り立ちます.すなわち,ほとんど全ての$x\in X$に対して$f(x)$は実軸方向に原点から距離$L$より離れていないことが分かります.
同様に$f(x)$を原点中心に偏角$\theta$回転させた$\operatorname{Re}(f(x)e^{i\theta})$について(1)を用いれば,ほとんど全ての$x\in X$に対して$f(x)$の偏角$-\theta$方向に原点から距離$L$より離れていないことが分かります.
ただし,各$\theta$ごとに「ほとんど全ての$x$」が定まるので,これだけではまだ示せていません.
たかだか可算個の零集合の和集合は零集合
大部分の$x\in X$に対して,もともと$|\operatorname{Re}(f(x)e^{i\theta})|\le L$であれば,ほんの少し$\theta$を変えて$\theta’$にしても$|\operatorname{Re}(f(x)e^{i\theta’})|\le L$です(回転の連続性).
そのため,任意の$\theta\in[0,\pi)\cap\Q$($[0,\pi)$の稠密可算部分集合)で
\begin{align*}|\operatorname{Re}(f(x)e^{i\theta})|\le L,\quad\text{$\mu$-a.e. $x$}\end{align*}
が成り立ちさえすれば,回転が連続であることと併せて,全ての$\theta\in[0,\pi)$に対しても成り立ちますね.
さて,可算個の零集合の和集合も零集合であることから,
\begin{align*}N=\bigcup_{\theta\in[0,\pi)\cap\Q}\set{x\in X}{|\operatorname{Re}(f(x)e^{i\theta})|>L}\end{align*}
も零集合です.すなわち,$x\notin N$なら,全ての$\theta\in[0,\pi)\cap\Q$に対して$|\operatorname{Re}(f(x)e^{i\theta})|\le L$が成り立つことが分かります.
以上を併せて,$x\notin N$なら,全ての$\theta\in[0,\pi)$に対して$|\operatorname{Re}(f(x)e^{i\theta})|\le L$が成り立つことが分かるので,全ての方向に$f(x)$は原点から距離$L$より離れていないことが分かります.
解答例
(1)の解答
実数値関数$F$に対して,$F$の正成分と負成分をそれぞれ$F_+$, $F_-$と表す.また,$|F|$の分布関数を$\mu_F$と表す:
\begin{align*}\mu_F:[0,\infty)\to[0,\mu(X)];\lambda\mapsto\mu(\set{x\in X}{|F(x)|>\lambda}).\end{align*}
対偶を示す.$|f(x)|\le L$, $\mu$-a.e. $x$が成り立たないとする.このことは$\mu_f(L)>0$と同値で,このとき$\mu_f(L)=\mu_{f_+}(L)+\mu_{f_-}(L)$と併せて,$0<\mu_{f_+}(L)$または$0<\mu_{f_-}(L)$が成り立つ.
$0<\mu_{f_+}(L)$が成り立つとき,
\begin{align*}A_n=\set{x\in X}{f_+(x)>L+\frac{1}{n}}\end{align*}
とする($n=1,2,\dots$)と,$A_1\subset A_2\subset\dots$が成り立つから,測度の連続性より
\begin{align*}\lim\limits_{n\to\infty}\mu(A_n)=\mu\bra{\bigcup_{n=1}^{\infty}A_n}=\mu_{f_+}(L)>0\end{align*}
が成り立つ.よって,ある$N\in\N$が存在して$\mu(A_N)>0$が成り立つから,
\begin{align*}\abs{\int_{A_N}f\,d\mu}=\int_{A_N}f_+\,d\mu\ge\int_{A_N}\bra{L+\frac{1}{N}}\,d\mu=\bra{L+\frac{1}{N}}\mu(A_N)\end{align*}
を得る.
一方,$0<\mu_{f_+}(L)$が成り立たないとき,$0<\mu_{f_-}(L)$だから,同様にある$N’\in\N$が存在して$\mu_{f_-}(L+\frac{1}{N’})>0$が成り立ち,
\begin{align*}\abs{\int_{\{f_-(x)>L+\frac{1}{N’}\}}f\,d\mu}\ge\bra{L+\frac{1}{N’}}\mu\bra{\set{x\in X}{f_-(x)>L+\frac{1}{N’}}}\end{align*}
が成り立つ.
以上より,ある$A\in\mathcal{M}$が存在して$\abs{\dint_A f\,d\mu}>L\mu(A)$が成り立つから,対偶が示された.
(2)の解答
$\abs{\dint_A f\,d\mu}\le L\mu(A)$が任意の$A\in\mathcal{M}$について成り立つとする.$[0,\pi)\cap\Q$は可算集合だから$[0,\pi)\cap\Q=\{\theta_1,\theta_2,\dots\}$とする.任意の$n\in\{1,2,\dots\}$, $A\in\mathcal{M}$に対して,
\begin{align*}&\abs{\int_{A}\operatorname{Re}(e^{i\theta_n}f)\,d\mu}=\abs{\operatorname{Re}\int_{A}(e^{i\theta_n}f)\,d\mu}
\\&\le\abs{\int_{A}e^{i\theta_n}f\,d\mu}=\abs{\int_{A}f\,d\mu}\le L\mu(A)\end{align*}
が成り立つ.$\operatorname{Re}(e^{i\theta_n}f)$は実数値関数だから,(1)より
\begin{align*}|\operatorname{Re}(e^{i\theta_n}f(x))|\le L,\quad \text{$\mu$-a.e. $x$}\end{align*}
が成り立つ.すなわち,ある零集合$N_n\subset X$が存在して,
\begin{align*}x\in X\setminus N_n\Ra|\operatorname{Re}(e^{i\theta_n}f(x))|\le L\end{align*}
が成り立つ.可算個の零集合の和集合も零集合だから$N=\bigcup_{n=1}^{\infty}N_n$も零集合である.
任意の$x\in X\setminus N$に対して,関数
\begin{align*}[0,2\pi)\to[0,\infty);\theta\mapsto|\operatorname{Re}(e^{i\theta}f(x))|\end{align*}
は連続で,$[0,\pi)\cap\Q$は$[0,\pi)$で稠密だから,任意の$\theta\in[0,\pi)$に対して$|\operatorname{Re}(e^{i\theta}f(x))|\le L$が成り立つ.
一般に,$z\in\C$が$|z|\le L$を満たすことと,任意の$\theta\in[0,2\pi)$に対して$|\operatorname{Re}(e^{i\theta}z)|\le L$が成り立つことは同値だから,任意の$x\in X\setminus N$に対して$|f(x)|\le L$が成り立つ.
第7問(複素解析・関数解析)
$\mathbb{D}=\{z\in\C:|z|<1\}$とする.$H^\infty(\mathbb{D})$を$\mathbb{D}$上の有界正則関数全体のなす複素バナッハ空間とし,$f\in H^\infty(\mathbb{D})$のノルムを
\begin{align*}\|f\|_\infty=\sup_{z\in\mathbb{D}}|f(z)|\end{align*}
とする.$0<r\le1$に対して,作用素$T_r:H^\infty(\mathbb{D})\to H^\infty(\mathbb{D})$を
\begin{align*}(T_rf)(z)=\int_0^r f(tz)\,dt\end{align*}
と定める.
- $0<r<s<1$を固定する.次の条件$(*)$を満たす連続関数\begin{align*}k:[0,r]\times[0,2\pi]\times\mathbb{D}\to\C\end{align*}が存在することを示せ.
$(*)$任意の$f\in H^\infty(\mathbb{D})$と$z\in\mathbb{D}$に対して\begin{align*}(T_rf)(z)=\int_0^r \int_0^{2\pi}k(t,\theta,z)f(se^{i\theta})\,d\theta dt.\end{align*}ただし$i$は虚数単位とする. - $T_1$はコンパクト作用素であることを示せ.
$\mathbb{D}$上の有界正則関数$f$に対して,$f$の線分$\overline{0z}\subset\C$上の積分$\int_0^1 f(tz)\,dt$で定まる$z$の関数を返す作用素$T_1$がコンパクトであることを示す問題です.
解答の方針とポイント
(1)は見るからに平均値の性質(コーシーの積分公式)が使えそうですね.(2)は$H^\infty(\mathbb{D})$上の有界点列$\{f_n\}$に対して,$\{T_1f_n\}$が収束部分列をもつことを示しましょう.
コーシーの積分公式と平均値の性質
領域$D$上の正則関数$\phi:D\to\C$に対して,$\alpha$中心,半径$r$の閉円板が$D$に含まれるときコーシーの積分公式
\begin{align*}\phi(\alpha)=\frac{1}{2\pi i}\int_{|z-\alpha|=r}\frac{\phi(z)}{z-\alpha}\,dz\end{align*}
が成り立ちます.$z=\alpha+re^{i\theta}$と置き換えると,右辺は「$\alpha$中心の円周上の値の平均」となり,この正則関数の性質を(正則関数の)平均値の性質といいます.
[平均値の性質]領域$D$と正則関数$\phi:D\to\C$を考える.$\set{z\in\C}{|z-a|\le r}\subset D$なる$a\in D$, $r>0$に対して,
\begin{align*}\phi(a)=\frac{1}{2\pi}\int_{0}^{2\pi}\phi(a+re^{i\theta})\,d\theta\end{align*}
が成り立つ.
コーシーの積分定理より,被積分関数が正則な領域上では積分経路を連続的に変化させても値は変わりませんから,積分経路の円周の中心は$a$である必要はありません.
積分経路が円周である必要もありませんね.
本問(1)では原点中心で半径$s$の円周$|z|=s$上での積分の形
\begin{align*}(T_rf)(z)=\int_0^r \int_0^{2\pi}k(t,\theta,z)f(se^{i\theta})\,d\theta dt.\end{align*}
にするので,コーシーの積分公式で積分経路を円周$|z|=s$に変形すればよいですね.
コンパクト作用素
コンパクト作用素は有界点列または有界集合を用いて,次のように定義されます.
ノルム空間$X$, $Y$に対して,$\mathcal{D}(T)=X$を満たす線形作用素$T:X\to Y$がコンパクト作用素であるとは,次の同値な2つの条件のいずれか(したがって両方)を満たすことをいう.
- $X$の任意の有界点列$\{f_n\}$に対して,$Y$の点列$\{Tf_n\}$は収束部分列をもつ.
- 任意の有界集合$A\subset X$に対して,$\overline{TA}$は点列コンパクトである.
有界点列を用いて$T_1$のコンパクト性を示すなら,任意に$H^\infty(\mathbb{D})$の有界点列$\{f_n\}$をとり$\{T_1f_n\}$が収束部分列をもつことを示すことになるので,
\begin{align*}(T_1f_n)(z)=\int_{0}^{1}f_n(tz)\,dt\end{align*}
を考える必要があります.$\{f_n\}$は有界なので,$r$が十分1に近ければ$n$によらず
\begin{align*}\abs{\int_{r}^{1}f_n(tz)\,dt}\le(1-r)M\end{align*}
はいくらでも小さくできるので,本質的には$\int_{0}^{r}f_n(tz)\,dt=(T_rf_n)(z)$が$n\to\infty$で小さくなることを示せばよいですね.
コンパクト作用素$X\to Y$全部の空間は閉なので,各$r\in(0,1)$に対して$T_r$がコンパクト作用素であることと$\|T_r-T\|\to0$を示しても,$T$がコンパクト作用素であることが分かりますね.
$\frac{1}{1-\zeta}$の冪級数展開
本問(1)より,$0<r<1$なら$s\in(r,1)$をとれば
\begin{align*}(T_rf_n)(z)=\frac{1}{2\pi}\int_{0}^{r}\bra{\int_{0}^{2\pi}\frac{f_n(se^{i\theta})}{1-\frac{tz}{se^{i\theta}}}\,d\theta}\,dt\end{align*}
となります.ここで,$\frac{1}{1-\frac{tz}{se^{i\theta}}}$が$\frac{1}{1-\zeta}$の形をしていることに気付きます.
関数$\frac{1}{1-\zeta}$は$|\zeta|<1$で$\sum\limits_{m=0}^{\infty}\zeta^m$と冪級数展開できることはよく用いるので,当たり前にしておきましょう.いま,$t$, $\theta$について一様に$|\frac{tz}{se^{i\theta}}|<1$ですから,項別積分可能で
\begin{align*}(T_rf_n)(z)=\frac{1}{2\pi}\sum_{m=0}^{\infty}\frac{r^{m+1} z^m}{m+1}\int_{0}^{2\pi}\frac{f_n(se^{i\theta})}{(se^{i\theta})^m}\,d\theta\quad\dots(\star)\end{align*}
と変形できます.さらに,$t$, $\theta$について一様に
\begin{align*}\abs{\frac{r^{m+1} z^m}{m+1}\int_{0}^{2\pi}\frac{f_n(se^{i\theta})}{(se^{i\theta})^m}\,d\theta}\le2\pi r\bra{\frac{r}{s}}^mM\end{align*}
と評価できるので,$|\frac{r}{s}|<1$より級数$(\star)$は絶対一様収束します.よって,十分大きく$K\in\N$をとれば
\begin{align*}\abs{\frac{1}{2\pi}\sum_{m=K+1}^{\infty}\frac{r^{m+1} z^m}{m+1}\int_{0}^{2\pi}\frac{f_n(se^{i\theta})}{(se^{i\theta})^m}\,d\theta}\end{align*}
もいくらでも小さくできます.したがって,さらに本質的には級数$(\star)$の第$K$項までの部分和が$n\to\infty$で小さくなることを示すことに帰着しますね.
正則関数の微分係数の積分表示
正則関数$\phi$のテイラー展開$\phi(z)=\sum\limits_{m=0}^{\infty}a_m(z-\alpha)^m$では,コーシーの積分公式を直接を変形してテイラー展開できることを示します.そのため,テイラー展開の係数$a_m$が
\begin{align*}a_m=\frac{1}{2\pi i}\int_{|z-\alpha|=r}\frac{\phi(z)}{(z-\alpha)^{m+1}}\,dz\end{align*}
であることが同時に得られます.よって,$a_m=\frac{f^{(m)}(\alpha)}{m!}$と併せて,平均値の性質のように$z=\alpha+se^{i\theta}$と置き換えると
\begin{align*}f^{(m)}(\alpha)&=\frac{m!}{2\pi i}\int_{|z-\alpha|=r}\frac{\phi(z)}{(z-\alpha)^{m+1}}\,dz
\\&=\frac{m!}{2\pi}\int_{0}^{2\pi}\frac{\phi(\alpha+se^{i\theta})}{(se^{i\theta})^{m}}\,d\theta\end{align*}
が得られます.したがって,本問(2)での級数$(\star)$の第$K$項までの部分和は
\begin{align*}\sum_{m=0}^{K}\frac{r^{m+1}f_n^{(m)}(0)}{m!(m+1)}z^m\end{align*}
となり,あとは全ての$m\in\{0,1,\dots,K\}$に対して複素数列$\{f_{n_k}^{(m)}(0)\}$が収束するような部分列$\{f_{n_k}\}$をボルツァーノ-ワイエルシュトラスの定理と対角線論法によって取ることで$\{T_1f_{n_k}\}$の収束が従います.
解答例
(1)の解答
任意に$f\in H^\infty(\mathbb{D})$と$z\in\mathbb{D}$をとる.任意の$t\in[0,r]$に対して,$tz$は開円板$\set{z\in\C}{|z|<s}$に属するから,コーシーの積分公式より
\begin{align*}f(tz)=\frac{1}{2\pi i}\int_{|\zeta|=s}\frac{f(\zeta)}{\zeta-tz}\,d\zeta\end{align*}
が成り立つ.$\zeta=se^{i\theta}$とおくと,$\frac{d\zeta}{d\theta}=sie^{i\theta}$なので
\begin{align*}f(tz)&=\frac{1}{2\pi i}\int_{0}^{2\pi}\frac{f(se^{i\theta})}{se^{i\theta}-tz}\cdot sie^{i\theta}\,d\theta
\\&=\frac{1}{2\pi}\int_{0}^{2\pi}\frac{se^{i\theta}f(se^{i\theta})}{se^{i\theta}-tz}\,d\theta\end{align*}
が成り立つ.よって,$(*)$を満たす連続関数$k:[0,r]\times[0,2\pi]\times\mathbb{D}\to\C$は
\begin{align*}k(t,\theta,z)=\frac{se^{i\theta}}{2\pi(se^{i\theta}-tz)}\end{align*}
ととれる.
(2)の解答
任意に$H^\infty(\mathbb{D})$の有界点列$\{f_n\}_{n\in\N}$をとる.このとき,ある$M>0$が存在して,任意の$n\in\N$に対して$\|f_n\|_{\infty}\le M$が成り立つ.
任意に$\epsilon>0$をとる.$r=\max\{1-\frac{\epsilon}{8M},\frac{1}{2}\}$とおく.任意の$n\in\N$と$z\in\mathbb{D}$に対して
\begin{align*}(T_1f_n)(z)=(T_rf_n)(z)+\int_{r}^{1}f_n(tz)\,dt\end{align*}
であり,この第2項は
\begin{align*}\abs{\int_{r}^{1}f_n(tz)\,dt}&\le\int_{r}^{1}|f_n(tz)|\,dt\le\int_{r}^{1}M\,dt
\\&=(1-r)M\le\frac{\epsilon}{8M}\cdot M=\frac{\epsilon}{8}\end{align*}
と評価できる.一方,第1項は$s=\frac{1+r}{2}$とおくと,$r<s<1$だから(1)より
\begin{align*}(T_rf_n)(z)
&=\frac{1}{2\pi}\int_{0}^{r}\bra{\int_{0}^{2\pi}\frac{se^{i\theta}f_n(se^{i\theta})}{se^{i\theta}-tz}\,d\theta}\,dt
\\&=\frac{1}{2\pi}\int_{0}^{r}\bra{\int_{0}^{2\pi}\frac{f_n(se^{i\theta})}{1-\frac{tz}{se^{i\theta}}}\,d\theta}\,dt\end{align*}
となる.関数$\frac{1}{1-\zeta}$の冪級数展開$\sum\limits_{m=0}^{\infty}\zeta^m$は収束半径1で,$t\in[0,r]$, $\theta\in[0,2\pi]$に対して一様に$|\frac{tz}{se^{i\theta}}|\le|\frac{t}{s}|<1$だから,
\begin{align*}(T_rf_n)(z)
&=\frac{1}{2\pi}\sum_{m=0}^{\infty}\int_{0}^{r}\bra{\int_{0}^{2\pi}\frac{t^m z^m f_n(se^{i\theta})}{(se^{i\theta})^m}\,d\theta}\,dt
\\&=\frac{1}{2\pi}\sum_{m=0}^{\infty}\frac{r^{m+1} z^m}{m+1}\int_{0}^{2\pi}\frac{f_n(se^{i\theta})}{(se^{i\theta})^m}\,d\theta\end{align*}
と項別積分可能である.ここで,任意の$m\in\{0,1,2,\dots\}$に対して,
\begin{align*}&\abs{\frac{r^{m+1} z^m}{m+1}\int_{0}^{2\pi}\frac{f_n(se^{i\theta})}{(se^{i\theta})^m}\,d\theta}
\\&\le\frac{r^{m+1}|z|^m}{m+1}\int_{0}^{2\pi}\frac{|f_n(se^{i\theta})|}{|se^{i\theta}|^m}\,d\theta
\\&\le2\pi r\bra{\frac{r}{s}}^mM\end{align*}
であり,$|\frac{r}{s}|<1$だから,ある$K\in\N$が存在して,任意の$z\in\mathbb{D}$に対して,
\begin{align*}\abs{\frac{1}{2\pi}\sum_{m=K+1}^{\infty}\frac{r^{m+1}z^m}{m+1}\int_{0}^{2\pi}\frac{f_n(se^{i\theta})}{(se^{i\theta})^m}\,d\theta}<\frac{\epsilon}{8}\end{align*}
が成り立つ.また,任意の$m\in\{0,1,\dots,K\}$に対して,
\begin{align*}&\frac{1}{2\pi}\int_{0}^{2\pi}\frac{f_n(se^{i\theta})}{(se^{i\theta})^m}\,d\theta
=\frac{1}{2\pi}\int_{|\zeta|=s}\frac{f_n(\zeta)}{\zeta^m}\cdot\frac{1}{i\zeta}\,d\zeta
\\&=\frac{1}{2\pi i}\int_{|\zeta|=s}\frac{f_n(\zeta)}{(\zeta-0)^{m+1}}\,d\zeta=\frac{f_n^{(m)}(0)}{m!}\end{align*}
である.以上より,任意の$k,\ell\in\N$, $z\in\mathbb{D}$に対して,
\begin{align*}&|T_1f_{n_k}(z)-T_1f_{n_\ell}(z)|
\\&\le\abs{\sum_{m=0}^{K}\frac{r^{m+1}f_{n_k}^{(m)}(0)}{m!(m+1)}z^m-\sum_{m=0}^{K}\frac{r^{m+1}f_{n_\ell}^{(m)}(0)}{m!(m+1)}z^m}
\\&\quad+\abs{\sum_{m=K+1}^{\infty}\frac{r^{m+1}f_{n_k}^{(m)}(0)}{m!(m+1)}z^m}+\abs{\sum_{m=K+1}^{\infty}\frac{r^{m+1}f_{n_\ell}^{(m)}(0)}{m!(m+1)}z^m}
\\&\quad+\abs{\int_{r}^{1}f_{n_k}(tz)\,dt}+\abs{\int_{r}^{1}f_{n_\ell}(tz)\,dt}
\\&\le\abs{\sum_{m=0}^{K}\frac{r^{m+1}(f_{n_k}^{(m)}(0)-f_{n_\ell}^{(m)}(0))}{m!(m+1)}z^m}+\frac{\epsilon}{2}\end{align*}
となる.
ここで,$m\in\{0,1,2,\dots,K\}$とする.任意の$n\in\N$に対して,
\begin{align*}|f_n^{(m)}(0)|&=\abs{\frac{m!}{2\pi}\int_{0}^{2\pi}\frac{f_n(se^{i\theta})}{(se^{i\theta})^m}\,d\theta}
\\&\le\frac{m!}{2\pi}\int_{0}^{2\pi}\frac{|f_n(se^{i\theta})|}{|se^{i\theta}|^m}\,d\theta
\\&\le\frac{m!}{2\pi s^m}\int_{0}^{2\pi}M\,d\theta
\le \frac{m!M}{s^m}\end{align*}
である.以下のように$\{f_n\}_{n\in\N}$の部分列$\{f_{n_{m,k}}\}_{k\in\N}$を帰納的に定める.
- 複素数列$\{f_n(0)\}_{n\in\N}$は有界だから,ボルツァーノ-ワイエルシュトラスの定理より収束部分列$\{f_{n_{1,k}}(0)\}_{k\in\N}$をとる.
- ある$m\in\{0,1,2,\dots,K-1\}$に対して,$\{f_n\}_{n\in\N}$の部分列$\{f_{n_{m,k}}\}_{k\in\N}$がとれたとする.複素数列$\{f^{(m+1)}_{n_{m,k}}(0)\}_{k\in\N}$は有界だから,ボルツァーノ-ワイエルシュトラスの定理より収束部分列$\{f^{(m+1)}_{n_{m+1,k}}(0)\}_{k\in\N}$をとる.
このとき,$f_{n_k}=f_{n_{k,k}}$とおくと,$\{f_n\}_{n\in\N}$の部分列$\{f_{n_k}\}_{k\in\N}$が得られる.$\{f_{n_k}^{(m)}(0)\}_k$は収束列(コーシー列)だから,ある$N_m\in\N$が存在して
\begin{align*}k,\ell>N_m\Ra|f_{n_k}^{(m)}(0)-f_{n_\ell}^{(m)}(0)|<\frac{\epsilon}{2K}\end{align*}
が成り立つ.よって,$N=\max\limits_{m\in\{0,1,\dots,K\}}N_m$とおくと,$k,\ell>N$のとき,$z\in\mathbb{D}$によらず
\begin{align*}&\abs{\sum_{m=0}^{K}\frac{r^{m+1}(f_{n_k}^{(m)}(0)-f_{n_\ell}^{(m)}(0))}{m!(m+1)}z^m}
\\&\le\sum_{m=0}^{K}\frac{r^{m+1}|f_{n_k}^{(m)}(0)-f_{n_\ell}^{(m)}(0)|}{m!(m+1)}|z|^m
\\&\le\sum_{m=0}^{K}\frac{\epsilon}{2K}=\frac{\epsilon}{2}\end{align*}
が成り立つ.
以上より,$k,\ell>N$のとき$\|T_1f_{n_k}-T_1f_{n_\ell}\|_\infty<\epsilon$となるから,$\{T_1f_{n_k}\}_k$は$H^\infty(\mathbb{D})$のコーシー列である.$H^\infty(\mathbb{D})$の完備性より収束列である.よって,$T_1$はコンパクトである.
第8問(微分方程式)
$\Omega\subset\R^3$は$C^\infty$級の境界$\partial\Omega$をもつ有界領域とし,$\overline{\Omega}$を$\Omega$の閉包とする.$\nu(x)=(\nu_1(x),\nu_2(x),\nu_3(x))$を$x\in\partial\Omega$における$\partial\Omega$の外向き単位法線ベクトルとする.関数$u:\overline{\Omega}\times[0,\infty)\to\R$は連続で$\Omega\times(0,\infty)$上$C^\infty$級であり,かつ$u$の各階の偏導関数は$\overline{\Omega}\times[0,\infty)$上の有界な連続関数として拡張でき,さらに$u$は次を満たすとする:
\begin{align*}\left\{\begin{aligned}\frac{\partial u}{\partial t}-\Delta{u}&=0,&&(x,t)\in\Omega\times(0,\infty)
\\\frac{\partial u}{\partial \nu}&=0,&&(x,t)\in\partial\Omega\times(0,\infty)
\\\int_{\Omega}u(x,0)\,dx&\neq0.&\end{aligned}\right.\end{align*}
ただし,$\Delta{u}=\displaystyle\sum_{k=1}^{3}\frac{\partial^2 u}{\partial x_k^2}$, $\dfrac{\partial u}{\partial \nu}=\displaystyle\sum_{k=1}^{3}\frac{\partial u}{\partial x_k}\nu_k$である.関数$M(t)$, $E(t)$を
\begin{align*}M(t)=\int_{\Omega}u(x,t)\,dx,&&E(t)=\int_{\Omega}|u(x,t)|^2\,dx\end{align*}
により定めるとき,以下の(1), (2), (3), (4)を示せ.
- $M(t)$は$t$によらない定数関数である.
- 任意の$t>0$に対して,$E(t)\le E(0)$が成り立つ.
- $H(t)=\log{E(t)}$とおくとき,任意の$t>0$に対して,$\dfrac{d^2 H}{dt^2}(t)\ge0$が成り立つ.
- 任意の$T>0$と$t\in(0,T)$に対して,$E(t)\le E(0)^{1-\frac{t}{T}}E(T)^{\frac{t}{T}}$が成り立つ.
熱方程式$\frac{\partial u}{\partial t}=\Delta{u}$の質量$M(t)$とエネルギー$E(t)$の評価に関する問題です.
解答の方針とポイント
法線方向微分の境界条件(ノイマン境界条件)があるので,部分積分とガウスの発散定理を用いて式変形する方針が見えますね.
偏微分方程式の保存量の証明
偏微分方程式の解に関する何らかの積分$I(t)$が保存量または単調であることを示す際は,$I'(t)$について微分と積分の順序交換を行い,与えられた微分方程式を用いて$I'(t)$を変形するのが基本的な手法です.
たとえば,本問(1)と(2)では微分方程式より$u_t=\Delta{u}$であることを用いて
\begin{align*}M'(t)=\int_{\Omega}u_t(x,t)\,dx=\int_{\Omega}\Delta{u}(x,t)\,dx,
E'(t)=2\int_{\Omega}u(x,t)u_t(x,t)\,dx=2\int_{\Omega}u(x,t)\Delta{u}(x,t)\,dx\end{align*}
が得られます.ここで,被積分関数に$\Delta{u}$があるのでガウスの発散定理と境界条件を使って,整理する方針が見えます.
ガウスの発散定理
ガウスの発散定理は
- ベクトル場$\m{F}$の領域$\Omega$での湧き出し$\nabla\cdot\m{F}$の総量
- $\m{F}$の境界$\partial\Omega$からの漏れ出し$\m{F}(x)\cdot\m{n}(x)$の総量
が等しいという非常に直観的な定理ですね.
[ガウスの発散定理]$C^1$級の境界をもつ有界領域$\Omega\subset\R^d$と,$\Omega$の閉包$\overline{\Omega}$上の$C^1$級関数$\m{F}:\R^d\to\R^d$に対して,
\begin{align*}\int_{\Omega}\nabla\cdot\m{F}(x)\,dx=\int_{\partial\Omega}\m{F}(x)\cdot\m{n}(x)\,dS\end{align*}
が成り立つ.ただし,$\m{n}(x)$は$x\in\partial\Omega$での外向き単位法線ベクトルである.
とくに$\Delta{u}=\nabla\cdot\nabla{u}$とみてガウスの発散定理を用いるのは常套手段で,$M'(t)$は
\begin{align*}M'(t)=\int_{\Omega}\nabla\cdot\nabla{u}(x,t)\,dx=\int_{\partial\Omega}\nabla{u}(x,t)\cdot\nu(x)\,dS\end{align*}
となります.$\nabla{u}\cdot\nu=\frac{\partial u}{\partial \nu}$ですから,境界条件と併せて$M'(t)=0$が得られます.
また,積の微分公式$u\Delta{u}=\nabla\cdot(u\nabla{u})-\nabla{u}\cdot\nabla{u}$を使えば$E'(t)$でもガウスの発散定理が使えますね.
微分と積分の順序交換
$M'(t)$と$E'(t)$を求める際の微分と積分の順序交換を用いますが,微分と積分の順序交換を正当化するには次の定理を用いるのが常套手段です.
[微分と積分の順序交換条件]$A$を可測集合,$I$を開区間とする.$A\times I$上の可測関数$f(x,t)$は$t$について偏微分可能で,任意の$t\in I$に対して$f(\cdot,t)$は可積分であるとする.このとき,($t$によらない)ある$A$上の関数$g$が存在して,
- 任意の$t\in I$に対して$\abs{\frac{\partial f}{\partial t}(x,t)}\le g(x)$ a.e. $x\in A$
- $g$は$A$上可積分:$\int_{A}g(x)\,dx<\infty$
を満たすなら,
\begin{align*}\frac{d}{dt}\int_{A}f(x,t)\,dx=\int_{A}\frac{\partial f}{\partial t}(x,t)\,dx\end{align*}
が成り立つ.
この定理を使う際のポイントは
- (ほとんど至るところ)$|\frac{\partial f}{\partial t}(x,t)|\le g(x)$を満たす関数$g$をとる
- $\int_{A}g(x)\,dx<\infty$を満たす
の2つを示すことですね.証明は平均値の定理とルベーグの収束定理を用います.詳しくは以下の記事を参照してください.
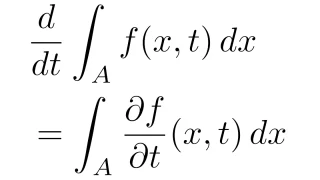
解答例
まずは全ての微分と積分の順序交換可能であるとして形式的に示し,最後に用いた微分と積分の順序交換を正当化する.また,積分$\int_{\Omega}f(x,t)\,dx$を$\int_{\Omega}f$と略記する.
(1)の解答
微分方程式より$u_t=\Delta{u}$が得られるので,任意の$t\in(0,\infty)$に対して
\begin{align*}M'(t)&=\int_{\Omega}u_t=\int_{\Omega}\Delta{u}=\int_{\Omega}\nabla\cdot\nabla{u}\end{align*}
であり,これはガウスの発散定理と境界条件より
\begin{align*}M'(t)&=\int_{\partial\Omega}\nabla{u}(x,t)\cdot\nu(x)\,dS=\int_{\partial\Omega}0\,dS=0\end{align*}
となる.よって,$M'(t)=0$が得られ,$M(t)$は$t$によらない定数関数である.
(2)の解答
微分方程式より$u_t=\Delta{u}$が得られるので,任意の$t\in(0,\infty)$に対して
\begin{align*}E'(t)&=\int_{\Omega}(u^2)_t=2\int_{\Omega}uu_t=2\int_{\Omega}u\Delta{u}
\\&=2\int_{\Omega}\nabla\cdot(u\nabla{u})-2\int_{\Omega}|\nabla{u}|^2\end{align*}
であり,この第1項はガウスの発散定理と境界条件より
\begin{align*}2\int_{\Omega}\nabla\cdot(u\nabla{u})
&=2\int_{\partial\Omega}(u(x,t)\nabla{u}(x,t))\cdot\nu(x)\,dS
\\&=2\int_{\partial\Omega}0\,dS=0\end{align*}
だから,$E'(t)=-2\int_{\Omega}|\nabla{u}|^2\le0$が従う.
(3)の解答
$\int_{\Omega}u(x,0)\,dx\neq0$と(1)より,任意の$t\in(0,\infty)$に対して$u(x,t)\not\equiv0$だから$E(t)>0$なので$H(t)$が定義される.任意の$t\in(0,\infty)$に対して,
\begin{align*}H^{\prime\prime}(t)=\frac{E^{\prime\prime}(t)E(t)-E'(t)^2}{E(t)^2}\end{align*}
だから,$E'(t)^2\le E^{\prime\prime}(t)E(t)$を示せばよい.$u\in C^{\infty}(\Omega\times(0,\infty))$より$u$の偏導関数は偏微分の順によらないから,微分方程式の両辺を微分して$(\nabla{u})_t=\nabla{\Delta{u}}$が得られるので,
\begin{align*}E^{\prime\prime}(t)&=-2\int_{\Omega}(|\nabla{u}|^2)_t=-4\int_{\Omega}\nabla{u}\cdot\nabla{u}_t
\\&=-4\int_{\Omega}\nabla{u}\cdot(\nabla{u})_t=-4\int_{\Omega}\nabla{u}\cdot\nabla{\Delta{u}}
\\&=-4\int_{\Omega}\nabla\cdot(\nabla{u}\Delta{u})+4\int_{\Omega}|\Delta{u}|^2\end{align*}
であり,この第1項はガウスの発散定理と境界条件より
\begin{align*}-4\int_{\Omega}\nabla\cdot(\nabla{u}\Delta{u})
=-4\int_{\partial\Omega}(\nabla{u}(x,t)\Delta{u}(x,t))\cdot\nu(x)\,dS=0\end{align*}
だから,$E^{\prime\prime}(t)=4\int_{\Omega}|\Delta{u}|^2$である.
また,ガウスの発散定理と境界条件とコーシー-シュワルツの不等式より
\begin{align*}\int_{\Omega}|\nabla{u}|^2&=\int_{\Omega}\nabla\cdot(u\nabla{u})-\int_{\Omega}u\nabla\cdot\nabla{u}
\\&=\int_{\partial\Omega}(u(x,t)\nabla{u}(x,t))\cdot\nu(x)\,dS-\int_{\Omega}u\Delta{u}
\\&\le\abs{\int_{\Omega}u\Delta{u}}
\le\bra{\int_{\Omega}|u|^2}^{1/2}\bra{\int_{\Omega}|\Delta{u}|^2}^{1/2}\end{align*}
が成り立つ.よって,両辺2乗して4倍すれば$E'(t)^2\le E^{\prime\prime}(t)E(t)$が成り立ち,$H^{\prime\prime}(t)\ge0$が従う.
(4)の解答
$H$は下に凸であり,0と$T$の$\frac{t}{T}:(1-\frac{t}{T})$内分点は
\begin{align*}0\cdot\bra{1-\frac{t}{T}}+T\cdot\frac{t}{T}=t\end{align*}
だから,$H(t)\le(1-\frac{t}{T})H(0)+\frac{t}{T}H(T)$が成り立つ.$H(t)=\log{E(t)}$を代入して
\begin{align*}&\log{E(t)}\le(1-\frac{t}{T})\log{E(0)}+\frac{t}{T}\log{E(T)}
\\&\iff E(t)\le E(0)^{1-\frac{t}{T}}E(T)^{\frac{t}{T}}\end{align*}
が成り立つ.
微分と積分の順序交換の正当化
任意に$\delta\in(0,1)$をとる.$u\in C^{\infty}(\Omega\times(0,\infty))$より,有界閉集合$\overline{\Omega}\times[\delta,\frac{1}{\delta}]$上で$u$と$u$の全ての偏導関数は連続だから有界なので,$u_t$, $(|u|^2)_t$, $(|u|^2)_{tt}$は有界である.
よって,平均値の定理とルベーグの収束定理より,任意の$t\in[\delta,\frac{1}{\delta}]$上で
\begin{align*}&M'(t)=\frac{d}{dt}\int_{\Omega}u=\int_{\Omega}u_t,
\\&E'(t)=\frac{d}{dt}\int_{\Omega}|u|^2=\int_{\Omega}(|u|^2)_t
\\&E”(t)=\frac{d}{dt}\int_{\Omega}(|u|^2)_t=\int_{\Omega}(|u|^2)_{tt}\end{align*}
が成り立つ.$\delta>0$の任意性より,$t\in(0,\infty)$上でもこの微分と積分の順序交換が成り立つ.
参考文献
以下,私も使ったオススメの入試問題集を挙げておきます.
詳解と演習大学院入試問題〈数学〉
[海老原円,太田雅人 共著/数理工学社]
理工系の修士課程への大学院入試問題集ですが,基礎〜標準的な問題が広く大学での数学の基礎が復習できる総合問題集として利用することができます.
実際,まえがきにも「単なる入試問題の解説にとどまらず,それを通じて,数学に関する読者の素養の質を高めることにある」と書かれているように,必ずしも大学院入試を受験しない一般の学習者にとっても学びやすい問題集です.また,構成が読みやすいのも個人的には嬉しいポイントです.
第1章 数え上げと整数
第2章 線形代数
第3章 微積分
第4章 微分方程式
第5章 複素解析
第6章 ベクトル解析
第7章 ラプラス変換
第8章 フーリエ変換
第9章 確率
一方で,問題数はそれほど多くないので,多くの問題を解きたい方には次の問題集もオススメです.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの問題集|詳解と演習 大学院入試問題(数理工学社)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.
演習 大学院入試問題
[姫野俊一,陳啓浩 共著/サイエンス社]
上記の問題集とは対称的に問題数が多く,まえがきに「修士の基礎数学の問題の範囲は,ほぼ本書中に網羅されている」と書かれているように,広い分野から問題が豊富に掲載されています.
全2巻で,
1巻第1編 線形代数
1巻第2編 微分・積分学
1巻第3編 微分方程式
2巻第4編 ラプラス変換,フーリエ変換,特殊関数,変分法
2巻第5編 複素関数論
2巻第6編 確率・統計
が扱われています.
地道にきちんと地に足つけた考え方で解ける問題が多く,確かな「腕力」がつくテキストです.入試では基本問題は確実に解けることが大切なので,その意味で試験への対応力が養われると思います.
なお,私自身は受験生時代に計算力があまり高くなかったので,この本の問題で訓練したのを覚えています.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの問題集|演習 大学院入試問題[数学](サイエンス社)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.




コメント