2022年度の京都大学 理学研究科 数学・数理解析専攻 数学系の大学院入試問題の「基礎科目」の解答の方針と解答です.
問題は6問あり,全6問を解答します.試験時間は3時間30分です.この記事では,全6問の考え方と解答例を掲載しています.
ただし,公式に採点基準などは発表されていないため,本稿の解答が必ずしも正解になるとは限りません.ご注意ください.
また,十分注意して解答を作成していますが,論理の飛躍・誤りが残っている場合があります.
なお,過去問は京都大学の数学教室の過去問題のページから入手できます.
第1問(微分積分学)
次の広義積分が収束するような実数$a$の範囲を求めよ.
\begin{align*}\iint_{D}\frac{y}{(1+\sqrt{x^2+y^2}-x)^2(x^2+y^2)^\alpha}\,dxdy\end{align*}
ただし,$D=\set{(x,y)\in\R^2}{x\ge0,y\ge0,x^2+y^2\ge1}$とする.
広義積分の重積分が収束するための必要十分条件を求める問題です.
解答の方針とポイント
積分領域$D$が非有界なので広義重積分です.また,問題文に$x^2+y^2$が3箇所も現れるので極座標変換$(x,y)=(r\cos{\theta},r\sin{\theta})$が使えそうですね.
重積分の広義積分
非負実数値多変数関数の重積分の広義積分は,有界閉集合上で通常の重積分を計算したものの極限(または上限)により定義されます.
非負実数値$n$変数関数$f$と,体積確定集合$D\subset\R^n$を考える.さらに
\begin{align*}D_n\subset D_{n+1},\quad D=\bigcup_{n=1}^{\infty}D_n\end{align*}
を満たす体積確定な有界閉集合の列$\{D_n\}$をとる.任意の$n$に対して$f$が$D_n$上可積分であれば
\begin{align*}\int_{D}f(x)\,dx=\lim_{n\to\infty}\int_{D_n}f(x)\,dx\end{align*}
を$f$の$D$上の広義積分という.
$f$が非負であることから,この$f$の$D$上の広義積分は列$\{D_n\}$のとりかたによらないことが従います.
ざっくり言えば,どんどん集合$D$に近付く有界閉集合上で$f$が可積分なら,その極限を$A$上での広義積分と定義するわけですね.
このあたりの考え方は1次元の広義積分と同様ですね.
極座標変換と相性の良い積分領域
原点中心の扇形は極座標変換$(r,\theta)\mapsto(x,y)=(r\cos{\theta},r\sin{\theta})$と相性が良いので,$D$を近似する有界閉集合$D_n$をたとえば
\begin{align*}D_n=\set{(x,y)\in D}{1\le x^2+y^2\le n^2}\end{align*}
ととると良さそうです.
実際,このとき極座標変換$(r,\theta)\mapsto(x,y)$で$D_n$に対応する領域は$[1,n]\times[0,\frac{\pi}{2}]$となるので,問題の積分は
\begin{align*}\int_{1}^{n}\bra{\int_{0}^{\frac{\pi}{2}}\frac{r\cdot r\sin{\theta}}{(1+r-r\cos{\theta})^2r^{2\alpha}}\,d\theta}\,dr\end{align*}
と書き換えられますね.
分子の最初の$r$は2次元での極座標変換でのヤコビアンです.積分の変数変換ではヤコビアンを忘れないように注意しましょう.
1次元の広義積分$\int_{1}^{\infty}\frac{1}{x^p}\,dx$の収束条件
書き換えた積分はさらに$\int_{1}^{n}\frac{1}{(1+r)r^{2\alpha-2}}\,dr$と計算できるので,この積分が$n\to\infty$で収束する条件を求めれば良いことになります.$r$が十分大きいとき
\begin{align*}\frac{1}{(1+r)r^{2\alpha-2}}\approx\frac{1}{r^{2\alpha-1}}\end{align*}
ですから,求める$\alpha$の条件は広義積分
\begin{align*}\int_{1}^{\infty}\frac{1}{r^{2\alpha-1}}\,dr\end{align*}
が収束するための条件と同じですね.この条件は計算しても得られますが,広義積分$\int_{1}^{\infty}\frac{1}{x^p}\,dx$が収束するための$p\in\R$の必要十分条件は当たり前にしておきましょう.
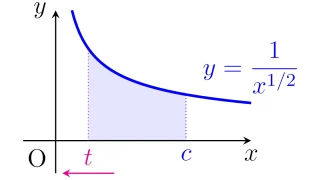
$c>0$とする.$p\in\R$に対して,次が成り立つ.
\begin{align*}\int_{c}^{\infty}\frac{1}{x^p}\,dx=\begin{cases}\infty,&p\le1\\\dfrac{c^{1-p}}{p-1},&p>1.\end{cases}\end{align*}
遠方$x\to\infty$で関数が十分減衰しないと$[1,\infty)$での$\frac{1}{x^p}$の広義積分は収束しません.その収束・発散の境目が$p=1$になっているというわけですね.
解答例
$n\in\N$に対して$D_n:=\set{(x,y)\in D}{x^2+y^2\le n^2}$とおくと,$\{D_n\}$は
\begin{align*}D_n\subset D_{n+1},\quad D=\bigcup_{n=1}^{\infty}D_n\end{align*}
を満たす面積確定な有界閉集合の列である.問題の広義積分の被積分関数は$D$上で非負だから
\begin{align*}I_n:=\iint_{D_n}\frac{y}{(1+\sqrt{x^2+y^2}-x)^2(x^2+y^2)^\alpha}\,dxdy\end{align*}
とおくと,求める広義積分は$\lim\limits_{n\to\infty}I_n$である.
各$D_n$上で極座標変換$(r,\theta)\mapsto(x,y)=(r\cos\theta,r\sin\theta)$を施すと,$D_n$は縦線集合$[1,n]\times[0,\frac{\pi}{2}]$に対応し,ヤコビ行列式は$\det{\frac{\partial(x,y)}{\partial(r,\theta)}}=r$である.よって,
\begin{align*}I_n&=\int_{[1,n]\times[0,\frac{\pi}{2}]}\frac{r\cdot r\sin{\theta}}{(1+r-r\cos{\theta})^2r^{2\alpha}}\,drd\theta
\\&=\int_{1}^{n}\frac{1}{r^{2\alpha-2}}\bra{\int_{0}^{\frac{\pi}{2}}\frac{\sin{\theta}}{(1+r-r\cos{\theta})^2}\,d\theta}\,dr
\\&=\int_{1}^{n}\frac{1}{r^{2\alpha-2}}\bra{-\frac{1}{r}\brc{\frac{1}{1+r-r\cos{\theta}}}_{0}^{\frac{\pi}{2}}}\,dr
\\&=\int_{1}^{n}\frac{1}{(1+r)r^{2\alpha-2}}\,dr\end{align*}
である.$1\le r$のとき$\frac{1}{2r^{2\alpha-1}}\le\frac{1}{(1+r)r^{2\alpha-2}}<\frac{1}{r^{2\alpha-1}}$なので,$\lim\limits_{n\to\infty}I_n$が収束することと$\lim\limits_{n\to\infty}\int_{1}^{n}\frac{1}{r^{2\alpha-1}}\,dr$が収束することは必要十分である.すなわち,求める$\alpha$の条件は
\begin{align*}2\alpha-1>1\iff \alpha>1\end{align*}
である.
第2問(線形代数学)
$V$を実ベクトル空間とし,$v_1,v_2,v_3,v_4$を$V$の1次独立なベクトルとする.$a\in\R$に対し
\begin{align*}&w_1=v_1-v_2+v_3
\\&w_2=v_1+(a-1)v_2+v_3-av_4
\\&w_3=2v_1-2v_2+(a+2)v_3
\\&w_4=v_1-v_2+v_3+(a+1)v_4\end{align*}
とおく.
- $w_1,w_2,w_3,w_4$が1次独立となるような$a$の条件を求めよ.
- $w_1,w_2,w_3,w_4$が1次従属となる$a$に対し,$w_1,w_2,w_3,w_4$で生成される$V$の部分空間$\anb{w_1,w_2,w_3,w_4}$の次元を求めよ.
ほとんどの$a$で線形独立(1次独立)となりますが,一部の$a$で線形従属(1次従属)なのでその場合に$w_1,w_2,w_3,w_4$が張る部分空間の次元を求める問題です.
解答の方針とポイント
$w_1,w_2,w_3,w_4$が$v_1,v_2,v_3,v_4$の線形結合で表されているので,
\begin{align*}[w_1,w_2,w_3,w_4]=[v_1,v_2,v_3,v_4]\bmat{1&1&2&1\\-1&a-1&-2&-1\\1&1&a+2&1\\0&-a&0&a+1}\end{align*}
と表せます.$v_1,v_2,v_3,v_4$が線形独立ですから,$w_1,w_2,w_3,w_4$が線形独立であることと行列$\sbmat{1&1&2&1\\-1&a-1&-2&-1\\1&1&a+2&1\\0&-a&0&a+1}$のランクが4であることと同値ですね.
行列$\sbmat{1&1&2&1\\-1&a-1&-2&-1\\1&1&a+2&1\\0&-a&0&a+1}$は正方行列なので,この行列が正則行列であることとも同値ですね.
また,(2)で求める$w_1,w_2,w_3,w_4$で生成される$V$の部分空間$\anb{w_1,w_2,w_3,w_4}$の次元は,$w_1,w_2,w_3,w_4$のうちの線形独立なものの最大個数なので,(1)と同様に行列$\sbmat{1&1&2&1\\-1&a-1&-2&-1\\1&1&a+2&1\\0&-a&0&a+1}$のランクを求めれば良いですね.
解答例
$A:=\sbmat{1&1&2&1\\-1&a-1&-2&-1\\1&1&a+2&1\\0&-a&0&a+1}$とおくと,$w_1,w_2,w_3,w_4$の定義から
\begin{align*}&[w_1,w_2,w_3,w_4]=[v_1,v_2,v_3,v_4]A\end{align*}
と表せる.
(1)の解答
$k_1,k_2,k_3,k_4\in\R$が$\sum\limits_{i=1}^{4}k_iw_i=\m{0}_V$を満たすとする.左辺は
\begin{align*}\sum_{i=1}^{4}k_iw_i=[w_1,w_2,w_3,w_4]\bmat{k_1\\k_2\\k_3\\k_4}=[v_1,v_2,v_3,v_4]A\bmat{k_1\\k_2\\k_3\\k_4}\end{align*}
となるので,$v_1,v_2,v_3,v_4$が1次独立であることから
\begin{align*}A\bmat{k_1\\k_2\\k_3\\k_4}=\bmat{0\\0\\0\\0}\end{align*}
が成り立つ.よって,$w_1,w_2,w_3,w_4$が1次独立であることと,正方行列$A$のランクが4であることは同値である.
\begin{align*}\rank{A}=\rank{\bmat{1&1&2&1\\0&a&0&0\\0&0&a&0\\0&-a&0&a+1}}
=\rank{\bmat{1&1&2&1\\0&a&0&0\\0&0&a&0\\0&0&0&a+1}}\end{align*}
だから,求める$a$の条件は$\rank{A}=4\iff a\neq0,-1$である.
(2)の解答
(1)より$w_1,w_2,w_3,w_4$が1次従属となる$a$は$a=0,-1$である.$V$の部分空間$\anb{w_1,w_2,w_3,w_4}$の次元は$w_1,w_2,w_3,w_4$のうち線形独立なものの最大個数であり,これは(1)と同様に$\rank{A}$に等しい.よって,
\begin{align*}\dim{\anb{w_1,w_2,w_3,w_4}}
&=\rank{\bmat{1&1&2&1\\0&a&0&0\\0&0&a&0\\0&0&0&a+1}}
\\&=\begin{cases}2,&a=0,\\3,&a=-1\end{cases}\end{align*}
である.
第3問(群論)
アーベル群$G=\Z/2\Z\times\Z/3\Z\times\Z/3\Z\times\Z/4\Z$の部分群$H$を$H=\set{(a,b,0,0)}{a\in\Z/2\Z,b\in\Z/3\Z}$とするとき,$G$の位数12の部分群$K$で$G=K+H$となるものの数を求めよ.ただし
\begin{align*}K+H=\set{\alpha+\beta}{\alpha\in K,\beta\in H}\end{align*}
である.
群$G$の部分群$H$に対する補群($G=H+K$かつ$H\cap K=\{e\}$を満たす部分群$K$)の個数を求める問題です.
解答の方針とポイント
$H$で第1成分と第2成分の全ての組を全て作れますが,第3成分と第4成分は$(0,0)$しか作れません.よって,$K$で$(*,*,c,d)$($c=0,1,2$, $d=0,1,2,3$)なる元を全て作ればよいですね($*$は任意の成分).
$|K|=12$ですから,どの組$(c,d)$に対しても$(*,*,c,d)$の形の$K$の元は1つずつしかないことになります.
よって,たとえば$K=\anb{(0,0,1,0),(0,0,0,1)}$とすると$G=K+H$が成り立つことが分かります.他にも$K=\anb{(1,0,1,0),(0,0,0,1)}$のように,生成元の第1成分と第2成分が0でなくても$G=K+H$となりますね.
本質的には同じことですが,中国式剰余定理より同型$G\cong\Z/6\Z\times\Z/12\Z$を考えて,$\Z/6\Z\times\Z/12\Z$で議論する方が分かりやすく解答も書きやすいでしょう.
解答例
中国式剰余定理より,写像
\begin{align*}G\to G’:=\Z/6\Z\times\Z/12\Z;(a,b,c,d)\mapsto(x,y)\end{align*}
は同型である.ただし,$x\equiv a\pmod{2}$, $x\equiv b\pmod{3}$, $y\equiv c\pmod{3}$, $y\equiv d\pmod{4}$である.
また,この同型で$H$は
\begin{align*}H\to H’:=\Z/6\Z\times\{0\}\end{align*}
に対応するから,$G’$の位数12の部分群$K’$で$G’=K’+H’$となるものの数を求めればよい.
$H’$のすべての元の第2成分が0だから,$|K’|=12$に注意すると$K’$は第2成分が$0,1,2,\dots,11$の元を1個ずつもつ.よって,ある$p\in\Z/6\Z$がただひとつ存在して$(p,1)\in K’$となるので,$K’=\anb{(p,1)}$である.
$p=0,1,2,3,4,5$ですべて異なる$K’$となるので,条件を満たす部分群$K$は6個である.
第4問(微分積分学)
$\R$で定義された関数
\begin{align*}f(x)=\int_{0}^{\infty}|x+t\sin{t}|e^{-t}\,dt\end{align*}
は最小値を持つことを示せ.
積分で表された関数が最小値をもつことを示す問題です.
解答の方針とポイント
被積分関数は$t\to\infty$で指数減衰するので,積分は$t\approx0$での寄与がほとんどであることがポイントです.
コンパクト集合上の連続関数は最大値・最小値をもつ
関数が最大値・最小値をもつことを保証する定理として,次の定理は重要ですね.
コンパクト集合$X$に対して,関数$f:X\to\R$を考える.$f$が連続なら,$f$は$X$上で最大値・最小値をとる.
直観的には,$t\approx0$のとき$|x+t\sin{t}|e^{-t}\approx|x|$なので,$|x|$が大きければ$f(x)$の積分が大きくなり$f(x)$は大きな値をとりそうです.よって,ある$R>0$が存在して,$\R\setminus[-R,R]$上では一定以上の値を取り最小値をとらないことを示せそうですね.
これを示すことができば,あとは$f$が連続であることを示せばよいですね.
$|x|$がある程度大きいと$f(x)$も大きい
上の議論から,$f$が最小値をもつなら,$x$が0に近いところで最小値をとりそうです.たとえば,$x=0$のときは
\begin{align*}f(0)=\int_{0}^{\infty}t|\sin{t}|e^{-t}\,dt\le1\end{align*}
と評価できるので,少なくとも$f(x)$の最小値は(存在すれば)1以下であることが分かります.また,$|x|\ge1$なら
\begin{align*}f(x)=\int_{0}^{1}(|x|-|t\sin{t}|)e^{-t}\,dt\ge(|x|-1)(1-e^{-1})\end{align*}
となるので,$|x|$が十分大きければ$f(x)\ge1$となることが分かり,ある$R>0$が存在して$\R\setminus[-R,R]$上で$f$は最小値をとらないことが分かりますね.
解答例
$f$の定義より
\begin{align*}f(0)=\int_{0}^{\infty}|t\sin{t}|e^{-t}\,dt\le\int_{0}^{\infty}te^{-t}\,dt=1\end{align*}
である.また,任意の$x\in\R\setminus[-3,3]$に対して,
\begin{align*}f(x)&\ge\int_{0}^{1}|x+t\sin{t}|e^{-t}\,dt\ge\int_{0}^{1}(|x|-|t\sin{t}|)e^{-t}\,dt
\\&\ge\int_{0}^{1}(|x|-1)e^{-t}\,dt=(|x|-1)(1-e^{-1})
\\&>(3-1)(1-2^{-1})=1\end{align*}
である.よって,$f$は$\R\setminus[-3,3]$上で最小値をとることはない.
さらに,任意の$x\in\R$と任意の$h\in\R\setminus\{0\}$に対して,
\begin{align*}|f(x+h)-f(x)|&=\abs{\int_{0}^{\infty}(|(x+h)+t\sin{t}|-|x+t\sin{t}|)e^{-t}\,dt}
\\&\le\int_{0}^{\infty}\bigl||(x+h)+t\sin{t}|-|x+t\sin{t}|\bigr|e^{-t}\,dt
\\&\le\abs{\int_{0}^{\infty}|h|e^{-t}\,dt}=|h|\end{align*}
なので,$\lim_{h\to0}|f(x+h)-f(x)|=0$となって$f$は$\R$上連続である.よって,有界閉(コンパクト)集合上の連続関数は最小値をもつから,$f$は$[-3,3]$上に最小値をもち,$f$は$\R$上で最小値をもつ.
第5問(複素解析学)
次の広義積分を求めよ.
\begin{align*}\int_{-\infty}^{\infty}\frac{x^3\sin{x}}{(x^2+1)^2}\,dx.\end{align*}
典型的な留数定理の広義積分の計算への応用ですね.
解答の方針とポイント
「もとの広義積分を実軸上の区間$L_R$上の複素積分で表し,閉曲線$C_R\cup L_R$上の複素積分を留数定理で求め,余分な$C_R$上の複素積分が$R\to\infty$で0に収束することを示す」という基本的な議論で解けます.
広義積分と複素積分と留数定理
計算する広義積分は
\begin{align*}&f(z)=\frac{z^3e^{iz}}{(z^2+1)^2},
\\&L_R=\set{z\in\C}{z=x,x\in[-R,R]}\end{align*}
とおくことで,複素積分で$\lim\limits_{R\to\infty}\operatorname{Im}\int_{L_R}f(z)\,dz$と表せますね.
また,$(z^2+1)^2=(z+i)^2(z-i)^2$なので,$f$の極は$\pm i$でいずれも2位の極ですから,
\begin{align*}C_R:=\set{z\in\C}{z=Re^{i\theta},\theta\in[0,\pi]}\end{align*}
とすれば,$R>1$のときは$C_R\cup L_R$上で$f$は連続で,$i$を除く$C_R\cup L_R$の内部で$f$は正則です.
よって,留数定理より,任意の$R>1$に対して
\begin{align*}\int_{C_R\cup L_R}f(z)\,dz=2\pi i\mathrm{Res}(f,i)\end{align*}
が成り立ちますから,あとは留数$\mathrm{Res}(f,i)$を求め,$\lim\limits_{R\to\infty}\int_{C_R}f(z)\,dz=0$を示せばよいですね.
留数$\mathrm{Res}(f,i)$の求め方
基本的には,複素関数$f$が点$\alpha$に$m$位の極をもつときは,$f$のローラン展開
\begin{align*}f(z)=\sum_{n=-m}^{\infty}a_n(z-\alpha)^n\end{align*}
を考えて,
\begin{align*}\mathrm{Res}(f,\alpha)=\lim_{z\to\alpha}\frac{1}{(m-1)!}\frac{d^{m-1}}{dz^{m-1}}\bra{(z-\alpha)^mf(z)}\end{align*}
と留数が求められます.本問題では,$i$は$f$の2位の極なので$\alpha=i$, $m=2$の場合で考えればよいですね.
上半円$C_R$上の複素積分は$R\to\infty$で0に収束する
$R>1$とします.上半円$C_R$上の$f$の複素積分は,$C_R$の長さが$\pi R$であることから
\begin{align*}\abs{\int_{C_R}f(z)\,dz}\approx\pi R\cdot|f(Re^{i\theta})|=\frac{\pi R^4e^{-R\sin{\theta}}}{(R^2-1)^2}\end{align*}
と大雑把に見積もることができます($\theta\in[0,\pi]$).$\frac{R^4}{(R^2-1)^2}\xrightarrow[]{R\to\infty}1$であり,$\theta$によらず$e^{-R\sin{\theta}}\xrightarrow[]{R\to\infty}0$なので,$\lim\limits_{R\to\infty}\int_{C_R}f(z)\,dz=0$となりそうですね.
以上の議論を厳密にするには,$z=Re^{it}$と変数変換して
\begin{align*}\abs{\int_{C_R}f(z)\,dz}&=\abs{\int_{0}^{\pi}f(Re^{it})\bra{iRe^{it}\,dt}}
\\&\le\frac{R^4}{(R^2-1)^2}\int_{0}^{\pi}e^{-R\sin{t}}\,dt\end{align*}
と評価して,$\lim\limits_{R\to\infty}\int_{0}^{\pi}e^{-R\sin{t}}\,dt=0$を示せばよいですね.$e^{-R\sin{t}}$を直接積分するのは難しいですが,こういう場合はジョルダンの不等式
\begin{align*}\frac{2}{\pi}t\le\sin{t}\quad\bra{t\in\brc{0,\frac{\pi}{2}}}\end{align*}
を用いて
\begin{align*}\int_{0}^{\pi}e^{-R\sin{t}}\,dt\le2\int_{0}^{\pi/2}e^{-2Rt/\pi}\,dt\xrightarrow[]{R\to\infty}0\end{align*}
と示すのが常套手段ですね.
解答例
領域$\C\setminus\{\pm i\}$上の正則関数$f$を
\begin{align*}f(z)=\frac{z^3e^{iz}}{(z^2+1)^2}\end{align*}
で定める.また,$R>1$に対して閉曲線$\Gamma_R\subset\C\setminus\{\pm i\}$を
\begin{align*}&L_R:=\set{z\in\C}{z=x,x\in[-R,R]},
\\&C_R:=\set{z\in\C}{z=Re^{it},t\in[0,\pi]},
\\&\Gamma_R:=L_R\cup C_R\end{align*}
で定める.ただし,閉曲線$\Gamma_R$の向きは正方向(内部を左側に見ながら回る向き)とする.
このとき,求める広義積分を$I$とおくと,
\begin{align*}I&=\lim_{R\to\infty}\int_{-R}^{R}\frac{x^3\sin{x}}{(x^2+1)^2}\,dx
\\&=\lim_{R\to\infty}\operatorname{Im}\int_{-R}^{R}\frac{x^3e^{ix}}{(x^2+1)^2}\,dx
\\&=\lim_{R\to\infty}\operatorname{Im}\int_{L_R}f(z)\,dz\end{align*}
である.ただし,$z\in\C$に対して$\operatorname{Im}z$は$z$の虚部を表す.
[1]閉曲線$\Gamma_R$の内部に存在する$f$の極は$i$で,$i$は$f$の2位の極である.よって,
\begin{align*}g(z)=(z-i)^2f(z)=\frac{z^3e^{iz}}{(z+i)^2}\end{align*}
で複素関数$g$を定めると,留数定理より
\begin{align*}\int_{\Gamma_R}f(z)\,dz
&=2\pi i\operatorname{Res}(f,i)
=\lim_{z\to i}2\pi i\cdot\frac{1}{1!}\od{g}{z}(z)
\\&=\lim_{z\to i}2\pi i\bra{\frac{-2z^3e^{iz}}{(z+i)^3}+\frac{3z^2e^{iz}+iz^3e^{iz}}{(z+i)^2}}
\\&=2\pi i\bra{\frac{-2i^3e^{i^2}}{8i^3}+\frac{3i^2e^{i^2}+i^4e^{i^2}}{4i^2}}
\\&=2\pi i\bra{-\frac{1}{4e}+\frac{1}{2e}}=\frac{\pi i}{2e}\end{align*}
を得る.
[2]$z\in C_R$は$z=R(\cos{t}+i\sin{t})$($t\in[0,\pi]$)と表せるので,
\begin{align*}|e^{iz}|=\abs{e^{R(i\cos{t}-\sin{t})}}=e^{-R\sin{t}}\end{align*}
であることに注意すると,三角不等式と併せて
\begin{align*}\abs{\int_{C_R}f(z)\,dz}
&\le\abs{\int_{0}^{\pi}\frac{z^3e^{iz}}{(z^2+1)^2}\,Rie^{it}dt}
\\&\le\int_{0}^{\pi}\frac{R^4e^{-R\sin{t}}}{(R^2-1)^2}\,dt
\\&=\frac{2R^4}{(R^2-1)^2}\int_{0}^{\pi/2}e^{-R\sin{t}}\,dt
\\&\le\frac{2R^4}{(R^2-1)^2}\int_{0}^{\pi/2}e^{-2Rt/\pi}\,dt
\\&\le\frac{\pi R^3}{(R^2-1)^2}(1-e^{-R})
\xrightarrow[]{R\to\infty}0\end{align*}
なので,$\lim_{R\to\infty}\abs{\int_{C_R}f(z)\,dz}=0$が成り立つ.
以上より,求める広義積分$I$は
\begin{align*}I&=\lim_{R\to\infty}\operatorname{Im}\bra{\int_{\Gamma_R}f(z)\,dz-\int_{C_R}f(z)\,dz}
\\&=\operatorname{Im}\bra{\frac{\pi i}{2e}-0}=\frac{\pi}{2e}\end{align*}
である.
第6問(微分幾何学)
ユークリッド空間$\R^4$の部分空間$X$を
\begin{align*}X=\set{(x,y,z,w)\in\R^4}{x^2+y^2+z^2+w^2=1,x^3+y^3+z^3+w^3=0}\end{align*}
で定める.このとき$X$はコンパクトな微分可能多様体であることを示せ.
与えられた集合が部分多様体であることを示す問題です.
解答の方針とポイント
微分可能部分多様体であることを示す方法としては正則値定理(沈め込み定理)が重要です.
微分可能多様体$M$, $N$と,写像$f:M\to N$に対して,$p\in M$が$f$の正則点であるとは微分$(df)_p:T_p(M)\to T_f(p)(N)$が全射であることをいい,正則点でない$M$上の点は臨界点というのでした.
$p\in M$が$f$の正則点であることと,$\rank{Jf(p)}=\dim{N}$が成り立つことと同値なのでした($Jf(p)$は$f$の$p$におけるヤコビ行列).
さらに,臨界点の像を臨界値といい,臨界値でない$N$の元を正則値といいますね.
正則値の逆像が$\emptyset$または$M$上の微分可能部分多様体であることを述べた次の定理を正則値定理(沈め込み定理)といいます.
[正則値定理]$C^s$級微分可能多様体$M$, $N$と,$C^s$級写像$f:M\to N$に対して,$f$の正則値$q\in N$の逆像$f^{-1}(q)$は$M$の$(\dim{M}-\dim{N})$次元$C^s$級部分多様体である.
本問題では$f:\R^4\to\R^2$を
\begin{align*}f(x,y,z,w)=\bmat{x^{2}+y^{2}+z^{2}+w^{2}-1\\x^3+y^3+z^3+w^3}\end{align*}
で定義すると$X=f^{-1}(0,0)$となりますから,$(0,0)\in\R^2$が正則点であることを示せば,$f$に正則値定理(沈め込み定理)が適用できますね.
また,一般に$\R^n$の部分集合がコンパクトであることと有界閉であることは同値ですね(ハイネ-ボレルの定理).有界であることは$X$の条件から分かり,$f$は連続で1点集合$\{(0,0)\}$は閉なので$X=f^{-1}(0,0)$が閉であることも分かりますね.
解答例
写像$f:\R^4\to\R^2$を
\begin{align*}f(x,y,z,w)=\bmat{x^2+y^2+z^2+w^2-1\\x^3+y^3+z^3+w^3}\end{align*}
で定める.$X=f^{-1}(0,0)$であり,$(\frac{1}{2},-\frac{1}{2},\frac{1}{2},-\frac{1}{2})\in X$だから$X\neq\emptyset$である.
ここで,任意の$p:=(x,y,z,w)\in X$が$f$の正則点であることを示す.そのために,$\operatorname{rank}Jf_{p}\neq2$と仮定して矛盾を導く.このとき,
\begin{align*}Jf_{p}=\bmat{2x&2y&2z&2w\\3x^2&3y^2&3z^2&3w^2}\end{align*}
である.$x^2+y^2+z^2+w^2=1$より$(x^2,y^2,z^2,w^2)\neq(0,0,0,0)$だから,ある$k\in\R$が存在して
\begin{align*}(2x,2y,2z,2w)=k(3x^2,3y^2,3z^2,3w^2)\end{align*}
を満たす.よって,$p\in X$であることに注意して
\begin{align*}0&=3k(x^3+y^3+z^3+w^3)
\\&=x\cdot3kx^2+y\cdot3ky^2+z\cdot3kz^2+w\cdot3kw^2
\\&=x\cdot2x+y\cdot2y+z\cdot2z+w\cdot2w
\\&=2(x^2+y^2+z^2+w^2)=2\end{align*}
と矛盾を得る.よって,仮定は誤りで任意の$p\in X$が$f$の正則点なので,正則値定理より$X=f^{-1}(0,0)$は微分可能多様体である.
また,任意の$p:=(x,y,z,w)\in X$に対して$x^2+y^2+z^2+w^2=1<\infty$だから$X$は有界であり,$f$が連続で1点集合$\{(0,0)\}$は閉だから$f^{-1}(0,0)$も閉である.よって,$X$はコンパクトである.
参考文献
以下,私も使ったオススメの入試問題集を挙げておきます.
詳解と演習大学院入試問題〈数学〉
[海老原円,太田雅人 共著/数理工学社]
理工系の修士課程への大学院入試問題集ですが,基礎〜標準的な問題が広く大学での数学の基礎が復習できる総合問題集として利用することができます.
実際,まえがきにも「単なる入試問題の解説にとどまらず,それを通じて,数学に関する読者の素養の質を高めることにある」と書かれているように,必ずしも大学院入試を受験しない一般の学習者にとっても学びやすい問題集です.また,構成が読みやすいのも個人的には嬉しいポイントです.
第1章 数え上げと整数
第2章 線形代数
第3章 微積分
第4章 微分方程式
第5章 複素解析
第6章 ベクトル解析
第7章 ラプラス変換
第8章 フーリエ変換
第9章 確率
一方で,問題数はそれほど多くないので,多くの問題を解きたい方には次の問題集もオススメです.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの問題集|詳解と演習 大学院入試問題(数理工学社)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.
演習 大学院入試問題
[姫野俊一,陳啓浩 共著/サイエンス社]
上記の問題集とは対称的に問題数が多く,まえがきに「修士の基礎数学の問題の範囲は,ほぼ本書中に網羅されている」と書かれているように,広い分野から問題が豊富に掲載されています.
全2巻で,
1巻第1編 線形代数
1巻第2編 微分・積分学
1巻第3編 微分方程式
2巻第4編 ラプラス変換,フーリエ変換,特殊関数,変分法
2巻第5編 複素関数論
2巻第6編 確率・統計
が扱われています.
地道にきちんと地に足つけた考え方で解ける問題が多く,確かな「腕力」がつくテキストです.入試では基本問題は確実に解けることが大切なので,その意味で試験への対応力が養われると思います.
なお,私自身は受験生時代に計算力があまり高くなかったので,この本の問題で訓練したのを覚えています.
なお,本書については,以下の記事で書評としてまとめています.
【オススメの問題集|演習 大学院入試問題[数学](サイエンス社)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.




コメント