$n$次正方行列$A$に対して$AB=BA=I$を満たす正方行列$B$が存在するとき
- $A$を正則行列
- $B$を$A$の逆行列
といい，$B=A^{-1}$と表すのでした（$I$は単位行列）．
このように正則行列であることの定義式は$AB=BA=I$ですが，実は$AB=I$か$BA=I$の少なくとも一方が成り立てば正則行列となることが証明できます．
このことを証明するためには基本変形が行列の掛け算で表せることを理解しておきたいところです．
この記事では，正方行列$A$が正則であるためには$AB=I$か$BA=I$を満たす正方行列$B$が存在すれば良いことの証明を目標として
- 行基本変形の確認
- 基本変形を引き起こす行列
- 正則性の条件
を順に説明します．
なお，この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが，複素行列など一般の体を成分とする行列・ベクトルに対しても同様です．
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
線形代数学の参考文献
以下は線形代数学に関するオススメの教科書です．
大学教養 線形代数（加藤文元 著）
数学科など理論系の学生向けの線形代数の入門書です．平易な例から丁寧に説明されています．
手を動かしてまなぶ 線形代数（藤岡敦 著）
理論と演習のバランスをとりながら勉強したい人にオススメの入門書です．
行基本変形の確認
まずは行基本変形がどういうものだったか確認しておきましょう．
連立１次方程式$\begin{cases}2x+3y=8\\x+2y=5\end{cases}$は以下のように加減法により解くことができます：
\begin{align*}
\left\{\begin{matrix}
2x&+&3y&=&8\\
x&+&2y&=&5
\end{matrix}\right.
\iff&
\left\{\begin{matrix}
x&+&2y&=&5\\
2x&+&3y&=&8
\end{matrix}\right.
\\\iff&
\left\{\begin{matrix}
x&+&2y&=&5\\
&-&y&=&-2
\end{matrix}\right.
\\\iff&
\left\{\begin{matrix}
x&&&=&1\\
&-&y&=&-2
\end{matrix}\right.
\\\iff&
\left\{\begin{matrix}
x&&&=&1\\
&&y&=&2
\end{matrix}\right.
\end{align*}
連立１次方程式の加減法は係数と定数をいじっているだけなので，以下のように拡大係数行列$\bmat{2&3&8\\1&2&5}$の変形と対応しますね．
\begin{align*}
&\left\{\begin{matrix}
2x&+&3y&=&8\\
x&+&2y&=&5
\end{matrix}\right.
&\leftrightarrow&&\bmat{2&3&8\\1&2&5}
\\\iff&
\left\{\begin{matrix}
x&+&2y&=&5\\
2x&+&3y&=&8
\end{matrix}\right.
&\leftrightarrow&&\bmat{1&2&5\\2&3&8}
\\\iff&
\left\{\begin{matrix}
x&+&2y&=&5\\
&-&y&=&-2
\end{matrix}\right.
&\leftrightarrow&&\bmat{1&2&5\\0&-1&-2}
\\\iff&
\left\{\begin{matrix}
x&&&=&1\\
&-&y&=&-2
\end{matrix}\right.
&\leftrightarrow&&\bmat{1&0&1\\0&-1&-2}
\\\iff&\left\{\begin{matrix}
x&&&=&1\\
&&y&=&2
\end{matrix}\right.
&\leftrightarrow&&\bmat{1&0&1\\0&1&2}
\end{align*}
この連立１次方程式の加減法に対応する行列の変形を行基本変形というのでした．
行列について
- ある行と別の行を入れ替える
- ある行を$k$倍する($k\neq0$)
- ある行の$k$倍を別の行に加える
という３つの変形を併せて行基本変形という．
基本変形を引き起こす行列
連立１次方程式の加減法をもとに定義された行基本変形ですが，実は行列の掛け算をかけることで基本変形を引き起こすことができます．
基本変形
いま行基本変形の定義を述べましたが，行列の列に関しての同様の変形を列基本変形といいます．
行列について
- ある列と別の列を入れ替える
- ある列を$k$倍する($k\neq0$)
- ある列の$k$倍を別の列に加える
という３つの変形を併せて列基本変形という．
列基本変形の定義は，行基本変形の定義で「行」を「列」に読み替えただけですね．
列基本変形と行基本変形を併せて基本変形という．
基本変形を引き起こす行列
行列$A:=\bmat{1&2&3\\4&5&6\\7&8&9\\10&11&12}$と，以下の行列を考えます．
\begin{align*}P_{34}:=\bmat{1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0},\quad
Q_{2}^{(3)}:=\bmat{1&0&0&0\\0&3&0&0\\0&0&1&0\\0&0&0&1},\quad
R_{14}^{(2)}:=\bmat{1&0&0&2\\0&1&0&0\\0&0&1&0\\0&0&0&1}\end{align*}
このとき，定義通り計算すると
\begin{align*}P_{34}A=\bmat{1&2&3\\4&5&6\\10&11&12\\7&8&9},\quad
Q_{2}^{(3)}A=\bmat{1&2&3\\12&15&18\\7&8&9\\10&11&12},\quad
R_{14}^{(2)}A=\bmat{21&24&27\\4&5&6\\7&8&9\\10&11&12}\end{align*}
となります．この結果ともとの$A$を見比べてみると
- $P_{34}A$は第３行と第４行の入れ替え
- $Q_{2}^{(3)}A$は第２行の３倍
- $R_{14}^{(2)}A$は第１行に第４行の２倍の付け加え
という基本変形が起こっていることが分かります．
一般の基本変形もいま見た例のような正方行列$P_{ij}$, $Q_{i}^{(k)}$, $R_{ij}^{(k)}$をかけることによって引き起こすことができます．
$k\in\R$，$A$を$n$行の行列，$I$を$n$次単位行列とする．また
- $P_{ij}$を$I$の第$i$列と第$j$列を入れ替えた行列
- $Q_{i}^{(k)}$を$I$の第$(i,i)$列を$k$とした行列 ($k\neq0$)
- $R_{ij}^{(k)}$を$I$の第$i$列に第$j$列の$k\in\R$倍を加えた行列
とする．このとき，これらを行列に左からかけることで次のように行基本変形が引き起こされる：
- $P_{ij}A$は$A$の第$i$行と第$j$行を入れ替えてできる行列
- $Q_{i}^{(k)}A$は$A$の第$i$行を$k$倍してできる行列 ($k\neq0$)
- $R_{ij}^{(k)}A$は$A$の第$i$行に$A$の第$j$行の$k$倍を加えてできる行列
また，$P_{ij}$, $Q_{i}^{(k)}$, $R_{ij}^{(k)}$を$A$に右からかけると，同様の列基本変形が引き起こされる．
実際に計算することにより，この命題は容易に証明することができます．
この命題から次の系が成り立つことも分かります．
$P_{ij}$, $Q_{i}^{(k)}$, $R_{ij}^{(k)}$はいずれも正則で，それぞれ$P_{ij}$, $Q_{i}^{(1/k)}$, $R_{ij}^{(-k)}$が逆行列である．
正則性の条件
この記事の本題です．念のため正則行列の定義を確認しておきましょう．
$n$次正方行列$A$が正則 (regular)であるとは
\begin{align*}AB=BA=I_n\end{align*}
をみたす$n$次正方行列$B$が存在することをいう．このとき，$B$は$A$の逆行列 (inverse matrix)であるといい，$B$を$A^{-1}$と表す．
定義は以上の通りですが，実は$AB=I$と$BA=I$のいずれかが成り立てば$A$が正則であることが証明できます．
すなわち，以下が成り立ちます．
正方行列$A$に対して，$AB=I$または$BA=I$をみたす正方行列$B$が存在すれば，$A$は正則で$A^{-1}=B$である．
行列をかけることで基本変形が引き起こされることを用いることで証明します．証明自体は少しテクニカルなので，余裕があればフォローしてみてください．
$A$を$n$次正方行列とし，$AB=I$をみたす正方行列$B$が存在すれば$A$は正則であることを，$n$に関する数学的帰納法により示す．
[1] $n=1$のとき，$A=[a]$とすると，$AB=I$から$a\neq0$であり，$B=[a^{-1}]$である．
よって，$BA=[a^{-1}a]=[1]=I$が従う．
ただし，$A=[a]$や$B=[a^{-1}]$は１行１列の行列表示である．
[2] $n=k$のときに定理が成り立つと仮定し，$(k+1)$次正方行列$A$, $B$は$AB=I$を満たすとする．
もし$A$の第１行の成分が全て０なら積$AB$の$(1,1)$成分が０となって$AB=I$とは成り得ないから，$A$の第１行には０でない成分$a$が存在する．
よって，$A$に列基本変形を施して，$(1,1)$成分が０でない行列$A_{1}$に変形できる：
\begin{align*}A:=\bmat{*&\dots&*&a&*&\dots&*\\ *&\dots&*&*&*&\dots&*\\ \vdots&\ddots&\vdots&\vdots&\vdots&\ddots&\vdots\\ *&\dots&*&*&*&\dots&*}
\to A_1:=\bmat{a&*&\dots&*\\ *&*&\dots&*\\ \vdots&\vdots&\ddots&\vdots\\ *&*&\dots&*}.\end{align*}
さらに，$A_{1}$に行基本変形と列基本変形を施して，第１行と第１列の$(1,1)$を除く全ての成分が０であるような行列$A_{2}$に変形できる：
\begin{align*}A_1\to A_2:=\bmat{a&0&\dots&0\\ 0&*&\dots&*\\ \vdots&\vdots&\ddots&\vdots\\ 0&*&\dots&*}.\end{align*}
行基本変形と列基本変形で$A$が$A_{2}$に変形されたから，$XAY=A_{2}$となる正則行列$X$, $Y$が存在する($X$, $Y$は上で定めた$P_{ij}$, $Q_{i}^{(k)}$, $R_{ij}^{(k)}$の積となっている)．
ここで，$A_{2}$, $Y^{-1}BX^{-1}$を
\begin{align*}A_{2}=\bmat{a&\m{0}^{T}\\\m{0}&A_{3}},\quad
Y^{-1}BX^{-1}=\bmat{x&\m{y}^{T}\\\m{z}&B’}\end{align*}
とおく．$XX^{-1}=YY^{-1}=AB=I$だから，
\begin{align*}\bmat{ax&a\m{y}^{T}\\A_{3}\m{z}&A_{3}B’}
=&\bmat{a&\m{0}^{T}\\\m{0}&A_{3}}\bmat{x&\m{y}^{T}\\\m{z}&B’}
\\=&A_{2}(Y^{-1}BX^{-1})
\\=&(XAY)(Y^{-1}BX^{-1})
\\=&I_{k+1}\end{align*}
だから，
\begin{align*}ax=1,\quad
a\m{y}^{T}=\m{0}^{T},\quad
A_{3}\m{z}=\m{0},\quad
A_{3}B’=I_{k}\end{align*}
が成り立つ．よって，
- $A_{3}B’=I_{k}$と帰納法の仮定を併せて，$A_{3}$は正則で逆行列$B’$をもち，
- $a\neq0$だから$a\m{y}^{T}=\m{0}^{T}$より$\m{y}=\m{0}$が成り立ち，
- ${A_{3}}^{-1}$を$A_{3}\m{z}=\m{0}$の両辺に左からかけて$\m{z}=\m{0}$が成り立つ．
これより，$Y^{-1}BX^{-1}=\bmat{x&\m{0}^{T}\\\m{0}&B’}$となるから，
\begin{align*}AB=&(X^{-1}A_2Y^{-1})\bra{Y\bmat{x&\m{0}^{T}\\\m{0}&B’}X}
\\=&X^{-1}\bmat{a&\m{0}^{T}\\\m{0}&A_{3}}\bmat{x&\m{0}^{T}\\\m{0}&B’}X
\\=&X^{-1}\bmat{ax&\m{0}^{T}\\\m{0}&A_{3}B’}X
\\=&X^{-1}I_{k+1}X=X^{-1}X=I_{k+1},
\\BA=&\bra{Y\bmat{x&\m{0}^{T}\\\m{0}&B’}X}(X^{-1}A_2Y^{-1})
\\=&Y\bmat{x&\m{0}^{T}\\\m{0}&B’}\bmat{a&\m{0}^{T}\\\m{0}&A_{3}}Y^{-1}
\\=&Y\bmat{ax&\m{0}^{T}\\\m{0}&B’A_{3}}Y^{-1}
\\=&YI_{k+1}Y^{-1}=YY^{-1}=I_{k+1}\end{align*}
が成り立つ．よって，$A$は正則で$A^{-1}=B$である．
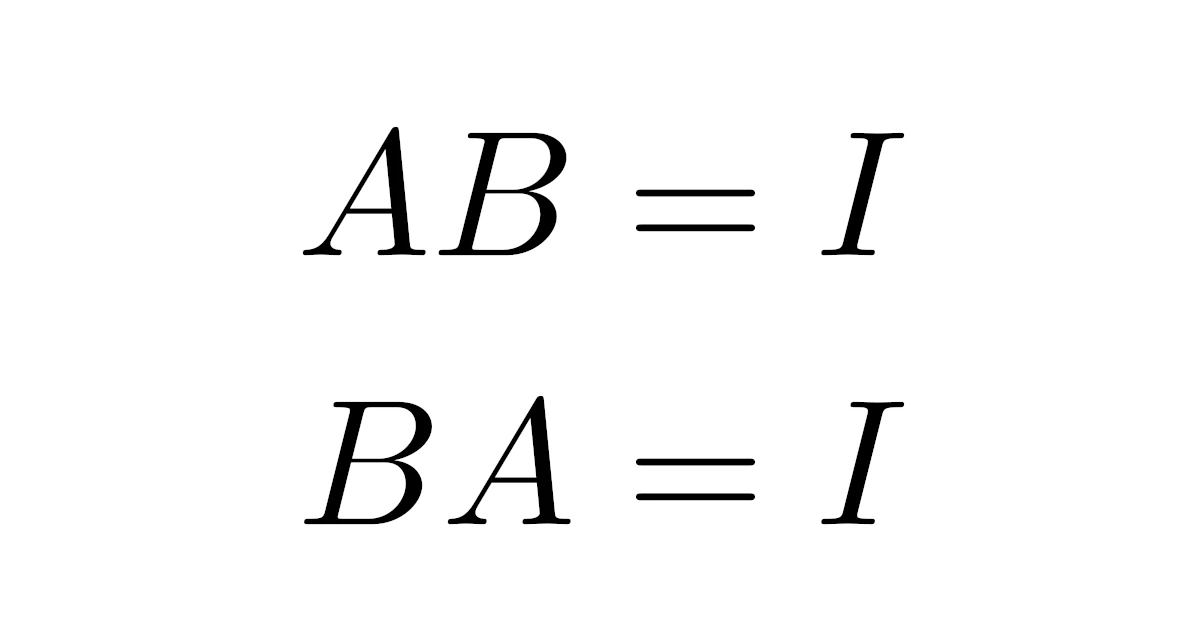
コメント