以前の記事で説明したように,例えば連立1次方程式
\begin{align*}\begin{cases}2x+3y=2\\x-y=3\\\end{cases}\end{align*}
は$A=\bmat{2&3\\1&-1}$, $\m{x}=\bmat{x\\y}$, $\m{c}=\bmat{2\\3}$とおくと$A\m{x}=\m{c}$と表すことができます.
同様に考えれば,一般に連立1次方程式は行列$A$と列ベクトル$\m{c}$を用いて$A\m{x}=\m{c}$と表すことができるのでした.
さて,連立1次方程式$A\m{x}=\m{c}$はいつでも解を持つとは限りません.また,解を持ってもひとつとは限らず,全ての解をきちんと表せることは大切です.
これらの問題については,係数行列のランク$\rank{A}$,拡大係数行列のランク$\rank{[A,\m{c}]}$を調べることで答えが得られます.
この記事では
- 係数行列・拡大係数行列・ランクの復習
- 連立1次方程式が解をもつための必要十分条件
- 連立1次方程式の解の自由度と解の一意性
を順に説明します.
なお,この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが,複素行列など一般の体を成分とする行列・ベクトルに対しても同様です.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
係数行列・拡大係数行列・ランクの復習
本題に入る前に,
- 連立1次方程式の係数行列と拡大係数行列
- 行列のランク
について復習をしておきましょう.
係数行列と拡大係数行列
連立1次方程式の係数行列と拡大係数行列は次のように定義されるのでした.
$m\times n$行列$A$と$m$次列ベクトル$\m{c}$に対し,連立1次方程式$A\m{x}=\m{c}$を考える.このとき$A$, $[A,\m{c}]$をそれぞれ係数行列 (coefficient matrix),拡大係数行列 (enlarged coefficient matrix)という.
例えば,$A=\bmat{1&2&3\\4&5&6}$, $\m{c}=\bmat{7\\8}$に対し,$\m{x}=\bmat{x\\y\\z}$の連立1次方程式$A\m{x}=\m{c}$は
\begin{align*}&\bmat{1&2&3\\4&5&6}\bmat{x\\y\\z}=\bmat{7\\8}
\\\iff&\begin{cases}x+2y+3z=7\\4x+5y+6z=8\end{cases}\end{align*}
であり,この係数行列,拡大係数行列はそれぞれ
\begin{align*}A=\bmat{1&2&3\\4&5&6},\quad
[A,\m{c}]=\bmat{1&2&3&7\\4&5&6&8}\end{align*}
ですね.
行列のランク
行列のランクを定義するためには,以下の事実が重要なのでした.
簡約行列とは
\begin{align*}&\bmat{\color{blue}{\m{1}}&0&3&0\\0&\color{blue}{\m{1}}&0&0\\0&0&0&\color{blue}{\m{1}}},\quad
\bmat{0&\color{blue}{\m{1}}&0&4\\0&0&\color{blue}{\m{1}}&2\\0&0&0&0},\quad
\bmat{\color{blue}{\m{1}}&0\\0&\color{blue}{\m{1}}\\0&0}\end{align*}
のように,
- 第$i$行から第$i+1$行に移るごとに左側から$0$が増えていき
- 各行の主成分($0$でない最も左の成分)が全て$1$であり
- 主成分のある列では主成分以外の成分が全て$0$
であるような行列のことを言うのでした.
さて,このことから行列のランクは以下のように定義されます.
行列$A$に対して,$A$に行基本変形を施して簡約行列$B$になったとき,$B$の主成分の個数を$A$のランク(階数,rank)といい,$\rank{A}$や$\operatorname{rk}{A}$などと表す.
例えば,行基本変形により
\begin{align*}\bmat{2&3&-2\\2&-2&8\\-3&0&-6}
\to&\bmat{2&3&-2\\1&-1&4\\-3&0&-6}
\to\bmat{2&3&-2\\1&-1&4\\-1&0&-2}
\\\to&\bmat{1&-1&4\\2&3&-2\\-1&0&-2}
\to\bmat{1&-1&4\\0&5&-10\\0&-1&2}
\\\to&\bmat{1&-1&4\\0&1&-2\\0&-1&2}
\to\bmat{1&-1&4\\0&1&-2\\0&0&0}\end{align*}
なので,
\begin{align*}\rank{\bmat{2&3&-2\\2&-2&8\\-3&0&-6}}=\rank{\bmat{1&-1&4\\0&1&-2\\0&0&0}}=2\end{align*}
ですね.
解をもつ連立1次方程式と解を持たない連立1次方程式
連立1次方程式が解をもつための必要十分条件を理解するために,まずは具体例を観察しておきましょう.
具体例1(解を持たない連立1次方程式)
$A=\bmat{1&1&1\\0&1&0\\0&0&0}$, $\m{c}=\bmat{1\\2\\3}$に対して,$\m{x}=\bmat{x\\y\\z}$の連立1次方程式$A\m{x}=\m{c}$は解を持つか.
素朴に掃き出し法で考えましょう.
拡大係数行列$[A,\m{c}]$を行基本変形により簡約化すると
\begin{align*}[A,\m{c}]=&\bmat{1&1&1&1\\0&1&0&2\\0&0&0&3}
\to\bmat{1&0&1&-1\\0&1&0&2\\0&0&0&3}\end{align*}
なので,もとの連立1次方程式は
\begin{align*}\begin{cases}x+z=-1\\y=2\\0=3\end{cases}\end{align*}
となる.この第3式はどのように$x,y,z$を選んでも満たしえないので,解は存在しない.
そもそも連立1次方程式の解とは未知数に代入して等式を満たす数の組のことでしたから,何を代入しても等式を満たさない場合は解は存在しないということになりますね.
具体例2(解を持つ連立1次方程式)
$A=\bmat{1&1&2\\1&2&3}$, $\m{c}=\bmat{3\\2}$に対して,$\m{x}=\bmat{x\\y\\z}$の連立1次方程式$A\m{x}=\m{c}$は解を持つか.
この問題も素朴に掃き出し法で考えましょう.
拡大係数行列$[A,\m{c}]$を行基本変形により簡約化すると
\begin{align*}[A,\m{c}]=&\bmat{1&1&2&3\\1&2&3&2}
\to\bmat{1&1&2&3\\0&1&1&-1}
\\\to&\bmat{1&0&1&4\\0&1&1&-1}\end{align*}
なので,これに対応する連立1次方程式は
\begin{align*}\begin{cases}x+z=4\\y+z=-1\end{cases}
\iff\begin{cases}x=4-z\\y=-1-z\end{cases}\end{align*}
となります.
このとき,任意の$z$に対して$x$, $y$の値が決まるから,$z=k$とおけば全ての解$(x,y,z)=(4-k,-1-k,k)$が得られる($k$は任意定数).
この問題のように解が一意に定まらない場合は,任意定数を用いることで解を表すことができます.
連立1次方程式が解をもつための必要十分条件
いまの具体例1の連立1次方程式の係数行列のランク$\rank{A}$と拡大係数行列のランク$\rank{[A,\m{c}]}$を比較すると,
\begin{align*}\rank{A}=\rank{\bmat{1&0&1\\0&1&0\\0&0&0}}=2,\quad
\rank{[A,\m{c}]}=\rank{\bmat{1&0&1&-1\\0&1&0&2\\0&0&0&3}}=3\end{align*}
となっており,このように$\rank{A}<\rank{[A,\m{c}]}$となっているとどう頑張っても成り立たない$0=a$ ($a\neq0$)の形の等式が現れて解が存在しないということが見てとれますね.
一方,具体例2では
\begin{align*}\rank{A}=\rank{\bmat{1&0&1&4\\0&1&1&1}}=2,\quad
\rank{[A,\m{c}]}=\rank{\bmat{1&0&1\\0&1&1}}=2\end{align*}
となっており,$\rank{A}=\rank{[A,\m{c}]}$となっている場合は$A$の簡約化で主成分の存在しない列に対応する未知数(いまの場合は第3列に対応する$z$)に任意定数をおくことで全ての解を表すことができます.
このことから,次の連立1次方程式が解をもつための必要十分条件が成り立つことがみてとれますね.
$m\times n$行列$A$と$m$次列ベクトル$\m{c}$に対し,次は同値である.
- $\rank{A}=\rank{[A,\m{c}]}$
- $\m{x}\in\R^n$の連立1次方程式$A\m{x}=\m{c}$は解をもつ
$[A,\m{c}]$の簡約化を$[B,\m{d}]$とする.このとき,連立1次方程式$A\m{x}=\m{c}$, $B\m{x}=\m{d}$の解は一致する.
$\rank{B}\le\rank{[B,\m{d}]}$が成り立つことに注意すると,行基本変形によるランクの不変性と併せて
\begin{align*}\rank{A}=\rank{B}\le\rank{[B,\m{d}]}=\rank{[A,\m{c}]}\end{align*}
が成り立つ.よって,$\rank{A}<\rank{[A,\m{c}]}$または$\rank{A}=\rank{[A,\m{c}]}$しかあり得ない.
[$(1)\Ra(2)$の証明] $\rank{A}=\rank{[A,\m{c}]}$のとき,$\rank{B}=\rank{[B,\m{d}]}$である.
主成分をもたない列に対応する未知数全てに任意に定数を与えることで,他の未知数も定まり解が得られる.
よって,$B\m{x}=\m{d}$は解をもつから,$A\m{x}=\m{c}$も解をもつ.
[$(2)\Ra(1)$の証明] 対偶を示す.$\rank{A}<\rank{[A,\m{c}]}$のとき,$\rank{B}<\rank{[B,\m{d}]}$である.
このとき,ある$j\in\{1,\dots,m\}$が存在して
- $B$の第$j$行の成分は全て0である
- $\m{d}$の第$j$成分は0でない
が成り立つ.このとき,連立1次方程式$B\m{x}=\m{d}$の$j$番目の方程式は$0=a$ ($a\neq0$)の形をしており$B\m{x}=\m{d}$は解をもたない.よって,$A\m{x}=\m{c}$も解をもたない.
連立1次方程式の解の自由度と解の一意性
次に連立1次方程式$A\m{x}=\m{c}$が解をもつときの解の様子をもう少し詳しく考えましょう.
定理(解の自由度)
繰り返しになりますが,先ほどの具体例2のように$\rank{A}=\rank{[A,\m{c}]}$の場合は$A$の簡約化で主成分をもたない列に対応する未知数全てに任意定数を与えることで全ての解が得られます.
このように,連立1次方程式の解を表すために必要となる解の自由度を以下のように定義します.
いま説明したように,任意定数はちょうど「主成分が存在しない列の個数分」だけ必要になりますから,以下の定理が成り立ちますね.
$m\times n$行列$A$と$m$次列ベクトル$\m{c}$に対し,$N:=\rank{A}=\rank{[A,\m{c}]}$をみたすとする.このとき,$\m{x}$の連立1次方程式$A\m{x}=\m{c}$の解の自由度は$n-N$である.
標語的には「解をもつ連立1次方程式$A\m{x}=\m{c}$の解の自由度は(未知数の個数)-$\rank{A}$」ですね.
もしくは$A$の列数と$\m{x}$の次数は等しいので,「解の自由度は($A$の次数)-$\rank{A}$」といっても同じことですね.
$[A,\m{c}]$の簡約化を$[B,\m{d}]$とする.このとき,連立1次方程式$A\m{x}=\m{c}$, $B\m{x}=\m{d}$の解は一致する.
このとき,$\rank{B}=\rank{A}=N$なので$B$の主成分が存在しない列は$(n-N)$個ある.
この$B$の主成分が存在しない列に対応する未知数全てに任意定数を与えると,$B\m{x}=\m{d}$の残りの未知数は全てそれらの任意定数で一意に表せる.
すなわち,$B\m{x}=\m{d}$の解の自由度は$n-N$なので,$A\m{x}=\m{c}$の解の自由度も$n-N$である.
すなわち,$\rank{A}(=\rank{[A,\m{c}]})$が未知数の個数に比べて小さいほど,自由度が大きいわけですね.
とくに$N=n$の場合は自由度が0となるので,次のようにいえますね.
$m\times n$行列$A$と$m$次列ベクトル$\m{c}$に対し,$n=\rank{A}=\rank{[A,\m{c}]}$が成り立てば,$\m{x}$の連立1次方程式$A\m{x}=\m{c}$の解は一意である.
斉次連立1次方程式の解の一意性
定数項が全て0の連立1次方程式は$A\m{x}=\m{0}$と表すことができますが,この連立1次方程式を斉次または同次といいます.
斉次連立1次方程式$A\m{x}=\m{0}$はどんな係数行列$A$であっても必ず零ベクトル$\m{0}$を解に持つので,この解$\m{0}$を自明解といいます.
斉次連立1次方程式$A\m{x}=\m{0}$が解を持つことだけなら,$\rank{A}=\rank{[A,\m{0}]}$と係数行列と拡大係数行列のランクが等しいことからも分かりますね.
また,斉次連立1次方程式の自明解でない解を全て非自明解といいます.
このことから,斉次連立1次方程式について
- 非自明解をもつ
- 解は一意でない
が同値であることが分かりますね.よって,上の系を踏まえると,次のように言うことができますね.
$m\times n$行列$A$が$n=\rank{A}$を満たすとき,$\m{x}$の斉次連立1次方程式$A\m{x}=\m{0}_m$は自明解のみもつ.

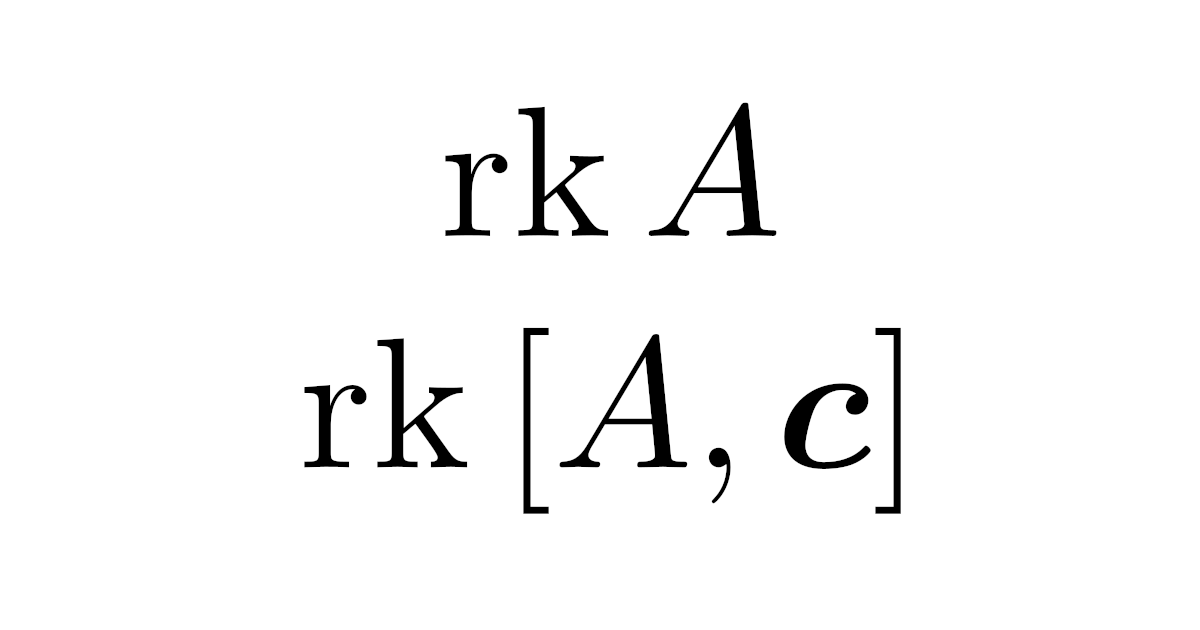


コメント