数ベクトル空間の部分空間の定義｜証明のテンプレも例題から解説

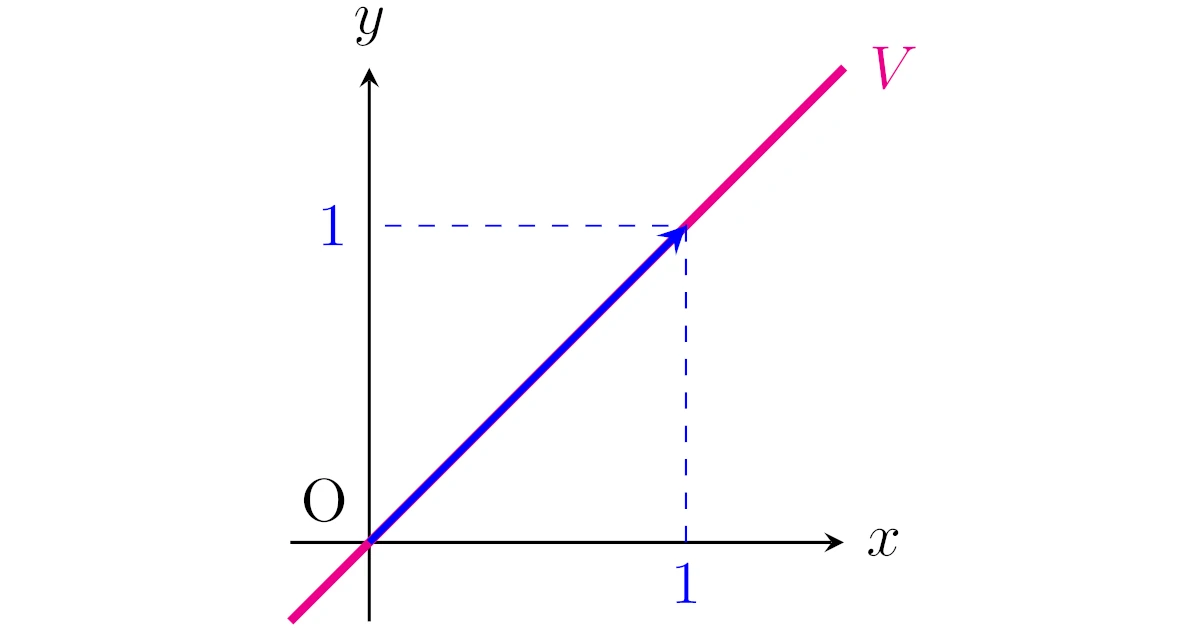
２次列ベクトル全部の集合 $R^{2}$ の部分集合

$\begin{array}{r} V = {t [\begin{array}{c} 1 \\ 1 \end{array}] | t \in R} \end{array}$

を考えましょう．この $V$ はベクトル $[\begin{matrix} 1 \\ 1 \end{matrix}]$ を実数倍してできるベクトルの集合なので，次のように図示できますね．

任意の $a, b \in V$ と $k \in R$ に対して，和 $a + b$ とスカラー倍 $k a$ が

$\begin{array}{r} a + b, k a \in V \end{array}$

を満たすことは（計算しても図形的にも）簡単に分かりますね．

このように「 $R^{n}$ の部分集合 $V$ の元のどんな和もスカラー倍も常に $V$ に属する」とき， $V$ を $R^{n}$ の部分空間といいます．

この記事では

$R^{n}$ の部分空間の定義
$R^{n}$ の部分空間の具体例
$R^{n}$ の部分空間の基本性質

を順に説明します．

なお，特に断らない限り以下では実行列・実ベクトルを扱うことにしますが，複素行列など一般の体を成分とする行列・ベクトルに対しても同様です．

「線形代数学の基本」の一連の記事

行列と列ベクトル

行列式

$R^{n}$ の部分空間と基底

正方行列の対角化

線形代数学の参考文献
1. 大学教養線形代数（加藤文元著）
2. 手を動かしてまなぶ線形代数（藤岡敦著）
部分空間の定義
部分空間の具体例
部分空間の直感的な判定

線形代数学の参考文献

以下は線形代数学に関するオススメの教科書です．

大学教養線形代数（加藤文元著）

数学科など理論系の学生向けの線形代数の入門書です．平易な例から丁寧に説明されています．

手を動かしてまなぶ線形代数（藤岡敦著）

理論と演習のバランスをとりながら勉強したい人にオススメの入門書です．

部分空間の定義

冒頭で述べた列ベクトル全部の空間 $R^{n}$ の部分空間をきちんと述べると次のようになります．

［部分空間］ $R^{n}$ の部分集合 $V$ が空でなく次の２条件を同時に満たすとき， $V$ を $R^{n}$ の部分空間（subspace）という．

任意の $a, b \in V$ に対して $a + b \in V$ が成り立つ．
任意の $k \in R$ , $a \in V$ に対して $k a \in V$ が成り立つ．

要は $V$ の任意の元を和とスカラー倍で計算しても $V$ の外に出ることがないということなので，この２つの条件をそれぞれ

$V$ は和について閉じている
$V$ はスカラー倍について閉じている

といいます．

実はより一般に線形空間というものが定義され，線形空間の部分集合で線形空間の性質を満たす集合を線形部分空間と呼びます．

しかし， $R^{n}$ 上の部分空間について考えれば本質的な部分は十分に理解できるので，この線形代数の基本の一連の記事では $R^{n}$ 上の部分空間のみについて説明します．

部分空間の具体例

それでは，いくつか部分空間を紹介していきます．

例１（自明な部分空間１）

まずは簡単な部分空間をひとつ考えましょう．

$R^{2}$ の部分集合 $V$ として $R^{2}$ 自身を考える．すなわち， $V = R^{2}$ とする．

このとき， $V$ が $R^{2}$ の部分空間となることを示せ．

定義通りに $V$ が和とスカラー倍について閉じていることを示しましょう．

任意の $a, b \in V (= R^{2})$ と $k \in R$ に対して， $a + b, k a$ はもちろん $V$ の元である．すなわち，

$\begin{array}{r} a + b, k a \in V \end{array}$

なので， $V$ は $R^{2}$ の部分空間である．

一般に $R^{n}$ に対して $R^{n}$ 自身はいつでも $R^{n}$ の部分空間となります．

このように $R^{n}$ はいつでも $R^{n}$ の部分空間になることから， $R^{n}$ は $R^{n}$ の自明な部分空間（trivial subspace）と呼ばれます．

例２（自明な部分空間２）

もうひとつ簡単な部分空間を考えましょう．

$R^{2}$ の部分集合 $V$ として零ベクトル $0$ のみからなる集合を考える．すなわち， $V = {0}$ とする．

このとき， $V$ が $R^{2}$ の部分空間となることを示せ．

やはり定義通りに $V$ が和とスカラー倍について閉じていることを示しましょう．

任意の $a, b \in V (= {0})$ と $k \in R$ をとる．

このとき， $V$ は $0$ のみからなる集合なので，もちろん $a = b = 0$ である．よって，

$\begin{array}{r} a + b = 0, k a = 0 \end{array}$

となって $a + b, k a \in V$ と分かるから， $V$ は $R^{2}$ の部分空間である．

一般に $R^{n}$ に対して零ベクトルのみからなる集合 ${0}$ はいつでも $R^{n}$ の部分空間となります．

このように， $R^{n}$ の ${0}$ もいつでも部分空間になることから， ${0}$ も $R^{n}$ と同じく自明な部分空間（trivial subspace）と呼ばれます．

例３（ $R^{2}$ の部分空間）

次に冒頭で挙げた集合 $V$ が部分空間であることを示しましょう．

$R^{2}$ の部分集合

$\begin{array}{r} V = {t [\begin{array}{c} 1 \\ 1 \end{array}] | t \in R} \end{array}$

が $R^{2}$ の部分空間となることを示せ．

$V$ は $[\begin{matrix} 1 \\ 1 \end{matrix}]$ の実数倍のベクトル（第１成分と第２成分が等しいベクトル）を全て集めてきた集合というわけですね．

$V$ が $R^{2}$ の部分集合で， $[\begin{matrix} 0 \\ 0 \end{matrix}] \in V$ だから $V$ は空でない．

［１］和について閉じていることを示す．任意に $a, b \in V$ をとる．

このとき， $V$ の定義から $a = t [\begin{matrix} 1 \\ 1 \end{matrix}]$ , $b = t^{'} [\begin{matrix} 1 \\ 1 \end{matrix}]$ ( $t, t^{'} \in R$ )と表せるから，

$\begin{array}{r} a + b = t [\begin{array}{c} 1 \\ 1 \end{array}] + t^{'} [\begin{array}{c} 1 \\ 1 \end{array}] = (t + t^{'}) [\begin{array}{c} 1 \\ 1 \end{array}] \end{array}$

となる．これは $[\begin{matrix} 1 \\ 1 \end{matrix}]$ の実数倍のベクトルなので $a + b \in V$ である．

すなわち， $a + b \in V$ が成り立つ．

［２］スカラー倍について閉じていることを示す．任意に $a \in V$ , $k \in R$ ( $t \in R$ )をとる．

このとき， $V$ の定義から $a = t [\begin{matrix} 1 \\ 1 \end{matrix}]$ ( $t \in R$ )と表せるから，

$\begin{array}{r} k a = k (t [\begin{array}{c} 1 \\ 1 \end{array}]) = (k t) [\begin{array}{c} 1 \\ 1 \end{array}] \end{array}$

となる．これは $[\begin{matrix} 1 \\ 1 \end{matrix}]$ の実数倍のベクトルなので $k a \in V$ である．

［１］と［２］より $V$ は和とスカラー倍に閉じているから $R^{2}$ の部分空間である．

例４（ $R^{3}$ の部分空間１）

次のような集合も例３と同様に部分空間になることが分かります．

$R^{3}$ の部分集合

$\begin{array}{r} V = {[\begin{array}{c} x \\ y \\ z \end{array}] \in R^{3} | 2 x + y - z = 0} \end{array}$

が $R^{3}$ の部分空間となることを示せ．

$V$ は2×(第１成分)+(第２成分)-(第３成分)=0を満たす $R^{3}$ 上のベクトルを全て集めてきた集合で，図示すると $x y z$ 空間上の平面 $2 x + y - z = 0$ となりますね．

$V$ が $R^{3}$ の部分集合で， $[\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}] \in V$ だから $V$ は空でない．

［１］和について閉じていることを示す．任意に $a = [\begin{matrix} x \\ y \\ z \end{matrix}], b = [\begin{matrix} x^{'} \\ y^{'} \\ z^{'} \end{matrix}] \in V$ をとる．

このとき， $V$ の定義から $2 x + y - z = 0$ と $2 x^{'} + y^{'} - z^{'} = 0$ を満たす．ここで，

$\begin{array}{r} a + b = [\begin{array}{c} x \\ y \\ z \end{array}] + [\begin{array}{c} x^{'} \\ y^{'} \\ z^{'} \end{array}] = [\begin{array}{c} x + x^{'} \\ y + y^{'} \\ z + z^{'} \end{array}] \end{array}$

であり，この2×(第１成分)+(第２成分)-(第３成分)$は

$\begin{aligned} 2 (x + x^{'}) + (y + y^{'}) - (z + z^{'}) \\ = & (2 x + y - z) + (2 x^{'} + y^{'} - z^{'}) = 0 \end{aligned}$

となっている．よって， $a + b \in V$ が成り立つ．

［２］スカラー倍について閉じていることを示す．任意に $a = [\begin{matrix} x \\ y \\ z \end{matrix}] \in V$ , $k \in R$ をとる．

このとき， $V$ の定義から $2 x + y - z = 0$ を満たす．ここで，

$\begin{array}{r} k a = k [\begin{array}{c} x \\ y \\ z \end{array}] = [\begin{array}{c} k x \\ k y \\ k z \end{array}] \end{array}$

であり，この2×(第１成分)+(第２成分)-(第３成分)は

$\begin{aligned} 2 (k x) + (k y) - (k z) = & k (2 x + y - z) \\ = & k \times 0 = 0 \end{aligned}$

となっている．これより $k a \in V$ が成り立つ．

［１］と［２］より $V$ は和とスカラー倍に閉じているから $R^{3}$ の部分空間である．

例５（ $R^{3}$ の部分空間２）

条件を２つ以上もつ次の $V$ も $R^{3}$ 部分空間です．

$R^{3}$ の部分集合

$\begin{array}{r} V = {[\begin{array}{c} x \\ y \\ z \end{array}] \in R^{3} | \begin{array}{c} x + y + z = 0, \\ x - y + z = 0 \end{array}} \end{array}$

が $R^{3}$ の部分空間となることを示せ．

$V$ は

(第１成分)+(第２成分)+(第３成分)=0
(第１成分)-(第２成分)+(第３成分)=0

の両方を満たす $R^{3}$ 上のベクトルを全て集めてきた集合で，図示すると $x y z$ 空間上の平面 $x + y + z = 0$ と平面 $x - y + z = 0$ の交線となりますね．

条件の数が増えても部分空間であることを示すためにやることは同じです．

$V$ が $R^{3}$ の部分集合で， $[\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}] \in V$ だから $V$ は空でない．

［１］和について閉じていることを示す．任意に $a = [\begin{matrix} x \\ y \\ z \end{matrix}], b = [\begin{matrix} x^{'} \\ y^{'} \\ z^{'} \end{matrix}] \in V$ をとる．

このとき， $V$ の定義から $x + y + z = 0$ , $x - y + z = 0$ と $x^{'} + y^{'} + z^{'} = 0$ , $x^{'} - y^{'} + z^{'} = 0$ を満たす．ここで，

であり，

(第１成分)+(第２成分)+(第３成分)は
$\begin{aligned} (x + x^{'}) + (y + y^{'}) + (z + z^{'}) \\ = & (x + y + z) + (x^{'} + y^{'} + z^{'}) = 0 \end{aligned}$
(第１成分)-(第２成分)+(第３成分)は
$\begin{aligned} (x + x^{'}) - (y + y^{'}) + (z + z^{'}) \\ = & (x - y + z) + (x^{'} - y^{'} + z^{'}) = 0 \end{aligned}$

となっている．よって， $a + b \in V$ が成り立つ．

［２］スカラー倍について閉じていることを示す．任意に $a = [\begin{matrix} x \\ y \\ z \end{matrix}] \in V$ , $k \in R$ をとる．

このとき， $V$ の定義から $x + y + z = 0$ , $x - y + z = 0$ を満たす．ここで，

$\begin{array}{r} k a = k [\begin{array}{c} x \\ y \\ z \end{array}] = [\begin{array}{c} k x \\ k y \\ k z \end{array}] \end{array}$

であり，

(第１成分)+(第２成分)+(第３成分)は
$\begin{array}{r} (k x) + (k y) + (k z) = k (x + y + z) = 0 \end{array}$
(第１成分)-(第２成分)+(第３成分)は
$\begin{array}{r} (k x) - (k y) + (k z) = k (x - y + z) = 0 \end{array}$

となっている．これより $k a \in V$ が成り立つ．

［１］と［２］より $V$ は和とスカラー倍に閉じているから $R^{3}$ の部分空間である．

例６（ $R^{3}$ の部分空間３）

次の空間も本質的には例５までと何も変わりません．

$A = [\begin{matrix} 2 & 3 & - 1 \\ 3 & 1 & 1 \end{matrix}]$ とする． $R^{3}$ の部分集合

$\begin{array}{r} V = {x \in R^{3} | A x = 0} \end{array}$

が $R^{3}$ の部分空間となることを示せ．

$V$ は左から行列 $A$ をかけて $0$ となるベクトルを全て集めてきた集合ですね．

あくまで和とスカラー倍について閉じていることを示すだけですね．

$V$ が $R^{3}$ の部分集合で空でないことは明らか．

［１］和について閉じていることを示す．任意に $a, b \in V$ をとる．

このとき， $V$ の定義から $A a = 0$ , $A b = 0$ を満たすから，

$\begin{array}{r} A (a + b) = A a + A b = 0 \end{array}$

となっている．よって， $a + b \in V$ が成り立つ．

［２］スカラー倍について閉じていることを示す．任意に $a \in V$ , $k \in R$ をとる．

このとき， $V$ の定義から $A a = 0$ を満たすから，

$\begin{array}{r} A (k a) = k (A a) = k 0 = 0 \end{array}$

となっている．これより $k a \in V$ が成り立つ．

［１］と［２］より $V$ は和とスカラー倍に閉じているから $R^{3}$ の部分空間である．

$x = [\begin{matrix} x \\ y \\ z \end{matrix}]$ として $A x = 0$ を成分で表すと

$\begin{array}{r} {\begin{cases} 2 x + 3 y - z = 0 \\ 3 x + y + z = 0 \end{cases} \end{array}$

なので，例５と同じようにして成分で示すこともできます．

しかし，行列は積について分配法則を満たしますから，いまの解答例のように行列のまま考える方が楽ですね．

なお，例５の $V$ を $V = {[\begin{matrix} x \\ y \\ z \end{matrix}] \in R^{3} | [\begin{matrix} 1 & 1 & 1 \\ 1 & - 1 & 1 \end{matrix}] [\begin{matrix} x \\ y \\ z \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}]}$ と書き換えると，例６のように示すこともできますね．

例６のように左から行列 $A$ をかけて零ベクトル $0$ となるベクトル $x$ 全部の集合を行列 $A$ の核といいます．

部分空間の直感的な判定

次に部分空間が満たす基本性質を紹介します．

部分空間の基本性質

$V$ を $R^{n}$ の部分空間とする．このとき，次が成り立つ．

$0 \in V$
任意の $a, b \in V$ , $k, ℓ \in R$ に対して $k a + ℓ b \in V$

言葉で説明すれば，それぞれ

$V$ は必ず零ベクトル $0$ を持つ
$V$ に属する２つのベクトルをどのように伸ばして足し合わせても $V$ の元である

と言うことができますね．

(1) $V$ は部分空間だからスカラー倍について閉じており，任意の $a \in V$ に対して $0 = 0 a \in V$ が成り立つ．

(2) $V$ は部分空間だからスカラー倍について閉じており $k a, ℓ b \in V$ が成り立つ．

さらに，和についても閉じているから $k a + ℓ b \in V$ が成り立つ．

このことから， $R^{n}$ の部分空間は直感的には，原点を通り「真っ直ぐ」に伸びた空間ということができますね．

部分空間であるための必要十分条件

実はいまの命題の(2)は $V$ が部分空間であるための必要十分条件となっています．

$R^{n}$ の空でない部分集合 $V$ に対して，次は同値である．

$V$ は部分空間である．
任意の $a, b \in V$ , $k, ℓ \in R$ に対して $k a + ℓ b \in V$ が成り立つ．

$(1) ⟹ (2)$ は上の命題で証明した．

また，(2)が成り立つとき， $k = ℓ = 1$ とすれば $a + b \in V$ が成り立ち， $ℓ = 0$ とすれば $k a \in V$ が成り立つから， $V$ は和とスカラー倍について閉じているから $(2) ⟹ (1)$ も成り立つ．

この定理があるため，教科書によってはこの(2)の性質をみたす集合 $V$ を $R^{n}$ の部分空間と定義していることもあります．

部分空間でない例

今の次に部分空間でない例を考えます．

$R^{2}$ の部分集合

$\begin{aligned} V = {[\begin{array}{c} t \\ 1 + t \end{array}] | t \in R}, \\ W = {[\begin{array}{c} t \\ t^{2} \end{array}] | t \in R} \end{aligned}$

はともに $R^{2}$ の部分空間とはならないことを示せ．

上の基本性質で説明したように $V$ は零ベクトル $0$ が属していない時点で部分空間でないと分かります．

また，部分空間は和とスカラー倍で閉じているため「真っ直ぐ」な空間となっているはずで， $W$ のように曲がっていると部分空間でないと分かります．

このことを踏まえてきちんと書くと次のようになります．

$0 \notin V$ だから， $V$ は部分空間ではない．

$[\begin{matrix} 1 \\ 1 \end{matrix}], [\begin{matrix} - 1 \\ 1 \end{matrix}] \in W$ であるが

$\begin{array}{r} [\begin{array}{c} 1 \\ 1 \end{array}] + [\begin{array}{c} - 1 \\ 1 \end{array}] = [\begin{array}{c} 0 \\ 2 \end{array}] \notin W \end{array}$