ℝⁿの部分空間の基底と次元を求める方法を具体例から解説

例えば，$\R^3$の基底として

$\begin{align*}\anb{\bmat{1\\0\\0},\bmat{0\\1\\0},\bmat{0\\0\\1}},\quad\anb{\bmat{1\\1\\1},\bmat{-2\\-2\\1},\bmat{0\\1\\-1}}\end{align*}$

が挙げられます．

$\R^3$の他の基底も考えてみると分かってくるのですが，実は$\R^3$の基底はいつでも３個のベクトルからなります．

このことはより一般に成り立ち，任意の$\R^n$の部分空間において基底をなすベクトルの個数は一定であることが証明できます．

そこで，$\R^n$の部分空間$V$の基底をなすベクトルの個数を$V$の次元といいます．

この記事では

$\R^n$の部分空間の次元の定義
$\R^n$の部分空間の次元の具体例
基底をなすベクトルの個数が一定であることの証明

を順に説明します．

なお，特に断らない限り以下では実行列・実ベクトルを扱うことにしますが，複素行列など一般の体を成分とする行列・ベクトルに対しても同様です．

この記事の内容は一般の線形空間でも同様に成り立ちますが，簡単のためここでは$\R^n$の部分空間に限って話を進めます．

「線形代数学の基本」の一連の記事

行列と列ベクトル

行列式

$\R^n$の部分空間と基底

固有値と固有ベクトル

線形代数学の参考文献
1. 大学教養線形代数（加藤文元著）
2. 手を動かしてまなぶ線形代数（藤岡敦著）
$\R^n$の部分空間の次元の定義
$\R^n$の部分空間の次元の具体例
基底をなすベクトルの個数が一定であることの証明

線形代数学の参考文献

以下は線形代数学に関するオススメの教科書です．

大学教養線形代数（加藤文元著）

数学科など理論系の学生向けの線形代数の入門書です．平易な例から丁寧に説明されています．

手を動かしてまなぶ線形代数（藤岡敦著）

理論と演習のバランスをとりながら勉強したい人にオススメの入門書です．

$\R^n$の部分空間の次元の定義

冒頭でも説明したように次の定理が成り立ちます（この記事の最後に証明しています）．

$\R^n$の部分空間$V$が２つの基底$\anb{\m{a}_1,\m{a}_2,\dots,\m{a}_k}$, $\anb{\m{b}_1,\m{b}_2,\dots,\m{b}_\ell}$をもつとき$k=\ell$が成り立つ．

この定理を踏まえて，次のように次元を定義します．

$\R^n$の部分空間$V$の基底がなすベクトルの個数を$V$の次元（dimension）といい$\dim{V}$と表す．

また，自明な部分空間$\{\m{0}\}$の次元は$0$と定める．

$\anb{\m{a}_1,\m{a}_2,\dots,\m{a}_n}$が基底なら$\m{a}_1,\m{a}_2,\dots,\m{a}_n$は線形独立なので，直感的には$\m{a}_1,\m{a}_2,\dots,\m{a}_n$たちの線形結合で$n$方向に広がった空間を表せるわけですね．

このことから次元は空間が広がっている「方向」の数を表すといえるわけですね．

具体的には$\R^2$が縦横の２方向，$\R^3$が縦横高さの３方向で空間を表現できることからも直感的に受け入れやすいですね．

高校数学でも，平面ベクトルの問題は２つのベクトルを基準，空間ベクトルの問題は３つのベクトルを基準にして考えることが多かったのは，$\R^2$のどの基底も２つのベクトルからなり，$\R^3$のどの基底も３つのベクトルからなることが背景にあるわけですね．

$\R^n$の部分空間の次元の具体例

いくつかの$\R^n$の部分空間について，具体的に次元を求めましょう．

例１（$\R^2$の次元）

$\dim{\R^2}$を求めよ．

前回の記事で証明したように，

$\begin{align*}\anb{\bmat{1\\0},\bmat{0\\1}}\end{align*}$

は$\R^2$の基底である．

この基底は２個のベクトルからなるので$\dim{\R^2}=2$である．

一般に$\R^n$は$n$個のベクトルからなる基底

$\begin{align*}\anb{\bmat{1\\0\\\vdots\\0},\bmat{0\\1\\\vdots\\0},\dots,\bmat{0\\0\\\vdots\\1}}\end{align*}$

をもつので，$\dim{\R^n}=n$となりますね．

この基底を$\R^n$の標準基底というのでした．

例２（$\R^2$の１次元部分空間）

$\R^2$の部分空間$V$を

$\begin{align*}V=\set{\bmat{x\\y}\in\R^2}{x-2y=0}\end{align*}$

で定めるとき，$\dim{V}$を求めよ．

$\bmat{x\\y}\in V$は$y=\dfrac{1}{2}x$を満たすので，$V$を図示すると$xy$平面上の直線$y=\dfrac{1}{2}x$となりますね．

言い換えると，第１成分が第２成分の$2$倍であるようなベクトルの空間ですから，$V$上の全ての元が$\bmat{2\\1}$の実数倍で表されます．

よって，基底は$\anb{\bmat{2\\1}}$となって$\dim{V}=1$となりそうです．

$x-2y=0$なら$\bmat{x\\y}=\bmat{2y\\y}$だから，

$\begin{align*}V=&\set{\bmat{2y\\y}}{y\in\R} \\=&\set{y\bmat{2\\1}}{y\in\R} =\spn{\bra{\bmat{2\\1}}}\end{align*}$

となり，$V$の全ての元は$\bmat{2\\1}$の線形結合で表せる．

また，一般に１つのみのベクトルは線形独立だから$\bmat{2\\1}$は線形独立である．

したがって，$\anb{\bmat{2\\1}}$は$V$の基底であり，この基底は１個のベクトルからなるので$\dim{V}=1$である．

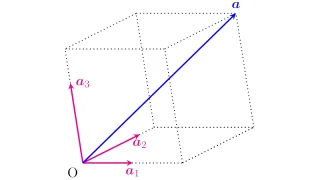
例３（$\R^3$の２次元部分空間）

$\R^3$の部分空間$V$を

$\begin{align*}V=\set{\bmat{x\\y\\z}\in\R^3}{x-2y-3z=0}\end{align*}$

で定めるとき，$\dim{V}$を求めよ．

$V$を図示すると$xyz$平面上の平面$x-2y-3z=0$となりますね．

$\dim{\R^2}=2$だったように，平面の部分空間は２つのベクトルからなる基底をもち次元は$2$となりそうです．

$x-2y-3z=0$なら$\bmat{x\\y\\z}=\bmat{2y+3z\\y\\z}$だから，

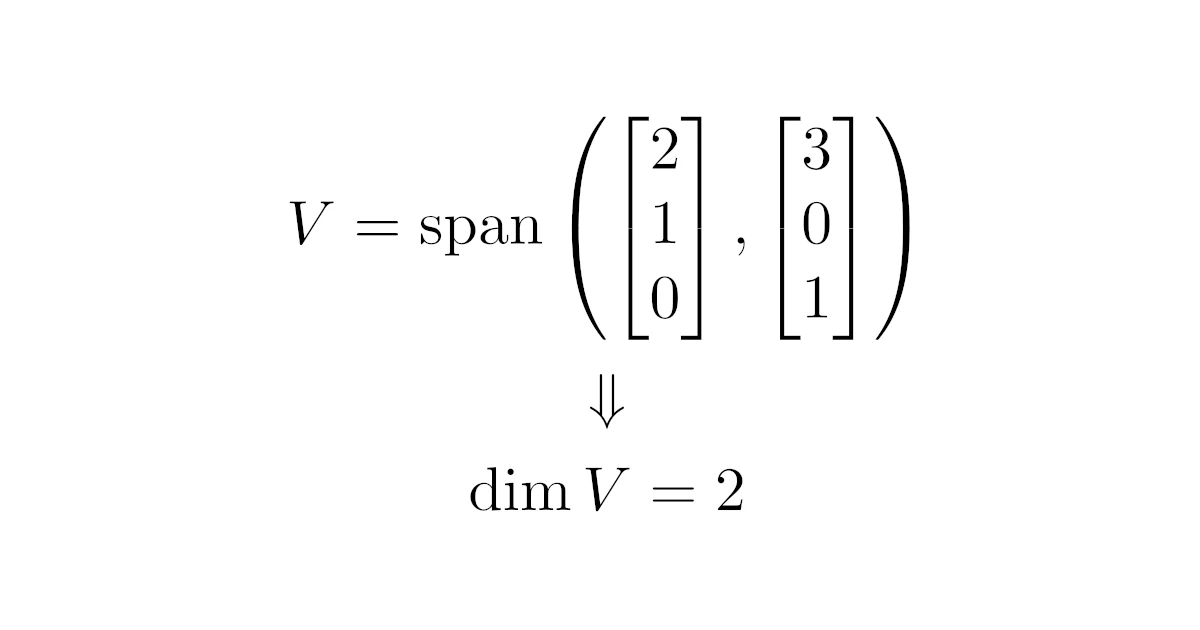
$\begin{align*}V=&\set{\bmat{2y+3z\\y\\z}}{y,z\in\R} \\=&\set{y\bmat{2\\1\\0}+z\bmat{3\\0\\1}}{y,z\in\R} =\spn{\bra{\bmat{2\\1\\0},\bmat{3\\0\\1}}}\end{align*}$

と書き換えられるから，$V$の全ての元は$\bmat{2\\1\\0},\bmat{3\\0\\1}$の線形結合で表せる．

また，この２つのベクトルを並べてできる行列のランクは

$\begin{align*}\rank{\bmat{2&3\\1&0\\0&1}}=\rank{\bmat{1&0\\0&1\\0&0}}=2\end{align*}$

だから$\bmat{2\\1\\0},\bmat{3\\0\\1}$は線形独立である．

したがって，$\anb{\bmat{2\\1\\0},\bmat{3\\0\\1}}$は$V$の基底であり，この基底は２個のベクトルからなるので$\dim{V}=2$である．

一般に$\m{a}_1,\m{a}_2,\dots,\m{a}_r\in\R^n$が$\rank{[\m{a}_1,\m{a}_2,\dots,\m{a}_r]}=r$を満たせば$\m{a}_1,\m{a}_2,\dots,\m{a}_r$は線形独立なのでした．

これについて詳しくは以下の記事を参照してください．

線形独立性の考え方を例題から解説｜ランクとの関係も解説

行列のランクは基本変形によって求めるのが基本ですが，ベクトルの「線形独立性」をもとにしても同じ物を考えることができます．この記事では，列ベクトルの線形独立性を例題から説明し，ランクとの関係を説明します．

例４（$\R^4$の２次元部分空間）

$\R^4$の部分空間$V$を

$\begin{align*}V=\set{\bmat{x\\y\\z\\w}\in\R^4}{\begin{gathered}x+y+3z+w=0\\x-y-z+2w=0\end{gathered}}\end{align*}$

で定めるとき，$\dim{V}$を求めよ．

例３までが理解できていれば，集合の条件式からベクトルの文字の個数を減らして，どのベクトルで生成されているかを考えれば良さそうですね．

連立１次方程式$\begin{cases}x+y+3z+4w=0\\x-y-z+2w=0\end{cases}$を$x,y$について解くと，

$\begin{align*}x=-z-3w,\quad y=-2z-w\end{align*}$

となるので，このとき$\bmat{x\\y\\z\\w}=\bmat{-z-3w\\-2z-w\\z\\w}$だから，

$\begin{align*}V=&\set{\bmat{-z-3w\\-2z-w\\z\\w}}{z,w\in\R} \\=&\set{z\bmat{-1\\-2\\1\\0}+w\bmat{-3\\-1\\0\\1}}{y,z\in\R} =\spn{\bra{\bmat{-1\\-2\\1\\0},\bmat{-3\\-1\\0\\1}}}\end{align*}$

と書き換えられるから，$V$の全ての元は$\bmat{-1\\-2\\1\\0},\bmat{-3\\-1\\0\\1}$の線形結合で表せる．

また，この２つのベクトルを並べてできる行列のランクは

$\begin{align*}\rank{\bmat{-1&-3\\-2&-1\\1&0\\0&1}}=\rank{\bmat{1&0\\0&1\\0&0\\0&0}}=2\end{align*}$

だから$\bmat{-1\\-2\\1\\0},\bmat{-3\\-1\\0\\1}$は線形独立である．

したがって，$\bmat{-1\\-2\\1\\0},\bmat{-3\\-1\\0\\1}$は$V$の基底であり，この基底は２個のベクトルからなるので$\dim{V}=2$である．

例３でもし条件式がなければ$\R^3$で，例４でもし条件式がなければ$\R^4$です．

しかし，実際には

例３は条件式が１つあることで次元が$1$落ちて$\dim{V}=\dim{\R^3}-1=2$
例４は条件式が２つあることで次元が$2$落ちて$\dim{V}=\dim{\R^4}-2={}2$

となっているわけですね．

つまり，直感的には空間が広がっている「方向」の数が次元でしたから，（本質的に新しい）条件が１つ加わるごとに空間の「方向」がひとつ減って次元が落ちるわけですね．

基底をなすベクトルの個数が一定であることの証明

それでは最後に冒頭で紹介した次元の定義のもととなった次の定理を証明しましょう．

（再掲）$\R^n$の部分空間$V$が２つの基底$\anb{\m{a}_1,\m{a}_2,\dots,\m{a}_k}$, $\anb{\m{b}_1,\m{b}_2,\dots,\m{b}_\ell}$が得られたとき$k=\ell$が成り立つ．

背理法により示す．$k<\ell$と仮定する．

$\anb{\m{a}_{1},\dots,\m{a}_{k}}$は$V$の基底なので，$\m{b}_{1},\dots,\m{b}_{k}$は$\m{a}_{1},\dots,\m{a}_{k}$の線形結合で表せる．

$\begin{align*}\m{b}_{i}=p_{i1}\m{a}_{1}+\dots+p_{ik}\m{a}_{k}\quad(i=1,\dots,k).\end{align*}$

このとき，

$\begin{align*}[\m{b}_{1},\dots,\m{b}_{k}]=[\m{a}_{1},\dots,\m{a}_{k}]P\quad \bra{P:=\bmat{p_{11}&\dots&p_{1k}\\\vdots&\ddots&\vdots\\p_{1k}&\dots&p_{kk}}}\end{align*}$

である．いま$\m{a}_{1},\dots,\m{a}_{k}$は線形独立だから$[\m{a}_{1},\dots,\m{a}_{k}]$は正則行列で，同様に$[\m{b}_{1},\dots,\m{b}_{k}]$も正則行列だから$P$は正則である．

よって，

$\begin{align*}[\m{b}_{1},\dots,\m{b}_{k}]P^{-1}=[\m{a}_{1},\dots,\m{a}_{k}]\end{align*}$

となって，$\m{a}_{1},\dots,\m{a}_{k}$はいずれも$\m{b}_{1},\dots,\m{b}_{k}$の線形結合で表せる．

また，$\m{b}_{k+1}$は$\m{a}_{1},\dots,\m{a}_{k}$の線形結合で表せるから，$\m{b}_{k+1}$は$\m{b}_{1},\dots,\m{b}_{k}$の線形結合で表せることになり，$\m{b}_{1},\dots,\m{b}_{k},\m{b}_{k+1}$が線形独立であることに矛盾する．

$k>\ell$と仮定した場合も同様に矛盾が導かれるから，結局$k=\ell$が得られる．