${}0$以外の実数は全て逆数を持ちますが，零行列$O$でない正方行列$A$であっても逆行列を持たないことはよくあります．
そこで，正方行列$A$が逆行列$A^{-1}$を持つかどうかの判定する方法の１つに，行列$A$のランクを利用する方法があります．
また，正則性の判定条件の副産物として，正方行列$A$の逆行列$A^{-1}$を求めることができるようになります．
そこで，この記事では
- 行列のランク（階数）を定義するための準備
- 行列のランク（階数）
- 正方行列の正則性の判定と逆行列の求め方
を順に説明します．
なお，この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが，複素行列など一般の体を成分とする行列・ベクトルに対しても同様です．
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
線形代数学の参考文献
以下は線形代数学に関するオススメの教科書です．
大学教養 線形代数（加藤文元 著）
数学科など理論系の学生向けの線形代数の入門書です．平易な例から丁寧に説明されています．
手を動かしてまなぶ 線形代数（藤岡敦 著）
理論と演習のバランスをとりながら勉強したい人にオススメの入門書です．
行列のランク（階数）を定義するための準備
まずは行列のランクを定義するために必要な簡約行列を目指して説明します．
階段行列の定義
まずは階段行列を定義します．１つ下の行に移るにつれて左から０が増えていく
\begin{align*}
\bmat{\color{blue}\m{*}&\color{blue}\dots&\color{blue}*&\color{blue}*&\color{blue}\dots&\color{blue}*&\color{blue}*&\color{blue}\dots&\color{blue}*&\color{blue}*
\\0&\dots&0&\color{blue}\m{*}&\color{blue}\dots&\color{blue}*&\color{blue}*&\color{blue}\dots&\color{blue}*&\color{blue}*
\\0&\dots&0&0&\dots&0&\color{blue}\m{*}&\color{blue}\dots&\color{blue}*&\color{blue}*
\\\vdots&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots}
\end{align*}
のような形の行列を階段行列といいます．例えば，
\begin{align*}
&\bmat{\color{blue}\m{1}&\color{blue}2&\color{blue}3&\color{blue}4\\0&\color{blue}\m{1}&\color{blue}0&\color{blue}-2\\0&0&0&\color{blue}\m{1}},\quad
\bmat{0&\color{blue}\m{1}&\color{blue}5&\color{blue}8\\0&0&\color{blue}\m{-3}&\color{blue}2\\0&0&0&0},\quad
\bmat{\color{blue}\m{4}&\color{blue}0\\0&\color{blue}\m{3}\\0&0}
\end{align*}
はいずれも階段行列です．
また，階段行列の各行の０でない一番左の成分（上の式で太字になっている成分）をその行の主成分といいます．ただし，全ての成分が０の行には主成分が存在しないとします．
きちんと階段行列の定義を述べると以下のようになりますが，上の例でどういうものか分かっていればきちんと読めなくても問題ありません．
$m\times n$行列$A=(a_{ij})$が階段形（echelon form）または階段行列（echelon matrix）あるとは，任意の$i\in\{1,\dots,m-1\}$に対して，次が成り立つことをいう．
- $m\ge2$なら$a_{2,1}=0$
- $a_{i,k}=0$ ($k=1,\dots,j$, $j<n$)なら，$a_{i+1,k}=0$ ($k=1,\dots,j+1$)である．
- $a_{i,k}=0$ ($k=1,\dots,n$)なら，$a_{i+1,k}=0$ ($k=1,\dots,n$)である．
また，階段行列において，零ベクトルでない行の０でない最も左の成分を，その行の主成分（pivot, pivot element）という．
簡約行列の定義
階段行列の主成分が全て１であり，主成分が存在する列の主成分以外の成分が全て０である
\begin{align*}\bmat{\color{blue}\m{1}&\color{blue}\dots&\color{blue}*&\color{blue}0&\color{blue}\dots&\color{blue}*&\color{blue}0&\color{blue}\dots&\color{blue}*&\color{blue}*
\\0&\dots&0&\color{blue}\m{1}&\color{blue}\dots&\color{blue}*&\color{blue}0&\color{blue}\dots&\color{blue}*&\color{blue}*
\\0&\dots&0&0&\dots&0&\color{blue}\m{1}&\color{blue}\dots&\color{blue}*&\color{blue}*
\\\vdots&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots}\end{align*}
のような行列を簡約行列といいます．例えば，
\begin{align*}\bmat{\color{blue}\m{1}&\color{blue}0&\color{blue}3&\color{blue}0\\0&\color{blue}\m{1}&\color{blue}0&\color{blue}0\\0&0&0&\color{blue}\m{1}},\quad
\bmat{0&\color{blue}\m{1}&\color{blue}0&\color{blue}4\\0&0&\color{blue}\m{1}&\color{blue}2\\0&0&0&0},\quad
\bmat{\color{blue}\m{1}&\color{blue}0\\0&\color{blue}\m{1}\\0&0}\end{align*}
はいずれも簡約行列です．
次を満たす階段行列を簡約行列（reduced matrix）という．
- 主成分は全て１である．
- 主成分の存在する列において，主成分以外の成分はすべて０である．
行列の簡約化
さて，掃き出し法と同様に考えれば，簡約行列に関して次の命題が成り立ちます．
任意の行列は行基本変形により簡約行列に変形できる．
例えば，行列$\bmat{2&3&-2\\2&-2&8\\-3&0&-6}$は行基本変形により
\begin{align*}\bmat{2&3&-2\\2&-2&8\\-3&0&-6}
\to&\bmat{2&3&-2\\1&-1&4\\-3&0&-6}
\to\bmat{2&3&-2\\1&-1&4\\-1&0&-2}
\\\to&\bmat{1&-1&4\\2&3&-2\\-1&0&-2}
\to\bmat{1&-1&4\\0&5&-10\\0&-1&2}
\\\to&\bmat{1&-1&4\\0&1&-2\\0&-1&2}
\to\bmat{1&0&2\\0&1&-2\\0&0&0}\end{align*}
と簡約行列に変形できますね．
行列$A$を行基本変形により簡約行列$B$に変形することを簡約化（reduction）という．また，簡約行列$B$自体も$A$の簡約化という．
上の例より$\bmat{2&3&-2\\2&-2&8\\-3&0&-6}$の簡約化は$\bmat{1&0&2\\0&1&-2\\0&0&0}$ですね．
行列のランク（階数）
どんな行列も簡約化できることは上の命題で説明した通りですが，実は簡約化の主成分の個数は一意に定まることが証明できます．
このことがランクの定義に重要な役割を果たします．
簡約化の主成分の個数の一意性
［簡約化の主成分の個数の一意性］行列の簡約化の主成分の個数は，簡約化の仕方によらず一定である．
簡約化も一意に定まりますが，ここではそこまで証明しません．
証明は少々テクニカルなので，余裕のあればフォローするくらいでひとまずは問題ないでしょう．
背理法により示す．すなわち，行列$m\times n$行列$A$を行基本変形を施して，
- 主成分を$r$個もつ簡約行列$B=[\m{b}_{1},\dots,\m{b}_{n}]$
- 主成分を$s$個もつ簡約行列$C=[\m{c}_{1},\dots,\m{c}_{n}]$
のどちらにもなり得るとして矛盾を導く（$s<r$）．
このとき，任意の$k\in\{1,\dots,n\}$に対して，$\m{b}_{k}$の第$r+1$成分以下は全て0であり，$\m{c}_{k}$の第$s+1$成分以下は全て０であることに注意する．
さらに，$B$の主成分以外の成分がすべて0になるように列基本変形を施してできる行列を$B_{1}$とする．
また，同様に$C$の主成分が存在する列$\m{e}_{\ell}$（$\ell=1,\dots,s$）が第$\ell$列になるように列基本変形を施し，主成分以外の成分がすべて0になるように列基本変形を施してできる行列を$C_{1}$とする．
このとき，
\begin{align*}B_{1}=\bmat{I_{r}&O\\O&O},\quad
C_{1}=\bmat{I_{s}&O\\O&O}\end{align*}
である．
行基本変形$A\to B$, $A\to C$を引き起こす行列をそれぞれ$S$, $T$とし，列基本変形$B\to B_{1}$, $C\to C_{1}$を引き起こす行列をそれぞれ$S’$, $T’$とすると，$SA=B$, $TA=C$, $BS’=B_{1}$, $CT’=C_{1}$が成り立つ．
$S$, $T$, $S’$, $T’$はいずれも正則行列なので，$A=S^{-1}B$, $A=T^{-1}C$, $B=B_{1}S’^{-1}$, $C=C_{1}T’^{-1}$だから，
\begin{align*}&S^{-1}B_{1}S’^{-1}=T^{-1}C_{1}T’^{-1}
\\\iff&TS^{-1}B_{1}S’^{-1}T’=C_{1}\end{align*}
を得る．
このとき，$TS^{-1}$, $S’^{-1}T’$, $B_{1}$, $C_{1}$を
\begin{align*}TS^{-1}=\bmat{U_{1}&U_{2}\\U_{3}&U_{4}},\quad
S’^{-1}T’=\bmat{U’_{1}&U’_{2}\\U’_{3}&U’_{4}},\quad
U_{1},U’_{1}\in\Mat_{r}(\R)\end{align*}
となるように適当な行列$U_{k}$, $U’_{k}$（$k=1,\dots,4$）で表すと，
\begin{align*}C_{1}=&TS^{-1}B_{1}S’^{-1}T’
\\=&\bmat{U_{1}&O\\U_{3}&O}\bmat{U’_{1}&U’_{2}\\U’_{3}&U’_{4}}
\\=&\bmat{U_{1}U’_{1}&U_{1}U’_{2}\\U_{3}U’_{1}&U_{3}U’_{2}}\end{align*}
となる．よって，
\begin{align*}I_{r}=U_{1}U’_{1},\quad
O=U_{1}U’_{2},\quad
O=U_{3}U’_{1}\end{align*}
が成り立つ．一般に$r$次正方行列$X,Y$が$I_r=XY$を満たせば$X,Y$は共に正則だから，$I_{r}=U_{1}U’_{1}$より$U’_{1}$は正則となる．
そこで，${U’_{1}}^{-1}$を$O=U_{3}U’_{1}$の両辺に右からかけて$U_{3}=O$を得る．よって，
- $C_{1}$の第$r+1$行以降の成分はすべて０となるが，
- $C_{1}$の$(r+1,r+1)$成分は１
だから矛盾する．
行列のランク（階数）の定義
いま証明した定理［簡約化の主成分の個数の一意性］から，どんな行列も簡約化したときの主成分の個数は一定となりますね．
このことから，次のようにランクを定義することができます．
行列$A$に行基本変形を施して簡約行列$B$になったとき，$B$の主成分の個数を$A$のランク（階数，rank）といい，
\begin{align*}\operatorname{rank}{A},\quad\operatorname{rk}{A}\end{align*}
などと表す．
定義が矛盾なく機能することを「定義がwell-definedである」といいます．今の場合は「定理［簡約化の主成分の個数の一意性］からランクはwell-definedである」と表現することができます．
例えば，上でみたように$\bmat{2&3&-2\\2&-2&8\\-3&0&-6}$の簡約化は$\bmat{1&0&2\\0&1&-2\\0&0&0}$で，この簡約行列の主成分の個数は２なので，
\begin{align*}\rank{\bmat{2&3&-2\\2&-2&8\\-3&0&-6}}=\rank{\bmat{1&0&2\\0&1&-2\\0&0&0}}=2\end{align*}
となるわけですね．
行基本変形でたどり着いた簡約行列の主成分の個数がランクなので，行列$A,B$が行基本変形で移り合う場合は$\rank{A}=\rank{B}$となることは当たり前にしておきましょう．
行列の正則性の判定と逆行列の求め方
それでは，ランクと行列の正則性の関係を説明します．
正則性の必要十分条件
ランクから正方行列が正則行列（逆行列を持つ）かどうかの必要十分条件を与えることができます．
［正則性の必要十分条件］$n$次正方行列$A$について，次は同値である．
- $\rank{A}=n$を満たす．
- $A$は正則行列である．
［$(1)\Ra(2)$の証明］$\rank{A}=n$なら，ランクの定義から$A$の簡約化の主成分が$n$個存在する．$A$が$n$次正方行列であることと併せて$A$の簡約化は$I$である．
よって，行基本変形でこの簡約化を引き起こす正則行列$P$が存在して$PA=I$となるから，$A$は正則である．
［$(2)\Ra(1)$の証明］$A$の簡約化を$B$とすると，この行基本変形を引き起こす正則行列$P$が存在して$PA=B$が成り立ち，$\rank{A}=\rank{B}$が成り立つ．
一般に正則行列の積は正則行列なので，$B$のどの行も零ベクトルではないから，$B$の主成分は$n$個存在することになり$\rank{B}=n$が従う．
よって，$\rank{A}=n$を得る．
一般に行列のランクのような「１つの対象に固有なもの」を不変量（invariant）といいます．
ランクという不変量から正方行列の正則性の必要十分条件が分かるように，数学において不変量が重要な役割を果たすことはよくあります．
逆行列の求め方
いま示した定理より，$n$次正方行列$A$が正則行列なら$\rank{A}=n$なので$A$の簡約化は単位行列$I$ということになります．
このことを用いると，具体的に逆行列を求める際に非常に実用的な以下の系が成り立ちます．
$n$次正方行列$A$を正則行列とする．行列$[A,I]$の簡約化が$[I,B]$であれば，$A$は正則で$B=A^{-1}$である．
行基本変形$[A,I]\to[I,B]$を引き起こす正則行列を$P$とすると，$[PA,PI]=[I,B]$が成り立つから$PA=I$かつ$P=B$である．
よって，$BA=I$が成り立つ．
一般に$n$次正方行列$X,Y$が$I_n=XY$を満たせば$X,Y$は共に正則だから，$A$は正則で$B=A^{-1}$である．
逆行列を求める具体例
いま示した系を用いて具体的に逆行列を求めてみましょう．
$A:=\bmat{1&2&1\\0&2&3\\1&2&2}$の逆行列を求めよ．
行基本変形により
\begin{align*}[A,I]=&\bmat{1&2&1&1&0&0\\0&2&3&0&1&0\\1&2&2&0&0&1}
\to\bmat{1&2&1&1&0&0\\0&2&3&0&1&0\\0&0&1&-1&0&1}
\\\to&\bmat{1&2&0&2&0&-1\\0&2&0&3&1&-3\\0&0&1&-1&0&1}
\to\bmat{1&0&0&-1&-1&2\\0&2&0&3&1&-3\\0&0&1&-1&0&1}
\\\to&\bmat{1&0&0&-1&-1&2\\0&1&0&3/2&1/2&-3/2\\0&0&1&-1&0&1}\end{align*}
となるから
\begin{align*}A^{-1}=\bmat{-1&-1&2\\3/2&1/2&-3/2\\-1&0&1}=\frac{1}{2}\bmat{-2&-2&4\\3&1&-3\\-2&0&2}\end{align*}
である．
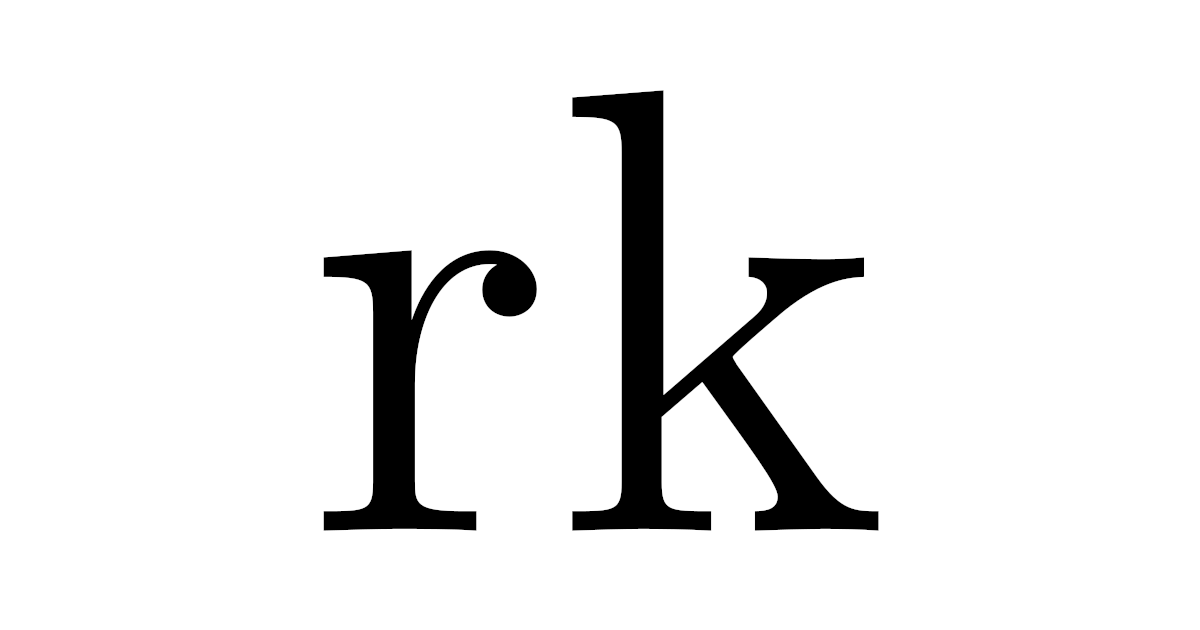
コメント