行列式の図形的イメージ｜正則性が判定できる行列式の考え方

正方行列$A$に対して，$AB=BA=I$となる正方行列$B$が存在するとき，$A$を正則行列というのでした．

正方行列の正則性は線形代数学の様々な概念と繋がっているため，正方行列が正則であるかどうかを判定できることは大切です．

その判定法する方法は様々あり，行列式というものを用いることでも正方行列の正則性を判定することができます．

この記事では

２次正方行列の行列式
３次以上の正方行列の行列式

を順に説明します．

なお，この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが，複素行列など一般の体を成分とする行列・ベクトルに対しても同様です．

「線形代数学の基本」の一連の記事

行列と列ベクトル

行列式

$\R^n$の部分空間と基底

正方行列の対角化

線形代数学の参考文献
1. 大学教養線形代数（加藤文元著）
2. 手を動かしてまなぶ線形代数（藤岡敦著）
２次正方行列の行列式
３次以上の正方行列の行列式

線形代数学の参考文献

以下は線形代数学に関するオススメの教科書です．

大学教養線形代数（加藤文元著）

数学科など理論系の学生向けの線形代数の入門書です．平易な例から丁寧に説明されています．

手を動かしてまなぶ線形代数（藤岡敦著）

理論と演習のバランスをとりながら勉強したい人にオススメの入門書です．

２次正方行列の行列式

最初に２次正方行列の行列式について説明します．

平行と線形独立

２次正方行列の考え方を理解するためには，線形独立性についての次の命題がベースになります．

零ベクトルでない２次列ベクトル$\m{a},\m{b}$に対して，次は同値である．

$\m{a}$と$\m{b}$は平行である
$\m{a}$と$\m{b}$は線形従属である

この命題は３次以上の列ベクトルでも成り立ちますが，ここでは２次正方行列を考えるため２次列ベクトルで述べています．

［$(1)\Ra(2)$の証明］$\m{a}$と$\m{b}$が平行なら，$\m{a}=t\m{b}$なる$t\in\R$が存在する．$\m{a}$は零ベクトルでないから$t\neq0$である．

$\m{a}=t\m{b}$の右辺を移項して，$t\neq0$に注意すると$\m{a}-t\m{b}=\m{0}$は$\m{a}$, $\m{b}$の非自明な線形関係である．

すなわち，$\m{a}$と$\m{b}$は線形従属である．

［$(2)\Ra(1)$の証明］$\m{a}$と$\m{b}$が線形従属なら，非自明な線形関係$k\m{a}+\ell\m{b}=\m{0}$が存在する．

また，このとき$k=0$なら$\m{b}\neq\m{0}$と併せて$\ell=0$となるから$k\m{a}+\ell\m{b}=\m{0}$が非自明な線形関係であることに矛盾する．よって，$k\neq0$である．

よって，$k\m{a}+\ell\m{b}=\m{0}$の両辺を$k$で割って整理すると$\m{a}=-\frac{\ell}{k}\m{b}$となるから$\m{a}$と$\m{b}$は平行である．

この命題の対偶を考えると，次の系が従いますね．

零ベクトルでない２次列ベクトル$\m{a},\m{b}$に対して，次は同値である．

$\m{a}$と$\m{b}$は平行でない
$\m{a}$と$\m{b}$は線形独立である

列ベクトル$\m{a},\m{b}$が線形独立性であるとは「全てのベクトルが完全にバラバラな向きを向いていること」というイメージでしたから，このイメージとも一致しますね．

また，次の命題も当たり前にしておきましょう．

２次列ベクトル$\m{a},\m{b}$が線形独立なら，$\m{a},\m{b}$はどちらも零ベクトルでない．

もし$\m{a}=\m{0}$なら，非自明な線形関係

$\begin{align*}1\m{a}+0\m{b}=\m{0}\end{align*}$

が成り立つから，$\m{a},\m{b}$が線形独立であることに矛盾する．

同様に$\m{a}=\m{0}$のときも矛盾するから，$\m{a},\m{b}$はどちらも零ベクトルでない．

２次列ベクトルがつくる平行四辺形の面積

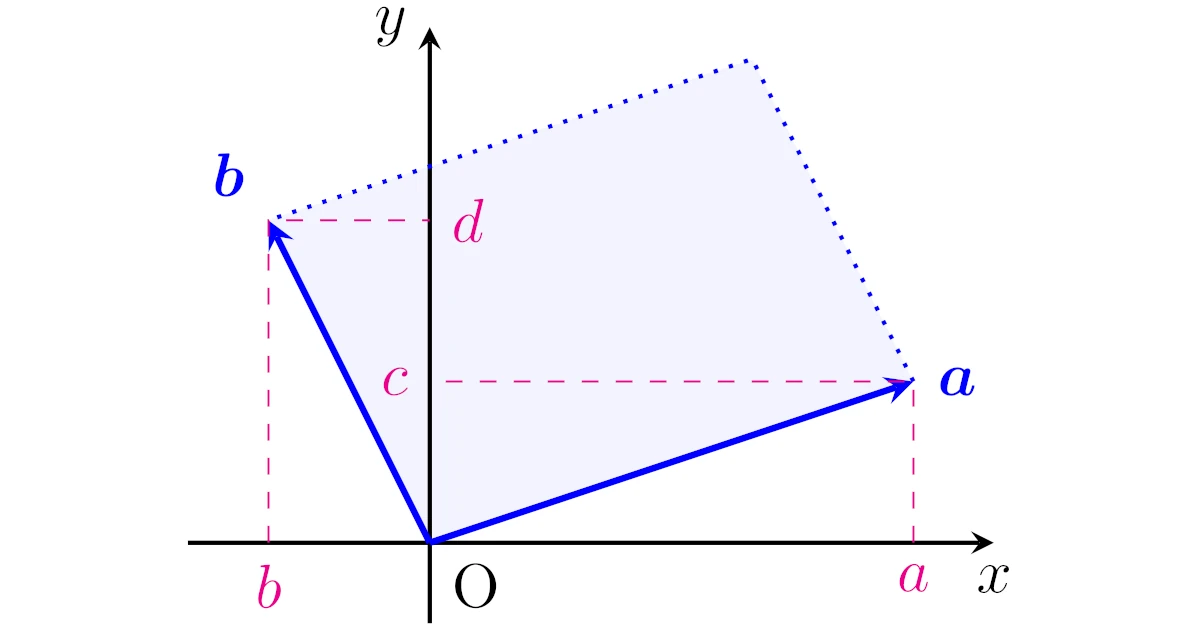
２次列ベクトル$\m{a}=\bmat{a\\c}$, $\m{b}=\bmat{b\\d}$を考え，この２つのベクトルがつくる以下の平行四辺形を考えましょう．

「$\m{a}=\m{0}$または$\m{b}=\m{0}$」もしくは「$\m{a}\m{b}\neq\m{0}$で$\m{a},\m{b}$が平行」のときは，面積が０の「潰れた」平行四辺形とみなします．

このとき，さきほど確認したことから$\m{a}$, $\m{b}$が線形独立であることと，この平行四辺形の面積が０でないことは同値になりますね．

さて，高校数学で学ぶようにこの平行四辺形の面積は$|ad-bc|$でしたから，まとめると次が成り立つと言えますね．

２次列ベクトル$\m{a}=\bmat{a\\c}$, $\m{b}=\bmat{b\\d}$に対して，以下は同値である．

$\m{a}$, $\m{b}$は線形独立である．
$ad-bc\neq0$が成り立つ．

さて，２次列ベクトル$\m{a}$, $\m{b}$は線形独立であることと，２次正方行列$[\m{a},\m{b}]$が正則行列であることは同値でしたから，さらに次が成り立ちますね．

２次正方行列$A=\bmat{a&b\\c&d}$に対して，以下は同値である．

$A$は正則行列である．
$ad-bc\neq0$が成り立つ．

２次正方行列の行列式の定義と具体例

このことを踏まえて，以下のように２次正方行列の行列式を定義します．

２次正方行列$A=\bmat{a&b\\c&d}$に対し，$ad-bc$を$A$の行列式（determinant）といい，$|A|$や$\det{A}$などと表す．

つまり，$|A|=ad-bc$が０であるか否かを調べるだけで，$A=\bmat{a&b\\c&d}$の正則性が判定できるというわけですね．

いくつか具体例を考えましょう．

２次正方行列$A,B,C$を

$\begin{align*}A:=\bmat{1&2\\3&4},\quad B:=\bmat{1&1\\2&2},\quad C:=\bmat{0&-2\\3&\pi}\end{align*}$

と定める．このとき，それぞれ行列式を求め，正則性を判定せよ．

行列式の定義より

$\begin{align*}&|A|=1\cdot4-2\cdot3=-2, \\&|B|=1\cdot2-1\cdot2=0, \\&|C|=0\cdot\pi-(-2)\cdot3=6\end{align*}$

である．行列式が０であることと，その行列が正則であることは同値なので，$A$, $C$は正則であり$B$は正則でない．

３次以上の正方行列の行列式

２次正方行列の場合と同様に，３次正方行列$A=[\m{a},\m{b},\m{c}]$に対しては，$\m{a},\m{b},\m{c}$が張る平行六面体の体積に相当するものを$|A|$と定めれば

$\m{a}$, $\m{b}$, $\m{c}$が線形独立でない
$|A|=0$

が同値であることがみてとれますね．

つまり，$\m{a}$, $\m{b}$, $\m{c}$が同一平面上にあれば平行六面体は「潰れて」体積が０となりますし，この逆も成り立ちます．

一般に，$n$次正方行列$A=[\m{a}_{1},\dots,\m{a}_{n}]$に対しては，$\m{a}_{1},\dots,\m{a}_{n}$がつくる「平行立体の$n$次元体積」に相当するものを$|A|$と定めれば，

$\m{a}_{1},\dots,\m{a}_{n}$が線形独立でない
$|A|=0$

は同値となります．

しかし，この考え方では４次元以上の「体積」を考えることになるのでイメージするのは難しいですね．

そこで，$n$次正方行列のイメージは「平行立体の$n$次元体積」なのですが，実際に定義する際には置換を用いることが多いです．

そこで，一般の正方行列の行列式を定義するため，次の記事では置換について解説します．