行列の積はどうしてこうなる？｜行列とベクトルの考え方

線形代数学は理系大学生の多くが大学初年度に学ぶことになります．

線形代数では行列とベクトルが線形代数の最初に定義され，行列のイメージが掴めないまま抽象的な議論に進んでしまい，ずるずると線形代数を苦手としてしまうパターンはかなり多いように思います．

しかし，線形代数とは「中学校以来扱ってきた比例$y=ax$の変数$x$を複数の変数(多変数)にするとどうなるのか」ということを考える分野で，そのことが理解できると色々なところが見通しよく考えられるようになります．

そのため，この記事では最初に行列とベクトルのイメージを掴むところから説明します．

また，行列の積をどうしてそのように定義するのか理解に苦しむ人も多いのですが，これも「多変数の比例」のイメージが掴めていると自然な発想に基づいていることが分かります．

なお，この記事では実数$\R$を中心に説明しますが，複素数$\C$など一般の体に対しても同様です．

「線形代数学の基本」の一連の記事はこちら

・行列と数ベクトル
【線形代数１｜行列の計算の基本！行列の積はなぜこうなる？】←今の記事
【線形代数２｜連立１次方程式の掃き出し法と行列の基本変形】
【線形代数３｜正則の条件を簡単に！基本変形と行列の積の話】
【線形代数４｜行列のランクと，行列が逆行列をもつための条件】
【線形代数５｜連立１次方程式が解をもつ条件と解の自由度】
【線形代数６｜線形独立のイメージと線形独立であるための条件】

・行列式
【線形代数７｜行列の正則性を判定できる行列式のイメージ】
【線形代数８｜行列式を定義するための置換の性質を理解する】
【線形代数９｜「行列式」は線形代数の要！定義と性質を解説】
【線形代数10｜[余因子展開]と[行列式による正則条件]を解説】

・部分空間と基底
【線形代数11｜数ベクトル空間の部分空間と基底の考え方】
【線形代数12｜部分空間の同型と部分空間の次元(準備中)】
【線形代数13｜線形写像の像と核と次元定理(準備中)】
【線形代数14｜部分空間の和空間と共通部分の空間(準備中)】

・固有値と固有ベクトル
【線形代数15｜「固有値」「固有ベクトル」「対角化」とは？】
【線形代数16｜固有値と固有ベクトルは２ステップで求める！】
【線形代数17｜固有値・固有ベクトルの基本性質のまとめ】
【線形代数18｜固有空間はなぜ大切か？対角化の必要十分条件】

1 行列とベクトル
2 行列とベクトルの計算
3 逆行列
4 掃き出し法
5 参考文献
- 5.1 線型代数入門

行列とベクトル

ここでは，行列とベクトルの定義をイメージから説明します．

多変数の「比例」

実数$a$に対して$y=ax$が成り立つとき，「$y$は$x$に比例する」といい，$a$を比例係数というのでした．

様々にある関数の中でも$f(x)=ax$で定まる比例の関数$f$は非常に分かりやすい関数のため，他の関数よりも比較的容易に理解することができますね．

ここで，比例を「拡張」することを考えます．

例えば，２つの等式

$\begin{align*} \begin{cases} y_1=x_1+2x_2+3x_3\\ y_2=4x_1+5x_2+6x_3 \end{cases} \end{align*}$

を考えましょう．

比例$y=ax$では$x$と$y$が１つずつでしたが，この２つの等式では

$x$が$x_1$, $x_2$, $x_3$の３つ
$y$が$y_1$と$y_2$の２つ

に増えているわけですね．

つまり，比例では$x$に値を代入すれば$y$の値が分かったように，上の式では$x_1$, $x_2$, $x_3$に値を代入すれば$y_1$, $y_2$の値が分かるという状況になっています．

線形代数では，これを

$\begin{align*} \bmat{y_1\\y_2}=\bmat{1&2&3\\4&5&6}\bmat{x_1\\x_2\\x_3} \end{align*}$

のように表します．つまり，右辺では係数部分と変数部分を分けているわけですね．

このとき，

左辺を$\m{y}:=\bmat{y_1\\y_2}$
右辺の係数部分を$A:=\bmat{1&2&3\\4&5&6}$
右辺の変数部分を$\m{x}:=\bmat{x_1\\x_2\\x_3}$

とおくと，上の等式は$\m{y}=A\m{x}$と表すことができ，あたかも$A$を「比例定数」とし$\m{y}$は$\m{x}$に「比例」していると捉えることができます．

これについて，

$\m{x}$, $\m{y}$のように一列に成分を並べたものを数ベクトル
$A$のように長方形型に成分を並べたものを行列

といいます．

行列の定義

いまみた行列をきちんと定義しておきましょう．

集合$S$の元を

横に$n$個
縦に$m$個

並べたものを$S$成分の$m\times n$行列 (matrix)という：

$\begin{align*} \bmat{a_{11}&\dots&a_{1n}\\\vdots&\ddots&\vdots\\a_{m1}&\dots&a_{mn}}\quad \bra{\begin{gathered} a_{ij}\in S;\\ i=1,\dots,m,\\ j=1,\dots,n \end{gathered}}. \end{align*}$

また，この行列を$(a_{ij})_{1 \le i \le m,1 \le j \le n}$や単に$(a_{ij})$などと表し，$S$成分の$m\times n$行列全部の集合を$\Mat_{mn}(S)$などと表す．

とくに，$n\times n$行列を$n$次正方行列 (square matrix)または単に$n$次行列といい，$S$成分の$n$次西方行列全部の集合を$\Mat_{n}(S)$などと表す．

一連の記事では$S=\R$または$S=\C$の場合がほとんどで

$\Mat_{mn}(\R)$の元を実行列 (real matrix)
$\Mat_{mn}(\C)$の元を複素行列 (complex matrix)

といいます．例えば，

$A:=\bmat{1&2&3\\4&5&6}$は$2\times3$実行列で
$B:=\bmat{1&2+i&3-i\\2-i&5&0\\3+i&0&9}$は$3$次複素正方行列

ですね．

また，行列の一部を次のようによびます．

行列$(a_{ij})$に対して

$a_{pq}$を第$(p,q)$成分
$\bmat{a_{q1}&\dots&a_{qn}}$を第$p$行
$\bmat{a_{1p}\\\vdots\\a_{np}}$を第$q$列

という．

例えば，$A:=\bmat{1&2&3\\4&5&6}$は$2\times3$行列に対して

$A$の第$(1,2)$成分は$2$
$A$の第$2$行は$\bmat{4&5&6}$
$A$の第$3$列は$\bmat{3\\6}$は

ですね．

ベクトルの定義

次にベクトルを以下のように定義します．

集合$S$に対して，$S$成分の

$n\times1$行列を$n$次列ベクトル (column vector)
$1\times n$行列を$n$次行ベクトル (row vector)

という．また，$S$成分の$n$次列ベクトルを$S^{n}$と表す．

行列とベクトルの定義から分かるように，$S^{n}:=\Mat_{n1}(S)$ですね．

行列と同様に

$\R^{n}$の元を実ベクトル (real vector)
$\C^{n}$の元を複素ベクトル (complex vector)

といいます．

例１

列ベクトルについて

$\bmat{1\\2\\3}\in\N^{3}$
$\bmat{\sqrt{3}\\\sqrt{3}\\\sqrt{3}}\in\R^{3}$
$\bmat{1\\i\\0\\-i}\in\C^{4}$

です．

また，行ベクトルはコンマ“,”を用いて，$[a_{11},\dots,a_{1n}]$のようにも表します．たとえば，

$[1,2,3]\in\Mat_{13}(\N)$
$[\sqrt{3},\sqrt{3},\sqrt{3}]\in\Mat_{13}(\R)$
$[1,i,0,-i]\in\Mat_{14}(\C)$

ですね．

例２

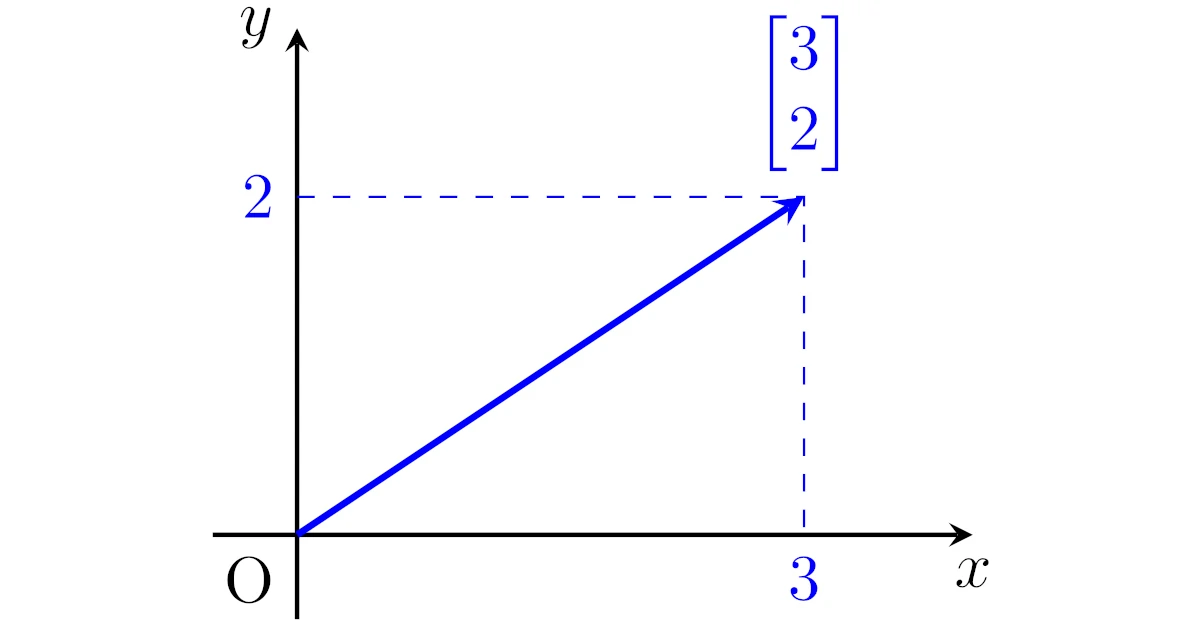
$\R^n$は$n$本の座標軸のある直交座標として考えることができます．

例えば，$\m{a}:=\bmat{3\\1}\in\R^2$は

と$xy$平面上に表せます．

例３

行列を並べることによって，行列を表すこともあります．

例えば，行列$A:=\bmat{1&2&3\\4&5&6\\7&8&9}$は

行列$A_1:=\bmat{1&2\\4&5}$, $A_2:=\bmat{3\\6}$, $A_3:=[7,8]$, $A_4:=[9]$によって，
$\begin{align*} A=\bmat{A_{1}&A_{2}\\A_{3}&A_{4}} \end{align*}$
行ベクトル$\m{b}_1=[1,2,3]$, $\m{b}_2=[4,5,6]$, $\m{b}_3=[7,8,9]$によって，
$\begin{align*} A=\bmat{\m{b}_{1}\\\m{b}_{2}\\\m{b}_{3}} \end{align*}$

などと表すことができます．

基本的な行列とベクトル

成分が全て$0$のベクトル，行列をそれぞれ零ベクトル (zero vector)，零行列 (zero matrix)という．

$A\in\Mat_{n}(\R)$について，第$(k,k)$成分 ($k=1,\dots,n$)を$A$の対角成分 (diagonal element)といい，対角成分以外の成分が$0$なら$A$を対角行列 (diagonal matrix)という．第$(k,k)$成分が$a_{k}$の対角行列を$\diag{(a_{1},\dots,a_{n})}$などと表す．

とくに，対角成分が全て１の対角行列$\diag{(1,\dots,1)}$を単位行列 (identity matrix)という．

零ベクトルは$\m{0}$，零行列は$O$，単位行列は$I$と表すことが多く，次数を明示するときには，添え字として

$\m{0}_{n}$：$n$次零ベクトル
$O_{mn}$：$m\times n$次零行列
$O_{n}$：$n$次零行列
$I_{n}$：$n$次単位行列

とするのが普通です．

単位行列はドイツ語でEinheitsmatrixと表記することから，$E$で表すこともよくあります．

例えば

$\diag{(1,2)}=\bmat{1&0\\0&2}$
$\diag{(\sqrt{2},-\sqrt{2},\sqrt{2})}=\bmat{\sqrt{2}&0&0\\0&-\sqrt{2}&0\\0&0&\sqrt{2}}$
$\diag{(1,-1,0)}=\bmat{1&0&0\\0&-1&0\\0&0&0}$

はいずれも対角行列であり，

$I_2=\bmat{1&0\\0&1}$
$I_3=\bmat{1&0&0\\0&1&0\\0&0&1}$

はいずれも単位行列ですね．

行列$A$の第$(i,j)$成分を第$(j,i)$成分にとり直した行列を$A$の転置行列 (transposed matrix)といい，${}^{t}A$, $A^{T}$などと表す．

すなわち，$A=(a_{ij})$とすると，$A^{T}={}^{t}A=(a_{ji})$である．

たとえば，$A=\bmat{1&2\\3&4\\5&6}$, $B=\bmat{2\\-3\\1}$に対して

${}^{t}A=A^{T}=\bmat{1&3&5\\2&4&6}$
${}^{t}B=B^{T}=[2,-3,1]$

ですね．

転置行列について，以下は明らかでしょう．

任意の行列$A$に対して，$A$の転置行列の転置行列は$A$である．すなわち，$(A^{T})^{T}=A$である．

行列とベクトルの計算

単なる$\alpha\in\R$を行列やベクトルと区別してスカラー (scalar)といいます．

scalar(スカラー)はラテン語で「梯子」を意味するscalaが語源となっています．また，「目盛り」や「縮尺」を意味する英語のscale(スケール)もラテン語のscalaが語源となっています．

このことから，行列やベクトルとは違い，スカラーは「量」を表すというニュアンスが感じられますね．

行列のスカラー倍と和，差

$A=(a_{ij}), B=(b_{ij})\in\Mat_{mn}(\R)$とする．このとき，$A=(a_{ij})$の$\alpha\in\R$倍と，和/差$A\pm B$をそれぞれ

$\alpha A
=\bmat{\alpha a_{11}&\dots&\alpha a_{1n}\\\vdots&\ddots&\vdots\\\alpha a_{m1}&\dots&\alpha a_{mn}}$
$A\pm B
=\bmat{a_{11}\pm b_{11}&\dots&a_{1n}\pm b_{1n}\\\vdots&\ddots&\vdots\\a_{m1}\pm b_{m1}&\dots&a_{mn}\pm b_{mn}}$　(複号同順)

で定義する．

すなわち，$\alpha$倍は全ての成分に$\alpha$をかければ良く，和と差は同じ成分同士で和と差を取れば良いわけですね．

ベクトルは行列の特別な場合(行または列が１つの行列)なので，ベクトルについても同様に$\alpha\in\R$倍と和が定義されます．

$\m{a}\in\R^n$に対して，$\m{a}+\m{a}’=\m{0}$となる$\m{a}’\in\R^n$を$\m{a}$の逆ベクトル (inverse vector)といい，$\m{a}’=-\m{a}$と表す．

$\m{a}\in\R^n$の逆ベクトル$-\m{a}$は$(-1)\m{a}$に一致します．つまり，$-\m{a}=(-1)\m{a}$ですね．

$\m{a},\m{b}\in\R^n\setminus\{\m{0}\}$が平行であるとは，$k\m{a}=\m{b}$をみたす$k\in\R$が存在することをいう．

$\m{a},\m{b}\in\R^{n}$が平行であるとは，図形的には$\m{a}$の伸び縮みだけで$\m{b}$に一致させられることをいうわけですね．

ただし，$k<0$の場合には$\m{a}$と$\m{b}$は逆向きになります(すなわち，逆向きに伸び縮みさせると考えます)．

なお，複素ベクトルの場合にも同様に定義されます．よって，$\m{a}:=\bmat{1\\2\\3},\m{b}:=\bmat{2\\4\\6},\m{c}:=\bmat{-i\\-2i\\-3i}\in\C^{3}$は

$\begin{align*} 2\m{a}=\m{b},\quad i\m{a}=\m{b},\quad 2i\m{c}=\m{b} \end{align*}$

を満たすので，$\m{a}$, $\m{b}$, $\m{c}$は全て互いに平行となります．

行列とベクトルの積

さきほど，連立方程式$\begin{cases}y_1=x_1+2x_2+3x_3\\y_2=4x_1+5x_2+6x_3\end{cases}$を

$\begin{align*} \bmat{y_1\\y_2}=\bmat{1&2&3\\4&5&6}\bmat{x_1\\x_2\\x_3} \end{align*}$

と表すと述べました．実はこの式の右辺は

行列$\bmat{1&2&3\\4&5&6}$
ベクトル$\bmat{x_1\\x_2\\x_3}$

の積と考えます．

行列とベクトルの積を一般に以下のように定義します．

$\m{x}=[x_{1},\dots,x_{n}]^{T}\in\R^n$, $A=(a_{ij})\in\Mat_{mn}(\R)$に対して，$\m{x}$に左から$A$をかけた積$A\m{x}$を

$\begin{align*} A\m{x} =&\bmat{a_{11}&\dots&a_{1n}\\\vdots&\ddots&\vdots\\a_{m1}&\dots&a_{mn}}\bmat{x_{1}\\\vdots\\x_{n}} \\:=&\bmat{a_{11}x_{1}+\dots+a_{1n}x_{n}\\\vdots\\a_{m1}x_{1}+\dots+a_{mn}x_{n}} \end{align*}$

で定義する．

例えば，

$\begin{align*} \bmat{1&2&3\\4&5&6}\bmat{x\\y\\z} =\bmat{x+2y+3z\\4x+5y+6z},\quad \bmat{1&2\\3&4\\5&6}\bmat{a\\b} =\bmat{a+2b\\3a+4b\\5a+6b} \end{align*}$

ですね．

行列の積

次に行列の積を定義しますが，どのように定義するのが良いか考えましょう．

行列とベクトルの積については，定義から

$B\in\Mat_{nm}(\R)$を左から$\m{x}\in\R^n$にかけて$B\m{x}\in\R^m$
さらに左から$A\in\Mat_{m\ell}(\R)$をかけると$A(B\m{x})\in\R^{\ell}$

となります：

$\begin{align*} \begin{matrix} \R^n & \to & \R^m & \to & \R^\ell \\ \rotatebox[origin=c]{90}{$\in$} & & \rotatebox[origin=c]{90}{$\in$} & & \rotatebox[origin=c]{90}{$\in$} \\ \m{x} & \mapsto & B\m{x} & \mapsto & A(B\m{x}) \end{matrix}. \end{align*}$

さて，ここで行列$A$と$B$の積$AB$をするとき，結合法則$A(B\m{x})=(AB)\m{x}$が成り立っていて欲しいと思うのは自然なことですね．

たとえば，$A=\bmat{2&2\\-3&1}$, $B=\bmat{-2&0\\3&1}$, $\m{x}=\bmat{x\\y}$の場合を考えると，

$\begin{align*} A(B\m{x}) =&A\bra{\bmat{-2&0\\3&1}\bmat{x\\y}} =A\bmat{-2x\\3x+y} \\=&\bmat{2&2\\-3&1}\bmat{-2x\\3x+y} =\bmat{2(-2x)+2(3x+y)\\-3(-2x)+(3x+y)} \\=&\bmat{2x+2y\\9x+y} =\bmat{2&2\\9&1}\bmat{x\\y} =\bmat{2&2\\9&1}\m{x} \end{align*}$

となるので，$AB=\bmat{2&2\\9&1}$と定義されていれば，結合法則$A(B\m{x})=(AB)\m{x}$が成り立ちます．

このように，行列の積が結合法則をもつように定義しようとすると，行列の積の定義は以下のようになります．

$A=(a_{ij})\in\Mat_{mn}(\R)$, $B=(b_{ij})\in\Mat_{n\ell}(\R)$とする．このとき，積$AB$を以下で定義する．

$\begin{align*} AB :=\bra{\sum_{k=1}^{n} a_{ik}b_{kj}}_{1\leqq i\leqq m,1\leqq j\leqq \ell} =\bmat{ \sum_{k=1}^{n} a_{1k}b_{k1}&\dots&\sum_{k=1}^{n} a_{1k}b_{k\ell}\\ \vdots&\ddots&\vdots\\ \sum_{k=1}^{n} a_{mk}b_{k1}&\dots&\sum_{k=1}^{n} a_{mk}b_{k\ell} } \end{align*}$

たとえば，$A=\bmat{1&2\\3&6}$, $B=\bmat{-1&3\\1&0}$, $C=\bmat{2&0\\-1&0}$とすると，

$\begin{align*} &AB =\bmat{1\cdot(-1)+2\cdot1&1\cdot3+2\cdot0\\3\cdot(-1)+6\cdot1&3\cdot3+6\cdot0} =\bmat{1&3\\3&9}, \\&BA =\bmat{(-1)\cdot1+3\cdot3&(-1)\cdot2+3\cdot6\\1\cdot1+0\cdot3&1\cdot2+0\cdot6} =\bmat{8&16\\1&2}, \\&AC =\bmat{1\cdot2+2\cdot(-1)&1\cdot0+2\cdot0\\3\cdot2+6\cdot(-1)&3\cdot0+6\cdot0} =\bmat{0&0\\0&0} \end{align*}$

となります．

さて，この例から$AB\neq BA$, $AC=O$となることが分かります．このように，

行列の積は可換(交換可能)とは限らないし，
行列の積が零行列であってもどちらかが零行列であるとは限らない

ということに注意してください．

行列の積の表し方

$A=(a_{ij})\in\Mat_{mn}(\R)$, $B=(b_{ij})\in\Mat_{n\ell}(\R)$に対して，積$AB$を次の命題の形で表すことはとてもよくあります．

$A=(a_{ij})\in\Mat_{mn}(\R)$, $B=(b_{ij})\in\Mat_{n\ell}(\R)$を

$\begin{align*} A=\bmat{\m{a}_1\\\vdots\\\m{a}_m},\quad B=[\m{b}_1,\dots,\m{b}_{\ell}] \end{align*}$

とすると，以下のいずれも積$AB$に等しい．

$\bmat{\m{a}_1\m{b}_1&\dots&\m{a}_1\m{b}_\ell\\\vdots&\ddots&\vdots\\\m{a}_m\m{b}_1&\dots&\m{a}_m\m{b}_\ell}$
$[A\m{b}_1,\dots,A\m{b}_\ell]$
$\bmat{\m{a}_{1}B\\\vdots\\\m{a}_{m}B}$

証明を表示

(1)　任意の$i=1,\dots,m$に対して，

$\begin{align*} \m{a}_{i}=[a_{i1},\dots,a_{in}],\quad \m{b}_{i}=\bmat{b_{1i}\\\vdots\\b_{ni}} \end{align*}$

だから，

$\begin{align*} \m{a}_{i}\m{b}_{j} =a_{i1}b_{1j}+\dots+a_{in}b_{nj} =\sum_{k=1}^{n}a_{ik}b_{kj} \end{align*}$

であり，定義からこれは積$AB$の$(i,j)$成分だから，

$\begin{align*} AB=\bmat{\m{a}_1\m{b}_1&\dots&\m{a}_1\m{b}_\ell\\ \vdots&\ddots&\vdots\\ \m{a}_m\m{b}_1&\dots&\m{a}_m\m{b}_\ell} \end{align*}$

が成り立つ．

(2)　(1)の等式の第$j$列は

$\begin{align*} \bmat{\m{a}_1\m{b}_j\\\vdots\\\m{a}_m\m{b}_j} =\bmat{\m{a}_1\\\vdots\\\m{a}_m}\m{b}_j =A\m{b}_j \end{align*}$

だから，積$AB$は

$\begin{align*} AB=[A\m{b}_1,\dots,A\m{b}_l] \end{align*}$

と表せる．

(3)　同様に，(1)の等式の第$i$列は

$\begin{align*} [\m{a}_i\m{b}_1,\dots,\m{a}_i\m{b}_l] =\m{a}_{i}[\m{b}_1,\dots,\m{b}_l] =\m{a}_{i}B \end{align*}$

だから，積$AB$は

$\begin{align*} AB=\bmat{\m{a}_{1}B\\\vdots\\\m{a}_{m}B} \end{align*}$

と表せる．

逆行列

最後に逆行列を説明します．

逆行列は実数でいう逆数に相当する概念で，以下のように定義されます．

$A\in\Mat_n(\R)$に対し，

$\begin{align*} AB=BA=I \end{align*}$

をみたす$B\in\Mat_n(\R)$が存在するとき，$B$は$A$の逆行列 (inverse matrix)であるといい，$B$を$A^{-1}$と表す．また，逆行列をもつ行列は正則 (regular)であるという．

「逆行列は実数でいう逆数の概念」であると書きましたが，実数の場合には０でなければ逆数を持ちますが，行列の場合には零行列$O$でなくても逆行列を持たないことがあるという点は大きな違いです．

例えば，$\bmat{1&2\\2&4}$は逆行列を持たないことがのちの記事で(それほど難しくなく)分かります．

他にも，全ての成分が０である行や列をもつ行列なども正則行列になり得ません．

正則行列はどの行，どの列も零ベクトルでない．

証明を表示

背理法により示す．正則行列$A=[\m{a}_{1},\dots,\m{a}_{n}]$の第$k$列$\m{a}_{k}$が$\m{0}$であると仮定し，$A$の逆行列を$B$とすると

$\begin{align*} I=&BA \\=&[B\m{a}_{1},\dots,B\m{a}_{n}] \\=&[B\m{a}_{1},\dots,B\m{a}_{k-1},\m{0},B\m{a}_{k+1},\dots,B\m{a}_{n}] \end{align*}$

であるが，$I$の第$k$行は零ベクトルでないから，これは矛盾である．

よって，過程が誤りで$A$のどの列も零ベクトルでない．

行に関しては，$A$を行ベクトルで表して積$AB$を考えれば，同様に従う．

さて，正則行列の積について，次が成り立ちます．

正則な$A,B\in\Mat_{n}(\R)$に対して，積$AB$は正則であり，$(AB)^{-1}=B^{-1}A^{-1}$が成り立つ．

証明を表示

$AA^{-1}=A^{-1}A=BB^{-1}=B^{-1}B=I$より

$\begin{align*} &(AB)(B^{-1}A^{-1}) =A(BB^{-1})A^{-1} =AIA^{-1} =AA^{-1} =I, \\&(B^{-1}A^{-1})(AB) =B^{-1}(A^{-1}A)B =B^{-1}IB =B^{-1}B =I \end{align*}$

が成り立つから，$(AB)^{-1}=B^{-1}A^{-1}$を得る．

掃き出し法

たとえば

$\begin{align*} \begin{cases}x+y+z=2\\x+2y+3z=4\end{cases} \end{align*}$

のように，いくつかの１次方程式を同時に満たす複数の未知数に関する方程式を連立１次方程式といいます．

連立１次方程式の解法として加減法がありますが，加減法は行列を考えることによって本質的に全く同じことができ，この行列を用いた解法を掃き出し法といいます．

加減法が分かっていれば掃き出し法は簡単に理解できる解法ですが，線形代数の理論は掃き出し法がベースにあるといってもよいくらい掃き出し法は重要な考え方です．

次の記事では，この掃き出し方の考え方を説明します．

「線形代数学の基本」の一連の記事はこちら

【線形代数の初学者のための道案内｜線形代数のイメージを知る】

・行列と数ベクトル
【線形代数１｜行列の計算の基本！行列の積はなぜこうなる？】
【線形代数２｜連立１次方程式の掃き出し法と行列の基本変形】←次の記事
【線形代数３｜正則の条件を簡単に！基本変形と行列の積の話】
【線形代数４｜行列のランクと，行列が逆行列をもつための条件】
【線形代数５｜連立１次方程式が解をもつ条件と解の自由度】
【線形代数６｜線形独立のイメージと線形独立であるための条件】

参考文献

線型代数入門

[齋藤正彦著/東京大学出版会]

線形代数の教科書として半世紀に渡って売れ続けている超ロングセラーの教科書です．

発刊されてから本書の内容の流れが線形代数の教科書のスタンダードとなったほど，日本の線形代数の指導にインパクトを与えた名著です．

その証拠に，著者の齋藤正彦氏は本書で日本数学会出版賞を受賞しています．

「線形代数をとりあえず使えるようにするための教科書」ではなく「線形代数を理解するための教科書」のため，論理的に非常に詳しく書かれているのが特徴です．

また，テキストのレベルとしては少なくとも理論系(特に数学系)の学部生であれば，確実に理解しておきたい程度のものとなっています．

Amazon 楽天市場

なお，本書については，以下の記事で書評としてまとめています．

【書評｜線型代数入門(齋藤正彦著，東京大学出版会)】

本書の良い点や気になる点，オススメの使い方などをレビューしています．これから理論系として数学を扱う人は，是非とも持っておきたい１冊です．