線形独立性の考え方を例題から解説｜ランクとの関係も解説

ベクトルの線形独立性は線形代数学のさまざまな場面に現れる重要な概念です．

例えば，２次列ベクトル$\bmat{2\\1}$, $\bmat{-1\\1}$が

\begin{align*}c_1\bmat{2\\1}+c_2\bmat{-1\\1}=\bmat{0\\0}\end{align*}

をみたすとしましょう（$c_1$, $c_2$は定数）．この$c_1$, $c_2$は各成分ごとで両辺を比較して

\begin{align*}\begin{cases}2c_1-c_2=0\\c_1+c_2=0\end{cases}\end{align*}

を満たすので，この連立１次方程式を解いて$(c_1,c_2)=(0,0)$となります．

このことを言葉で説明すれば，$\bmat{2\\1}$, $\bmat{-1\\1}$をうまく定数倍して足し合わせて$\bmat{0\\0}$をつくるには係数を全て０にするしかないということになります．

確かに図形的にも，０をかけて$\bmat{2\\1}$, $\bmat{-1\\1}$をともに零ベクトルにして足し合わせないと，零ベクトルにはならなさそうですね．

このように「ベクトルの定数倍をうまく足し合わせて零ベクトル$\m{0}$をつくるには係数を全て０にするしかない」とき，そのベクトルたちは線形独立であるといいます．

この記事では

線形結合の定義と具体例
線形関係の定義と具体例
線形独立の定義と具体例
線形独立性と行列のランクの関係

を順に説明します．

なお，この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが，複素行列など一般の体を成分とする行列・ベクトルに対しても同様です．

「線形代数学の基本」の一連の記事

行列と列ベクトル

行列式

$\R^n$の部分空間と基底

正方行列の対角化

線形結合の定義と具体例

列ベクトルの線形独立性を定義するために，まずは線形結合を定義しておきましょう．

列ベクトル$\m{a}_1,\m{a}_2,\dots,\m{a}_r$に対して，スカラー$c_1,c_2,\dots,c_r$を用いて

\begin{align*}c_1\m{a}_1+c_2\m{a}_2+\dots+c_r\m{a}_r\end{align*}

と表せるベクトルを$\m{a}_1,\dots,\m{a}_r$の線形結合（linear combination）という．

つまり，ベクトルを定数倍して足し合わせてできるベクトルを線形結合というわけですね．

具体例１（２次列ベクトル）

２次列ベクトル$\bmat{1\\0}$, $\bmat{1\\1}$を考えましょう．それぞれ$-2$倍，$3$倍してできるベクトルを足し合わせると

\begin{align*}(-2)\bmat{0\\1}+3\bmat{1\\1}=\bmat{3\\1}\end{align*}

となりますね．よって，$\bmat{3\\1}$は$\bmat{1\\0}$, $\bmat{1\\1}$の線形結合のひとつです．

他にも

\begin{align*}3\bmat{0\\1}+1\bmat{1\\1}=\bmat{1\\4},\quad
0\bmat{0\\1}+0\bmat{1\\1}=\bmat{0\\0}\end{align*}

などとなるので，$\bmat{1\\4}$, $\bmat{0\\0}$も$\bmat{1\\0}$, $\bmat{1\\1}$の線形結合です．

係数を変えればさまざまなベクトルができあがります．このようにできあがるベクトルを全て線形結合というわけですね．

具体例２（３次列ベクトル）

列ベクトルの次数が変わっても考え方は同じです．

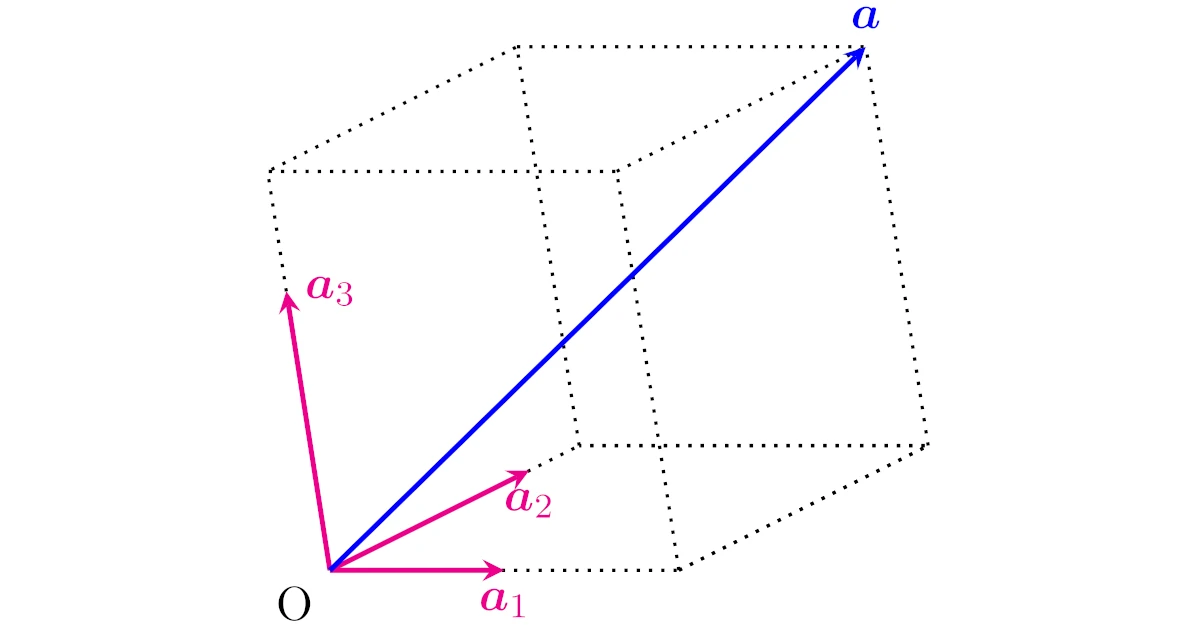
３次列ベクトル$\bmat{1\\1\\0}$, $\bmat{2\\3\\2}$, $\bmat{1\\2\\1}$の線形結合としては，例えば

\begin{align*}2\bmat{1\\1\\0}+(-1)\bmat{2\\3\\2}+1\bmat{1\\2\\1}=\bmat{1\\1\\-1}\end{align*}

が挙げられますね．この他にも係数を変えればさまざまなベクトルとなり，それらも$\bmat{1\\1\\0}$, $\bmat{2\\3\\2}$, $\bmat{1\\2\\1}$の線形結合ですね．

それぞれのベクトルを$\m{a}_1$, $\m{a}_2$, $\m{a}_3$とおくと，これらの線形結合$\m{a}$は下図のようになりますね．

つまり，$\m{a}_1$, $\m{a}_2$, $\m{a}_3$をうまく伸び縮みさせて足してつくることのできるベクトルが線形結合というわけですね．

具体例３（線形結合としての零ベクトル）

任意の$n$次列ベクトル$\m{a}_1,\dots,\m{a}_r$に対して，係数を全て０にすれば

\begin{align*}0\cdot\m{a}_1+\dots+0\cdot\m{a}_r=\m{0}_n\end{align*}

と零ベクトル$\m{0}_n$になりますね．

このように，零ベクトルはどのようなベクトルたちの線形結合としても表すことができますね．

線形関係の定義と具体例

いまの線形結合の例３で見たように，零ベクトル$\m{0}$はどんなベクトルたちの線形結合としても表すことができます．

そこで，次のように線形関係というものを定義します．

列ベクトル$\m{a}_1,\m{a}_2,\dots,\m{a}_r$の線形結合で零ベクトル$\m{0}$を表した等式

\begin{align*}\m{0}=c_1\m{a}_1+c_2\m{a}_2+\dots+c_r\m{a}_r\end{align*}

を$\m{a}_1,\m{a}_2,\dots,\m{a}_r$の線形関係という．また，

係数が全て０の線形関係を自明な線形関係（trivial linear relation）
少なくとも１つの係数が０でない線形関係を非自明な線形関係（nontrivial linear relation）

という．

具体例１（自明な線形関係しかもたない例）

この記事の冒頭の２次列ベクトル$\bmat{2\\1}$, $\bmat{-1\\1}$の線形関係

\begin{align*}\bmat{0\\0}=c_1\bmat{2\\1}+c_2\bmat{-1\\1}\end{align*}

を考えると，各成分ごとで両辺を比較して

\begin{align*}\begin{cases}2c_1-c_2=0\\c_1+c_2=0\end{cases}\end{align*}

となるので，この連立１次方程式を解いて$(c_1,c_2)=(0,0)$となります．

よって，$\bmat{2\\1}$, $\bmat{-1\\1}$の線形結合で零ベクトル$\bmat{0\\0}$をつくるには，係数を全て０にするしかないということになりますね．

言い換えれば，$\bmat{2\\1}$, $\bmat{-1\\1}$は自明な線形結合しかもたないということですね．

のちに定義するように，このことを$\bmat{2\\1}$, $\bmat{-1\\1}$が線形独立であるといいます．

具体例２（非自明な線形関係をもつ例）

２次列ベクトル$\bmat{2\\1}$, $\bmat{4\\2}$の線形関係

\begin{align*}\bmat{0\\0}=c_1\bmat{2\\1}+c_2\bmat{4\\2}\end{align*}

を考えると，各成分ごとで両辺を比較して

\begin{align*}\begin{cases}2c_1+4c_2=0\\c_1+2c_2=0\end{cases}\end{align*}

となるので，たとえば$(c_1,c_2)=(2,-1)$がとれます．

よって，非自明な線形関係

\begin{align*}\bmat{0\\0}=2\bmat{2\\1}+(-1)\bmat{4\\2}\end{align*}

が成り立つことが分かります．

もちろん自明な線形関係$\bmat{0\\0}=0\bmat{2\\1}+0\bmat{4\\2}$も成り立ちますが，この例で大切なことは$\bmat{2\\1}$, $\bmat{4\\2}$に非自明な線形関係をもつという点です．

線形独立性の定義と具体例

それでは本題の列ベクトルの線形独立性を定義し，具体例を考えましょう．

列ベクトル$\m{a}_1,\m{a}_2,\dots,\m{a}_r$の線形関係が自明な線形関係のみであるとき，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$は線形独立（linearly independent）であるという．

一方，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$が線形独立でないとき，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$は線形従属（linearly dependent）であるという．

言い換えると，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$の線形結合で零ベクトル$\m{0}$をつくるためには係数を全て０とするしかないとき，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$は線形独立であるというわけですね．

具体例１（線形独立の例）

線形結合の具体例１で見たように，２次列ベクトル$\bmat{2\\1}$, $\bmat{-1\\1}$の線形関係は自明な線形関係

\begin{align*}\bmat{0\\0}=0\bmat{2\\1}+0\bmat{-1\\1}\end{align*}

しかあり得ないのでしたから，列ベクトル$\bmat{2\\1}$, $\bmat{-1\\1}$は線形独立です．

具体例２（線形従属の例）

２次列ベクトル$\bmat{2\\1}$, $\bmat{4\\2}$は非自明な線形関係

\begin{align*}\bmat{0\\0}=2\bmat{2\\1}+(-1)\bmat{4\\2}\end{align*}

をもちましたから，列ベクトル$\bmat{2\\1}$, $\bmat{4\\2}$は線形従属です．

具体例３（１個のベクトル）

２次列ベクトル$\bmat{2\\1}$の線形関係

\begin{align*}c_{1}\bmat{2\\1}=\bmat{0\\0}\end{align*}

を考えると，各成分ごとで両辺を比較して$c_1=0$となるしかありませんから，列ベクトル$\bmat{2\\1}$は線形独立です．

この例からも分かるように，零ベクトルでない１個のみのベクトルは必ず線形独立ですね．

具体例４（３次列ベクトル）

列ベクトルの次数が変わっても考え方は同じです．

３次列ベクトル$\bmat{1\\0\\0}$, $\bmat{0\\1\\0}$, $\bmat{0\\0\\1}$の線形関係

\begin{align*}c_1\bmat{1\\0\\0}+c_2\bmat{0\\1\\0}+c_3\bmat{0\\0\\1}=\bmat{0\\0\\0}\end{align*}

を考えると，各成分ごとで両辺を比較して$c_1=0$となるしかありませんから，列ベクトル$\bmat{1\\0\\0}$, $\bmat{0\\1\\0}$, $\bmat{0\\0\\1}$は線形独立です．

線形独立性とランクの関係

次に，線形独立性と行列のランクの関係を説明します．

斉次連立１次方程式の解

前回の記事では次の定理を（２つに分けて）証明しました．

$n\times r$行列$A$と$n$次列ベクトル$\m{c}$に対し，次は同値である．

$\rank{A}=\rank{[A,\m{c}]}$が成り立つ
$\m{x}$の連立１次方程式$A\m{x}=\m{c}$が解をもつ

さらに，次も同値である．

$r=\rank{A}=\rank{[A,\m{c}]}$が成り立つ
$\m{x}$の連立１次方程式$A\m{x}=\m{c}$の解は一意である

斉次連立１次方程式$A\m{x}=\m{0}$を考えると，$\rank{A}=\rank{[A,\m{0}]}$ですからこの定理の前半から必ず解をもちます．

$\m{x}=\m{0}$のとき必ず等式$A\m{x}=\m{0}$が成り立つ（自明解$\m{x}=\m{0}$をもつ）ことからも解をもつことは分かりますね．

つまり，斉次連立１次方程式$A\m{x}=\m{0}$では，この定理の前半は常に満たされるわけですね．

したがって，この定理の後半から係数行列である$n\times r$行列$A$のランクが$r=\rank{A}$が成り立てば斉次連立１次方程式$A\m{x}=\m{0}$の解は一意となりますから，解は常に存在することが分かっている自明解$\m{x}=\m{0}$のみであることになります．

よって，斉次連立１次方程式$A\m{x}=\m{0}$に対して，この定理は次のように言い換えることができますね．

$n\times r$行列$A$に対し，次は同値である．

$\rank{A}=r$が成り立つ
$\m{x}$の連立方程式$A\m{x}=\m{0}$が自明解$\m{x}=\m{0}$のみもつ

線形独立性とランク

列ベクトル$\m{a}_1,\m{a}_2,\dots,\m{a}_r$に対して$A=[\m{a}_1,\dots,\m{a}_r]$とおくと，連立１次方程式$A\m{x}=\m{0}$は

\begin{align*}x_1\m{a}_1+x_2\m{a}_2+\dots+x_r\m{a}_r=\m{0}\end{align*}

となりますね．ただし，$\m{x}=\bmat{x_1\\\vdots\\x_n}$です．このことから，

斉次連立１次方程式$A\m{x}=\m{0}$の解が$\m{x}=\m{0}$のみ
$x_1\m{a}_1+x_2\m{a}_2+\dots+x_r\m{a}_r=\m{0}$を満たす$x_1,x_2,\dots,x_r$は$x_1=x_2=\dots=x_r=0$のみ

は同値ということが分かります．よって，いまの系はさらに次のように書き直すことができますね．

$n\times r$行列$A=[\m{a}_1,\dots,\m{a}_r]$に対し，次は同値である．

$\rank{A}=r$が成り立つ
$\m{a}_1,\dots,\m{a}_r$は線形独立である

線形独立性と正則性

とくに$n$次正方行列$A$に対して，

$A$は正則行列
$\rank{A}=n$

は同値でしたから，さらに次の系が従いますね．

$n$次正方行列$A=[\m{a}_{1},\dots,\m{a}_{n}]$に対して，次は同値である．

$A$は正則行列である
$\m{a}_{1},\dots,\m{a}_{n}$は線形独立である

線形独立性の考え方を例題から解説｜ランクとの関係も解説

線形代数学の参考文献

大学教養線形代数（加藤文元著）

手を動かしてまなぶ線形代数（藤岡敦著）