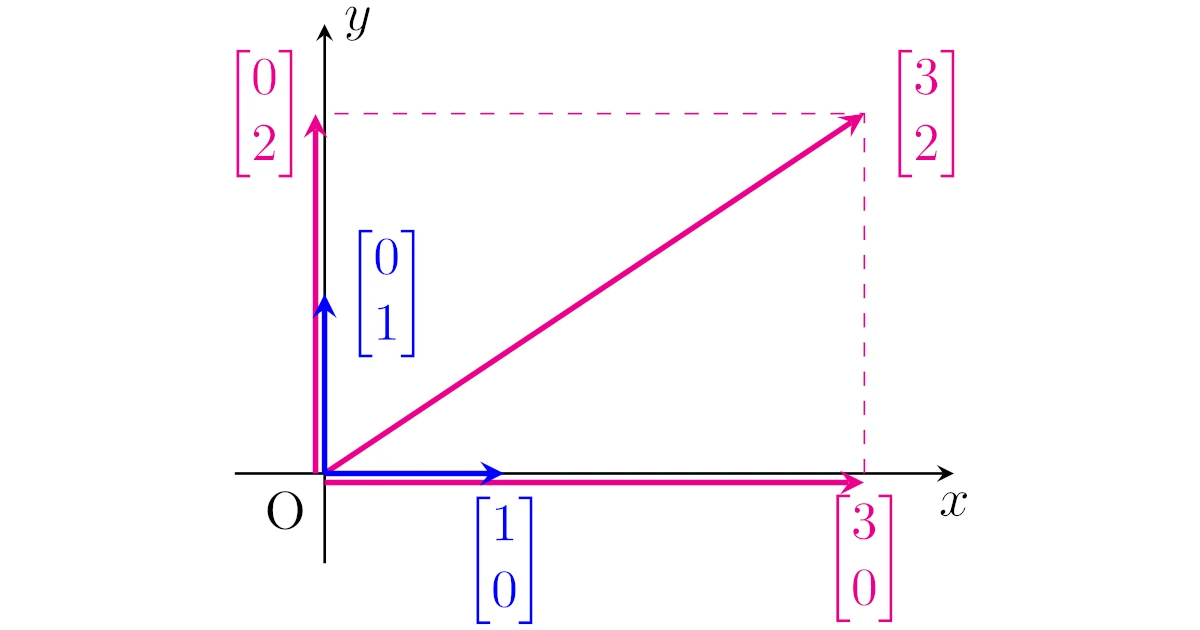
例えば，$\bmat{3\\2}\in\R^2$は２つのベクトル$\bmat{1\\0}$と$\bmat{0\\1}$の線形結合（和とスカラー倍）で
\begin{align*}\bmat{3\\2}=3\bmat{1\\0}+2\bmat{0\\1}\end{align*}
と表すことができますね．また，このときの係数は３，２とする以外にありえません．
一般に任意の$\bmat{a\\b}\in\R^2$に対して
- $\bmat{a\\b}$は$\bmat{1\\0}$と$\bmat{0\\1}$の線形結合で表せる
- その線形結合の表し方は１通りしかない
という２つの性質が成り立ちます．
これら２つの性質を満たすベクトルの組を$\R^2$の基底といい，より一般に$\R^n$の部分空間に対しても基底が定義されます．
この記事では
- 列ベクトルの線形独立性（復習）
- 生成される部分空間の定義と具体例
- $\R^n$の部分空間の基底の定義と具体例
を順に解説します．
なお，特に断らない限り以下では実行列・実ベクトルを扱うことにしますが，複素行列など一般の体を成分とする行列・ベクトルに対しても同様です．
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
線形代数学の参考文献
以下は線形代数学に関するオススメの教科書です．
大学教養 線形代数（加藤文元 著）
数学科など理論系の学生向けの線形代数の入門書です．平易な例から丁寧に説明されています．
手を動かしてまなぶ 線形代数（藤岡敦 著）
理論と演習のバランスをとりながら勉強したい人にオススメの入門書です．
列ベクトルの線形独立性（復習）
まずはベクトルの線形独立性を復習し，基底を理解するのに必要な性質を説明します．
自明な線形結合のみもつとき線形独立という
零ベクトル$\m{0}\in\R^{n}$はどんなベクトルたち$\m{a}_1,\m{a}_2,\dots,\m{a}_r\in\R^n$に対しても，
\begin{align*}\m{0}=0\m{a}_1+0\m{a}_2+\dots+0\m{a}_r\end{align*}
と線形結合で表すことができますが，これ以外の係数で$\m{0}$を$\m{a}_1,\m{a}_2,\dots,\m{a}_r$の線形結合で表せるかどうか一般には分かりません．
このことをもとに線形独立性は次のように定義されるのでした．
$\m{a}_1,\m{a}_2,\dots,\m{a}_r\in\R^{n}$が自明な線形関係のみもつとき，すなわち
\begin{align*}x_1\m{a}_1+x_2\m{a}_2+\dots+x_r\m{a}_r=\m{0}\end{align*}
を満たす$x_1,x_2,\dots,x_r$が$x_1=x_2=\dots=x_r=0$に限るとき，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$は線形独立（linearly independent）であるという．
一方，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$が線形独立でないとき，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$は線形従属（linearly dependent）であるという．
線形独立と同値な重要性質
この記事のメインテーマの基底を説明するために，線形独立性に関する次の性質を理解しておきましょう．
$\m{a}_1,\m{a}_2,\dots,\m{a}_r\in\R^n$を考える．このとき，次は同値である．
- $\m{a}_1,\m{a}_2,\dots,\m{a}_r$が線形独立である
- $c_1\m{a}_1+c_2\m{a}_2+\dots+c_r\m{a}_r=d_1\m{a}_1+d_2\m{a}_2+\dots+d_r\m{a}_r$が成り立てば$c_k=d_k$（$k=1,2,\dots,r$）が成り立つ．
言い換えれば，$\m{a}_1,\m{a}_2,\dots,\m{a}_r\in\R^n$が線形独立でひとつのベクトルを表すとき，係数のとり方は一意だということですね．
(1)⇒(2)の証明
(1)が成り立つとする．また，
\begin{align*}c_1\m{a}_1+c_2\m{a}_2+\dots+c_r\m{a}_r=d_1\m{a}_1+d_2\m{a}_2+\dots+d_r\m{a}_r\end{align*}
が成り立つとする．このとき，
\begin{align*}(c_1-d_1)\m{a}_1+(c_2-d_2)\m{a}_2+\dots+(c_r-d_r)\m{a}_r=\m{0}\end{align*}
だから，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$の線形独立性と併せて$c_k-d_k=0$なので$c_k=d_k$が成り立つ（$k=1,2,\dots,r$）．
(2)⇒(1)の証明
(2)が成り立つとする．また，$c_1\m{a}_1+c_2\m{a}_2+\dots+c_r\m{a}_r=0$が成り立つとする．このとき，
\begin{align*}c_1\m{a}_1+c_2\m{a}_2+\dots+c_r\m{a}_r=0\m{a}_1+0\m{a}_2+\dots+0\m{a}_r\end{align*}
が成り立つので，(2)より$c_k=0$が成り立つ（$k=1,2,\dots,r$）．よって，$\m{a}_1,\m{a}_2,\dots,\m{a}_r$は線形独立である
いまの定理は高校数学で学ぶ「零ベクトルでなく平行でない$\ve{a}$, $\ve{b}$に対して，$k\ve{a}+\ell\ve{b}=k’\ve{a}+\ell’\ve{b}$なら$k=k’$, $\ell=\ell’$が成り立つ」の一般化ですね．
生成される部分空間の定義と具体例
基底の定義を理解するには，いま説明した線形独立性と生成される部分空間が重要です．
生成される部分空間は線形結合で表せるベクトル全部の空間
生成される部分空間を定義するために，まずは次の補題を示しておきましょう．
$\m{a}_1,\dots,\m{a}_r\in\R^n$とする．このとき，部分集合
\begin{align*}V=\set{c_1\m{a}_1+\dots+c_r\m{a}_r}{c_1,\dots,c_r\in\R}\end{align*}
は$\R^n$の部分空間となる．
$V$が$\R^n$の部分集合で空でないことは明らか．任意に$k\in\R$と$\m{a},\m{b}\in V$をとる．このとき，$c_p,d_p\in\R$（$p=1,\dots,r$）を用いて
\begin{align*}\m{a}=c_1\m{a}_1+\dots+c_r\m{a}_r,\quad
\m{b}=d_1\m{a}_1+\dots+d_r\m{a}_r\end{align*}
と表せるから，
\begin{align*}\m{a}+\m{b}&=(c_1\m{a}_1+\dots+c_r\m{a}_r)+(d_1\m{a}_1+\dots+d_r\m{a}_r)
\\&=(c_1+d_1)\m{a}_1+\dots+(c_r+d_r)\m{a}_r\in V,
\\k\m{a}&=k(c_1\m{a}_1+\dots+c_r\m{a}_r)
\\&=(kc_1)\m{a}_1+\dots+(kc_r)\m{a}_r\in V\end{align*}
この部分空間は重要な部分空間で次のように呼ばれます．
$\m{a}_1,\dots,\m{a}_r\in\R^n$とする．このとき，$\R^n$の部分空間
\begin{align*}V=\set{c_1\m{a}_1+\dots+c_r\m{a}_r}{c_1,\dots,c_r\in\R}\end{align*}
は$\m{a}_1,\dots,\m{a}_r$によって張られる部分空間（span）または生成される部分空間（generated space）といい，$\spn{(\m{a}_1,\dots,\m{a}_r)}$などと表す．
言葉で説明すれば，$\spn{(\m{a}_1,\dots,\m{a}_r)}$は$\m{a}_1,\dots,\m{a}_r$の線形結合で表されるベクトル全部からなる部分空間ということができますね．
具体例１（１つの列ベクトルで生成される空間）
$\R^2$において$V=\spn{\bra{\bmat{2\\1}}}$とおくと，
\begin{align*}V=\set{t\bmat{2\\1}}{t\in\R}\end{align*}
なので，$\bmat{2\\1}$を伸び縮みさせてできる２次列ベクトル全部の集合が$V$ですね．
つまり，$\R^2$を$xy$空間とするとき，$V$は直線$y=\frac{1}{2}x$を表しますね．
具体例２（２つの列ベクトルで生成される空間）
$\R^2$において$V=\spn{\bra{\bmat{1\\0},\bmat{0\\1}}}$とおくと，
\begin{align*}V=\set{a\bmat{1\\0}+b\bmat{0\\1}}{a,b\in\R}
=\set{\bmat{a\\b}}{a,b\in\R}\end{align*}
なので，第１成分，第２成分が任意に動く２次列ベクトルの集合が$V$ですね．
これは$\R^2$全体に他なりませんから，$V=\R^2$と分かりますね．
具体例３（２つの列ベクトルで生成される空間）
$\m{e}_1=\bmat{1\\0\\0}$, $\m{e}_2=\bmat{0\\1\\0}$で$\m{e}_1,\m{e}_2\in\R^3$を定めます．
このとき，$V=\spn{(\m{e}_1,\m{e}_2)}$とおくと，
\begin{align*}V=\set{a\m{e}_1+b\m{e}_2}{a,b\in\R}=\set{\bmat{a\\b\\0}}{a,b\in\R}\end{align*}
なので，第１成分，第２成分が任意に動く３次列ベクトルの集合が$V$ですね．
つまり，$\R^3$を$xyz$空間とするとき，$V$は$xy$平面を表しますね．
$\R^n$の部分空間の基底の定義と具体例
それではこの記事のテーマの基底について，定義と具体例を説明します．
部分空間を張り線形独立なベクトルを基底という
$\R^n$の部分空間$V$に対して，$\m{a}_1,\dots,\m{a}_r\in V$が
- $V=\spn{(\m{a}_1,\dots,\m{a}_r)}$
- $\m{a}_1,\dots,\m{a}_r$が線形独立
を満たすとき，組$\anb{\m{a}_1,\dots,\m{a}_r}$を$V$の基底という．ただし，自明な部分空間$\{\m{0}_n\}$は基底をもたないとする．
つまり，
- $V$の全てのベクトルが$\m{a}_1,\dots,\m{a}_r$の線形結合で表せる
- その線形結合の表し方が一意である
の２つが成り立つときに，組$\anb{\m{a}_1,\dots,\m{a}_r}$を$V$の基底というわけですね．
基底は「組」なので順番が変わると異なる基底とみなします．例えば，$\anb{\m{a}_1,\m{a}_2}$が基底なら$\anb{\m{a}_2,\m{a}_1}$も基底ですが，これらは異なる基底とみなします．
しかし，しばらくは基底の順番を気にしなくても問題ありません．
具体例４（$\R^2$の標準基底）
$\m{e}_1,\m{e}_2\in\R^2$を$\m{e}_1:=\bmat{1\\0}$, $\m{e}_2:=\bmat{0\\1}$とすると，列ベクトルの組$\anb{\m{e}_1,\m{e}_2}$が$\R^2$の基底であることを示せ．
$\m{e}_1,\m{e}_2$が線形独立であり，$\m{e}_1,\m{e}_2$が$\R^2$を生成することを示せばよい．
$\m{e}_1,\m{e}_2$の線形独立性の証明
行列$[\m{e}_1,\m{e}_2]$のランクは
\begin{align*}\rank{[\m{e}_1,\m{e}_2]}=\rank{\bmat{1&0\\0&1}}=2\end{align*}
だから，$\m{e}_1,\m{e}_2$は線形独立である．
$\R^2=\spn{(\m{e}_1,\m{e}_2)}$の証明
集合の等号なので$\supset$と$\subset$を示せばよい．$\m{e}_1,\m{e}_2\in\R^2$より$\m{e}_1,\m{e}_2$の線形結合はすべて$\R^2$に属するから$\R^2\supset\spn{(\m{e}_1,\m{e}_2)}$である．また，任意の$\m{a}=\bmat{a\\b}\in\R^2$は
\begin{align*}\m{a}=a\m{e}_1+b\m{e}_2\end{align*}
と表せるので，$\m{a}\in\spn{(\m{e}_1,\m{e}_2)}$だから$\R^2\subset\spn{(\m{e}_1,\m{e}_2)}$である．したがって，$\R^2=\spn{(\m{e}_1,\m{e}_2)}$を得る．
一般に$\rank{[\m{a}_1,\m{a}_2,\dots,\m{a}_r]}=r$を満たす$\m{a}_1,\m{a}_2,\dots,\m{a}_r\in\R^n$は線形独立なのでした．
具体例５（$\R^2$の部分空間の基底）
$\m{a}\in\R^2$を$\m{a}:=\bmat{2\\1}$とすると，列ベクトルの組$\anb{\m{a}}$が$V=\spn{(\m{a})}$の基底であることを示せ．
$\anb{\m{a}}$を「組」と言うのは気持ち悪いかもしれませんが，２個以上の場合と言い方を統一して１個のベクトルでも「組」と言うのが普通です．
$V=\spn{(\m{a})}$は問題で与えられている．また，零ベクトルでない１個のベクトルは必ず線形独立だったから， $\m{a}$は線形独立である．
よって，$\anb{\m{a}}$は$V$の基底である．
一般に１個のベクトル$\m{a}$に対して，生成される部分空間$\spn{(\m{a})}$の基底として$\anb{\m{a}}$がとれます．
具体例６（$\R^3$の標準基底）
$\m{e}_1,\m{e}_2,\m{e}_3\in\R^3$を$\m{e}_1:=\bmat{1\\0\\0}$, $\m{e}_2:=\bmat{0\\1\\0}$, $\m{e}_3:=\bmat{0\\0\\1}$とすると，列ベクトルの組$\anb{\m{e}_1,\m{e}_2,\m{e}_3}$が$\R^3$の基底であることを示せ．
$\m{e}_1,\m{e}_2,\m{e}_3$が線形独立であり，$\m{e}_1,\m{e}_2,\m{e}_3$が$\R^3$を生成することを示せばよい．
$\m{e}_1,\m{e}_2,\m{e}_3$の線形独立性の証明
行列$[\m{e}_1,\m{e}_2,\m{e}_3]$のランクは
\begin{align*}\rank{[\m{e}_1,\m{e}_2,\m{e}_3]}
=\rank{\bmat{1&0&0\\0&1&0\\0&0&1}}
=3\end{align*}
だから，$\m{e}_1,\m{e}_2,\m{e}_3$は線形独立である．
$\R^3=\spn{(\m{e}_1,\m{e}_2,\m{e}_3)}$の証明
集合の等号なので$\supset$と$\subset$を示せばよい．$\m{e}_1,\m{e}_2,\m{e}_3\in\R^3$より$\R^3\supset\spn{(\m{e}_1,\m{e}_2,\m{e}_3)}$である．また，任意の$\m{a}\in\R^3$は
\begin{align*}\m{a}=a\m{e}_1+b\m{e}_2+c\m{e}_3\end{align*}
なので，$\m{a}\in\spn{(\m{e}_1,\m{e}_2,\m{e}_3)}$だから$\R^3\subset\spn{(\m{e}_1,\m{e}_2,\m{e}_3)}$である．したがって，$\R^3=\spn{(\m{e}_1,\m{e}_2,\m{e}_3)}$を得る．
例４と例６のように$\m{e}_k\in\R^n$を第$k$成分が１，第$k$成分以外が全て０の列ベクトルとすると，$\anb{\m{e}_1,\dots,\m{e}_n}$は$\R^n$の基底となります．
この基底を$\R^n$の標準基底といいます．
具体例７（$\R^3$の部分空間の基底）
$\m{a}_1,\m{a}_2\in\R^3$を$\m{a}_1:=\bmat{1\\2\\3}$, $\m{a}_2:=\bmat{-2\\0\\1}$とすると，列ベクトルの組$\anb{\m{a}_1,\m{a}_2}$が$V=\spn{(\m{a}_1,\m{a}_2)}$の基底であることを示せ．
$V=\spn{(\m{a}_1,\m{a}_2)}$は問題で与えられているから，あとは$\m{a}_1,\m{a}_2$の線形独立性を示せばよい．
\begin{align*}\rank{[\m{a}_1,\m{a}_2]}
=\rank{\bmat{1&-2\\2&0\\3&1}}
=\rank{\bmat{1&-2\\0&4\\0&7}}
=\rank{\bmat{1&0\\0&1\\0&0}}
=2\end{align*}
なので，$\m{a}_1,\m{a}_2$は線形独立である．
具体例８（$\R^3$の基底）
$\m{a}_1,\m{a}_2,\m{a}_3\in\R^3$を$\m{a}_1:=\bmat{1\\1\\1}$, $\m{a}_2:=\bmat{-2\\-2\\1}$, $\m{a}_3:=\bmat{0\\1\\-1}$とすると，列ベクトルの組$\anb{\m{a}_1,\m{a}_2,\m{a}_3}$が$\R^3$の基底であることを示せ．
$\m{a}_1,\m{a}_2,\m{a}_3$が線形独立であり，$\m{a}_1,\m{a}_2,\m{a}_3$が$\R^3$を生成することを示せばよい．
$\m{a}_1,\m{a}_2,\m{a}_3$の線形独立性の証明
\begin{align*}&\rank{[\m{a}_1,\m{a}_2,\m{a}_3]}
=\rank{\bmat{1&-2&0\\1&-2&1\\1&1&-1}}
\\&=\rank{\bmat{1&-2&0\\0&0&1\\0&3&-1}}
=\rank{\bmat{1&0&0\\0&1&0\\0&0&1}}
=3\end{align*}
なので，$\m{a}_1,\m{a}_2,\m{a}_3$は線形独立である．
$\R^3=\spn{(\m{a}_1,\m{a}_2,\m{a}_3)}$の証明
$\supset$と$\subset$を示せばよい．$\m{a}_1,\m{a}_2,\m{a}_3\in\R^3$より$\m{a}_1,\m{a}_2,\m{a}_3$の線形結合はすべて$\R^3$に属するから$\R^3\supset\spn{(\m{a}_1,\m{a}_2,\m{a}_3)}$である．
また，任意の$\m{a}\in\R^3$に対して，連立１次方程式
\begin{align*}&x\m{a}_1+y\m{a}_2+z\m{a}_3=\m{a}
\\&\iff[\m{a}_1,\m{a}_2,\m{a}_3]\m{x}=\m{a}\end{align*}
を考える．ただし，$\m{x}=\bmat{x\\y\\z}$である．
$\m{a}_1,\m{a}_2,\m{a}_3$は線形独立だったから$[\m{a}_1,\m{a}_2,\m{a}_3]$は正則行列なので解$\m{x}$が存在する．よって，$\m{a}\in\spn{(\m{a}_1,\m{a}_2,\m{a}_3)}$なので，$\R^3\subset\spn{(\m{a}_1,\m{a}_2,\m{a}_3)}$である．
したがって，$\R^3=\spn{(\m{a}_1,\m{a}_2,\m{a}_3)}$を得る．
例６の列ベクトルの組$\anb{\m{e}_1,\m{e}_2,\m{e}_3}$も$\R^3$の基底でした．
このように，同じ空間であっても全く別のベクトルからなる基底が存在することが分かりますね．
コメント