前回の記事では線形代数が「多変数バージョンの比例」を考える分野であることを説明し,線形代数の基本的な言葉である行列と列ベクトルがどのようなものかを説明しました.
実数で足し算・掛け算の計算が定まっているように,行列・列ベクトルにもいくつかの計算が定まっています.
この記事では
- 列ベクトルの計算(和・スカラー倍・行列倍)
- 行列の計算(和・スカラー倍・積)
- 行列のブロック分割と行列の積
を順に解説します.
なお,この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが,複素行列など一般の体を成分とする行列・ベクトルに対しても同様です.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
列ベクトルの計算(和・スカラー倍・行列倍)
単なる数を行列やベクトルと区別してスカラー(scalar)といいます.例えば,この記事では主に実行列・実ベクトルを扱うので,スカラーは実数です.
“scalar”は「梯子」を意味するラテン語の”scala”が語源です.「目盛り」や「縮尺」を意味する英語の”scale”(スケール)もラテン語の”scala”が語源となっています.このことから,行列やベクトルとは違い,スカラーは「量」を表すというニュアンスが感じられますね.
さて,まずは列ベクトルの計算として
- 列ベクトルの和
- 列ベクトルのスカラー倍
- 列ベクトルの行列倍
を定義します.
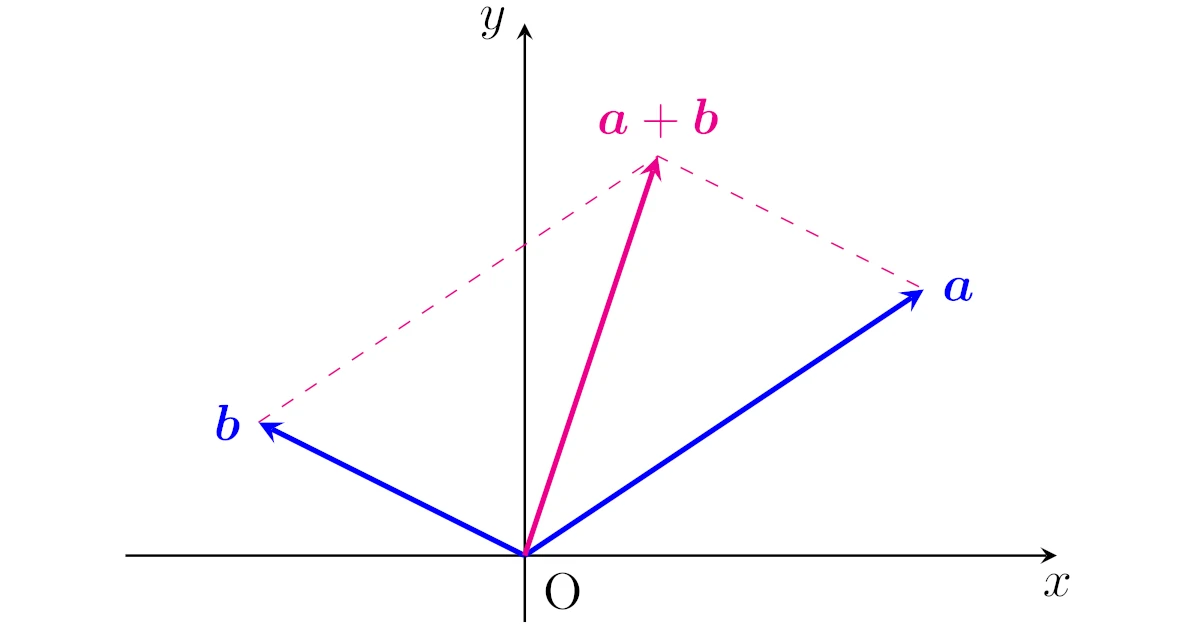
列ベクトルの和$\m{a}+\m{b}$の定義・具体例
列ベクトルの和は各成分ごとに和を計算してできる列ベクトルと定義されます.
列ベクトルの和の定義
$n$次列ベクトル$\m{a}=\bmat{a_1\\\vdots\\a_n}$, $\m{b}=\bmat{b_1\\\vdots\\b_n}$の和$\m{a}+\m{b}$を
\begin{align*}\m{a}+\m{b}:=\bmat{a_1+b_1\\\vdots\\a_n+b_n}\end{align*}
で定義する.
これは高校数学で学ぶ成分で表されたベクトルの和と考え方は同じですね.
列ベクトルの和の具体例
$\m{a},\m{b}\in\R^3$を$\m{a}=\bmat{1\\0\\-2}$, $\m{b}=\bmat{2\\-1\\3}$で定める.$\m{a}+\m{b}$を計算せよ.
列ベクトルの和は各成分で和を計算したものなので,
\begin{align*}\m{a}+\m{b}=\bmat{1+2\\0+(-1)\\-2+3}=\bmat{3\\-1\\1}\end{align*}
である.
また,各成分で交換法則を使えば
\begin{align*}\m{a}+\m{b}=\bmat{a_1+b_1\\\vdots\\a_n+b_n}=\bmat{b_1+a_1\\\vdots\\b_n+a_n}=\m{b}+\m{a}\end{align*}
と列ベクトルの和でも交換法則が成り立つことが分かりますね.
列ベクトルのスカラー倍$k\m{a}$の定義・具体例
列ベクトルのスカラー倍は各成分ごとにスカラー倍を計算してできる列ベクトルと定義されます.
列ベクトルのスカラー倍の定義
$n$次列ベクトル$\m{a}=\bmat{a_1\\\vdots\\a_n}$と実数$k$に対して,$k$を$\m{a}$にかけてできる$n$次実列ベクトル$k\m{a}$を
\begin{align*}k\m{a}:=\bmat{ka_1\\\vdots\\ka_n}\end{align*}
で定義する.
これも高校数学で学ぶ成分で表されたベクトルの実数倍と同じですね.
ただし,$k<0$の場合には$\m{a}$と$k\m{a}$は逆向きになります.すなわち,逆向きに伸び縮みさせると考えます.
列ベクトルのスカラー倍の具体例
$\m{a}\in\R^3$を$\m{a}=\bmat{-2\\3\\1}$で定める.$2\m{a}$を計算せよ.
列ベクトルのスカラー倍は各成分でスカラー倍を計算したものなので,
\begin{align*}2\m{a}=\bmat{2\cdot(-2)\\2\cdot3\\2\cdot1}=\bmat{-4\\6\\2}\end{align*}
である.
また,各成分で結合法則を使えば,$k,\ell\in\R$に対して
\begin{align*}(k\ell)\m{a}=\bmat{(k\ell)a_1\\\vdots\\(k\ell)a_n}=\bmat{k(\ell a_1)\\\vdots\\k(\ell a_n)}=k(\ell\m{a})\end{align*}
と列ベクトルのスカラー倍でも結合法則が成り立つことが分かりますね.
逆ベクトルの定義
$\m{a}\in\R^n$に対して,
\begin{align*}\m{a}+\m{b}=\m{0}\end{align*}
を満たす$n$次列ベクトル$\m{b}$を$\m{a}$の逆ベクトル(inverse vector)といい$-\m{a}$と表します.成分を考えれば$-\m{a}=(-1)\m{a}$であることが分かりますね.
また,$n$次実列ベクトル$\m{x},\m{y}$に対して,$\m{x}+(-\m{y})$を$\m{x}-\m{y}$と表します.
列ベクトルの和は交換法則を満たすので,「$\m{b}+\m{a}=\m{0}$を満たす$\m{b}\in\R^n$を逆ベクトル」と定めても同じことですね.
平行の定義
零ベクトル$\m{0}$でない$\m{a},\m{b}\in\R^n$が平行であるとは
\begin{align*}k\m{a}=\m{b}\end{align*}
を満たす$k\in\R$が存在することをいいます.
図形的には$\m{a},\m{b}\in\R^{n}$が平行であるとは「$\m{a}$を伸び縮みだけで$\m{b}$に一致させられること」と言えますね.
列ベクトルの行列倍$A\m{x}$の定義・具体例
前回の記事の序盤で,線形代数では
\begin{align*}\begin{cases}y_1=x_1+2x_2+3x_3\\y_2=4x_1+5x_2+6x_3\end{cases}\end{align*}
は右辺を係数部分と変数部分に分けて
\begin{align*}\bmat{y_1\\y_2}=\bmat{1&2&3\\4&5&6}\bmat{x_1\\x_2\\x_3}\end{align*}
と表すことを説明しました.
列ベクトルの行列倍の定義
実はいまの右辺は行列$\bmat{1&2&3\\4&5&6}$を列ベクトル$\bmat{x_1\\x_2\\x_3}$に左からかけたものと考えており,列ベクトルの行列倍は一般に以下のように定義されます.
$n$次列ベクトル$\m{x}=\bmat{x_1\\\vdots\\x_n}$と$m\times n$行列$A=\bmat{a_{11}&\dots&a_{1n}\\\vdots&\ddots&\vdots\\a_{m1}&\dots&a_{mn}}$に対して,$A$を$\m{x}$に左からかけてできる$m$次実列ベクトル$A\m{x}$を
\begin{align*}A\m{x}:=\bmat{a_{11}x_1+\dots+a_{1n}x_n\\\vdots\\a_{m1}x_1+\dots+a_{mn}x_n}\end{align*}
で定義する.
$(\text{行列$A$の列数})=(\text{列ベクトル$\m{x}$の次数})$となっている場合のみベクトル$\m{x}$に左から$A$をかけることができます.
列ベクトルの行列倍の具体例
次の各場合の行列$A$と列ベクトル$\m{x}$に対して,$A\m{x}$は定義できるか.また,定義できるときは計算せよ.
- $A=\bmat{1&2&3\\4&5&6}$, $\m{x}=\bmat{x\\y\\z}$
- $A=\bmat{1&2\\3&4\\5&6}$, $\m{x}=\bmat{-1\\2}$
- $A=\bmat{1&2&3\\4&5&6}$, $\m{x}=\bmat{-1\\2}$
(1)の解答
$A=\bmat{1&2&3\\4&5&6}$の列数と$\m{x}=\bmat{x\\y\\z}$の次数はともに3なので,$A\m{x}=\bmat{1&2&3\\4&5&6}\bmat{x\\y\\z}$が定義できて,
\begin{align*}A\m{x}=\bmat{1&2&3\\4&5&6}\bmat{x\\y\\z}
=\bmat{x+2y+3z\\4x+5y+6z}\end{align*}
ですね.
(2)の解答
$A=\bmat{1&2\\3&4\\5&6}$の列数と$\m{x}=\bmat{-1\\2}$の次数はともに2なので,$A\m{x}=\bmat{1&2\\3&4\\5&6}\bmat{-1\\2}$が定義できて,
\begin{align*}A\m{x}=\bmat{1&2\\3&4\\5&6}\bmat{-1\\2}
=\bmat{1\cdot(-1)+2\cdot2\\3\cdot(-1)+4\cdot2\\5\cdot(-1)+6\cdot2}
=\bmat{3\\5\\7}\end{align*}
ですね.
(3)の解答
$A=\bmat{1&2&3\\4&5&6}$の列数は3で,$\m{x}=\bmat{-1\\2}$の次数は2なので,
\begin{align*}A\m{x}=\bmat{1&2&3\\4&5&6}\bmat{-1\\2}\end{align*}
は定義されない.
行列の計算(和・スカラー倍・積)
それでは次に行列の計算の定義に移ります.
行列の和$A+B$とスカラー倍$kA$の定義・具体例
行列の和・スカラー倍は各成分ごとに和・スカラー倍を計算してできる行列と定義されます.
行列の和とスカラー倍の定義
$m\times n$行列$A=(a_{ij})$, $B=(b_{ij})$と$k\in\R$に対して,和$A+B$と$A$の$k$倍$kA$をそれぞれ
- $A+B=\bmat{a_{11}+b_{11}&\dots&a_{1n}+ b_{1n}\\\vdots&\ddots&\vdots\\a_{m1}+b_{m1}&\dots&a_{mn}+b_{mn}}$
- $kA=\bmat{ka_{11}&\dots&ka_{1n}\\\vdots&\ddots&\vdots\\ka_{m1}&\dots&ka_{mn}}$
で定義する.
和と差は同じ成分同士で和と差を取れば良く,$k$倍は全ての成分に$k$をかければ良いわけですね.また,$m\times n$行列$A$に対して
\begin{align*}A+B=B+A=O\end{align*}
を満たす$m\times n$実行列$B$を$-A$と表します.つまり,成分を考えれば$-A=(-1)A$ですね.また,$m\times n$実行列$X$, $Y$に対して$X+(-Y)$を$X-Y$と表します.
そもそも列ベクトルは1列の行列だったので,先に考えた列ベクトルの和・スカラー倍はいずれも行列の和・スカラー倍の特別な場合と捉えることができます.
行列の和とスカラー倍の具体例
行列$A$, $B$を$A=\bmat{1&2\\3&6}$, $B=\bmat{-1&3\\1&0}$で定める.$A+B$, $-2A$を計算せよ.
行列の和は各成分で和を計算したものなので,
\begin{align*}A+B=\bmat{1+(-1)&2+3\\3+1&6+0}=\bmat{0&5\\4&6}\end{align*}
である.また,行列のスカラー倍は各成分でスカラー倍を計算したものなので,
\begin{align*}(-2)A=\bmat{(-2)\cdot1&(-2)\cdot2\\(-2)\cdot3&(-2)\cdot6}=\bmat{-2&-4\\-6&-12}\end{align*}
である.
行列の和とスカラー倍に関する性質
行列の和とスカラー倍について,次のように結合法則と分配法則が成り立ちます.
$m\times n$実行列$A$, $B$, $C$と$k,\ell\in\R$に対して,
\begin{align*}&(A+B)+C=A+(B+C),\quad
(k\ell)A=k(\ell A),
\\&k(A+B)=kA+kB,\quad
(k+\ell)A=kA+\ell A\end{align*}
が成り立つ.
また,行列の和と列ベクトルの行列倍について,次のように分配法則が成り立ちます.
$m\times n$実行列$A$, $B$と$\m{x}\in\R^n$に対して,
\begin{align*}(A+B)\m{x}=A\m{x}+B\m{x}\end{align*}
が成り立つ.
いずれも行列とベクトルの成分を文字でおいて計算すれば証明できるので,計算練習のつもりで証明してみてください.
行列の積$AB$の定義・計算の考え方・具体例
行列の和やスカラー倍は各成分ごとに考えれば良いですが,行列の積は少し複雑で次のように定義されます.
$m\times n$行列$A=(a_{ij})$,$n\times \ell$行列$B=(b_{ij})$とする.このとき,積$AB$を以下で定義する.
\begin{align*}AB
:=\bra{\sum_{k=1}^{n} a_{ik}b_{kj}}_{1\leqq i\leqq m,1\leqq j\leqq \ell}
=\bmat{\sum\limits_{k=1}^{n} a_{1k}b_{k1}&\dots&\sum\limits_{k=1}^{n} a_{1k}b_{k\ell}\\
\vdots&\ddots&\vdots\\
\sum\limits_{k=1}^{n} a_{mk}b_{k1}&\dots&\sum\limits_{k=1}^{n} a_{mk}b_{k\ell}}\end{align*}
この定義のままでは読みにくいので,少し丁寧に説明します.
なぜこのように定義するのかについては,のちの「積の定義が複雑な理由」の項で説明します.
計算の考え方
具体的に積$AB$の(1,1)成分,(1,2)成分,(2,1)成分の計算方法を詳しくみてみましょう.
[1]積$AB$の$(1,1)$成分を求めるには$A$の第1行と$B$の第1列に注目します.
\begin{align*}\bmat{\color{blue}\m{a}_{11}&\color{blue}\m{\dots}&\color{blue}\m{a}_{1n}\\\vdots&\ddots&\vdots\\a_{m1}&\dots&a_{mn}}
\bmat{\color{blue}\m{b}_{11}&\dots&b_{1\ell}\\\color{blue}\m{\vdots}&\ddots&\vdots\\\color{blue}\m{b}_{n1}&\dots&b_{n\ell}}\end{align*}
これらの各成分を順番にかけて足し合わせた$a_{11}b_{11}+a_{12}b_{21}+\dots+a_{1n}b_{n1}\bra{=\sum_{k=1}^{n} a_{1k}b_{k1}}$が積$AB$の$(1,1)$成分です:
\begin{align*}AB=\bmat{\color{blue}\sum\limits_{k=1}^{n} a_{1k}b_{k1}&\dots&*\\\vdots&\ddots&\vdots\\ *&\dots&*}.\end{align*}
[2]積$AB$の$(1,2)$成分を求めるには$A$の第1行と$B$の第2列に注目します.
\begin{align*}\bmat{\color{blue}\m{a}_{11}&\color{blue}\m{\dots}&\color{blue}\m{a}_{1n}\\\vdots&\ddots&\vdots\\a_{m1}&\dots&a_{mn}}
\bmat{b_{11}&\color{blue}\m{b}_{12}&\dots&b_{1\ell}\\\vdots&\color{blue}\m{\vdots}&\ddots&\vdots\\b_{n1}&\color{blue}\m{b}_{n2}&\dots&b_{n\ell}}\end{align*}
これらの各成分を順番にかけて足し合わせた$a_{11}b_{12}+a_{12}b_{22}+\dots+a_{1n}b_{n2}\bra{=\sum_{k=1}^{n} a_{1k}b_{k2}}$が積$AB$の$(1,2)$成分です:
\begin{align*}AB=\bmat{*&\color{blue}\sum\limits_{k=1}^{n} a_{1k}b_{k2}&\dots&*\\\vdots&\vdots&\ddots&\vdots\\ *&*&\dots&*}.\end{align*}
[3]積$AB$の$(2,1)$成分を求めるには$A$の第2行と$B$の第1列に注目します.
\begin{align*}\bmat{a_{11}&\dots&a_{1n}\\\color{blue}\m{a}_{21}&\color{blue}\m{\dots}&\color{blue}\m{a}_{2n}\\\vdots&\ddots&\vdots\\a_{m1}&\dots&a_{mn}}
\bmat{\color{blue}\m{b}_{11}&\dots&b_{1\ell}\\\color{blue}\m{\vdots}&\ddots&\vdots\\\color{blue}\m{b}_{n1}&\dots&b_{n\ell}}\end{align*}
これらの各成分を順番にかけてできる$a_{21}b_{11}+a_{22}b_{21}+\dots+a_{2n}b_{n1}\bra{=\sum_{k=1}^{n} a_{2k}b_{k1}}$が積$AB$の$(2,1)$成分です:
\begin{align*}AB=\bmat{*&\dots&*\\\color{blue}\sum\limits_{k=1}^{n} a_{2k}b_{k1}&\dots&*\\\vdots&\ddots&\vdots\\ *&\dots&*}.\end{align*}
[1]〜[3]のように,積$AB$の$(i,j)$成分を求めるには$A$の第$i$行と$B$の第$j$列に注目して,同様に計算すればいいわけですね.
具体例
$A=\bmat{1&2\\3&6}$, $B=\bmat{-1&3\\1&0}$, $C=\bmat{2&0\\-1&0}$に対して,$AB$, $BA$, $AC$を計算せよ.
行列の積の定義より
\begin{align*}&AB=\bmat{1\cdot(-1)+2\cdot1&1\cdot3+2\cdot0\\3\cdot(-1)+6\cdot1&3\cdot3+6\cdot0}=\bmat{1&3\\3&9},
\\&BA=\bmat{(-1)\cdot1+3\cdot3&(-1)\cdot2+3\cdot6\\1\cdot1+0\cdot3&1\cdot2+0\cdot6}=\bmat{8&16\\1&2},
\\&AC=\bmat{1\cdot2+2\cdot(-1)&1\cdot0+2\cdot0\\3\cdot2+6\cdot(-1)&3\cdot0+6\cdot0}=\bmat{0&0\\0&0}\end{align*}
である.
この例では$AB\neq BA$, $AC=O$となっています.このように,
ということに注意してください.
この点は実数の積と大きく異なる部分ですね.
積の定義が複雑な理由
行列と列ベクトルの積については,定義から
- $n\times\ell$行列$B$を左から$\m{x}\in\R^\ell$にかけて$B\m{x}\in\R^n$
- さらに左から$m\times n$行列$A$をかけると$A(B\m{x})\in\R^m$
となります:
さて,ここで行列$A$と$B$の積$AB$をするとき,結合法則$A(B\m{x})=(AB)\m{x}$が成り立っていて欲しいと思うのは自然なことですね.
たとえば,$A=\bmat{2&2\\-3&1}$, $B=\bmat{-2&0\\3&1}$, $\m{x}=\bmat{x\\y}$の場合を考えると,
\begin{align*}A(B\m{x})
&=A\bra{\bmat{-2&0\\3&1}\bmat{x\\y}}
=A\bmat{-2x\\3x+y}
\\&=\bmat{2&2\\-3&1}\bmat{-2x\\3x+y}
=\bmat{2(-2x)+2(3x+y)\\-3(-2x)+(3x+y)}
\\&=\bmat{2x+2y\\9x+y}
=\bmat{2&2\\9&1}\bmat{x\\y}
=\bmat{2&2\\9&1}\m{x}\end{align*}
となるので,$AB=\bmat{2&2\\9&1}$と定義されていれば,結合法則$A(B\m{x})=(AB)\m{x}$が成り立ちます.このように,行列の積が結合法則をもつように定義しようとすると,上の行列の積の定義のようになるわけですね.
したがって,行列の積と列ベクトルの行列倍について,次のように結合法則が成り立ちます.
$m\times n$行列$A$,$n\times \ell$行列$B$と$\m{x}\in\R^\ell$に対して,
\begin{align*}A(B\m{x})=(AB)\m{x}\end{align*}
が成り立つ.
この性質も行列とベクトルの成分を文字でおいて計算すれば証明できます.
行列のブロック分割と行列の積
ベクトルで区分けされた行列の積を計算することはよくあります.次の命題は計算上便利でよく使われます.
$m\times n$行列$A=(a_{ij})$,$n\times\ell$行列$B=(b_{ij})$を
\begin{align*}A=\bmat{\m{a}_1\\\vdots\\\m{a}_m},\quad
B=[\m{b}_1,\dots,\m{b}_{\ell}]\end{align*}
とベクトルで区分けすると,
\begin{align*}AB=\bmat{\m{a}_1\m{b}_1&\dots&\m{a}_1\m{b}_\ell\\\vdots&\ddots&\vdots\\\m{a}_m\m{b}_1&\dots&\m{a}_m\m{b}_\ell}
=[A\m{b}_1,\dots,A\m{b}_\ell]
=\bmat{\m{a}_1B\\\vdots\\\m{a}_{m}B}\end{align*}
が成り立つ.
$A$, $B$両方をブロック分割した場合の積$AB$
$A$, $B$の区分けの仕方から,
\begin{align*}\m{a}_i=[a_{i1},\dots,a_{in}],\quad
\m{b}_{j}=\bmat{b_{1j}\\\vdots\\b_{nj}}\end{align*}
であることに注意する($i=1,2,\dots,m$, $j=1,2,\dots,\ell$).
また,定義から積$AB$の$(i,j)$成分は$\sum_{k=1}^{n}a_{ik}b_{kj}$であり,これは
\begin{align*}\sum_{k=1}^{n}a_{ik}b_{kj}=a_{i1}b_{1j}+\dots+a_{in}b_{nj}=\m{a}_i\m{b}_{j}\end{align*}
と変形できるから,$AB=\bmat{\m{a}_1\m{b}_1&\dots&\m{a}_1\m{b}_\ell\\
\vdots&\ddots&\vdots\\
\m{a}_m\m{b}_1&\dots&\m{a}_m\m{b}_\ell}$が成り立つ.
$B$のみをブロック分割した場合の積$AB$
最初の等式の第$j$列は
\begin{align*}\bmat{\m{a}_1\m{b}_j\\\vdots\\\m{a}_m\m{b}_j}=\bmat{\m{a}_1\\\vdots\\\m{a}_m}\m{b}_j=A\m{b}_j\end{align*}
だから,積$AB$は$AB=[A\m{b}_1,\dots,A\m{b}_\ell]$と表せる.
$A$のみをブロック分割した場合の積$AB$
同様に,最初の等式の第$i$行は
\begin{align*}[\m{a}_i\m{b}_1,\dots,\m{a}_i\m{b}_\ell]=\m{a}_i[\m{b}_1,\dots,\m{b}_\ell]=\m{a}_iB\end{align*}
だから,積$AB$は$AB=\bmat{\m{a}_1B\\\vdots\\\m{a}_{m}B}$と表せる.
行列の積の結合法則
上でみた行列の積と列ベクトルの行列倍に関する結合法則
\begin{align*}A(B\m{x})=(AB)\m{x}\end{align*}
といま示した命題を併せると,行列の積の結合法則が成り立つことが簡単に証明できます.
$m\times n$行列$A$,$n\times \ell$行列$B$,$\ell\times k$行列$C$に対して,
\begin{align*}A(BC)=(AB)C\end{align*}
が成り立つ.
行列$C$を$C=[\m{c}_1,\dots,\m{c}_k]$と区分けすると,
\begin{align*}A(BC)&=A(B[\m{c}_1,\dots,\m{c}_{k}])=A[B\m{c}_1,\dots,B\m{c}_k]
\\&=[A(B\m{c}_1),\dots,A(B\m{c}_k)]=[(AB)\m{c}_1,\dots,(AB)\m{c}_k]
\\&=(AB)[\m{c}_1,\dots,\m{c}_k]=(AB)C\end{align*}
を得る.



コメント