例えば,正方行列$A=\bmat{1&2\\2&1}$に対して,正則行列$P=\bmat{1&1\\1&-1}$を用意すると,
\begin{align*}P^{-1}AP=\bmat{3&0\\0&-1}\end{align*}
と$P^{-1}AP$は対角行列となります.
このように,正方行列$A$に対して,うまく正則行列$P$を用意して$P^{-1}AP$を対角行列にすることを,正方行列$A$の対角化といいます.
実は「正方行列の対角化があることによって線形代数が広く応用される分野になっている」と言ってもよいくらい,正方行列の対角化は非常に応用範囲が広く,線形代数の中でも特に重要です.
この記事では
- 対角化と対角化の応用例
- 対角化と固有値・固有ベクトル
- 固有値,固有ベクトルの図形的な意味
を順に説明します.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
対角化と対角化の応用例
まずは正方行列$A$の冪$A^k$の計算に対角化が利用できることを説明します.
行列の冪と対角行列
例えば,$A=\bmat{1&2\\3&4}$とすると,
\begin{align*}A^2=&A\cdot A
=\bmat{1\cdot1+2\cdot3&1\cdot2+2\cdot4\\3\cdot1+4\cdot3&3\cdot2+4\cdot4}
=\bmat{7&10\\15&22},
\\A^3=&A^2\cdot A
=\bmat{7\cdot1+10\cdot3&7\cdot2+10\cdot4\\15\cdot1+22\cdot3&15\cdot2+22\cdot4}
=\bmat{37&54\\81&118},
\\A^4=&A^3\cdot A=\dots\end{align*}
と計算することができますが,この計算を見れば分かるように一般に正方行列$A$の冪$A^k$を直接計算するのはとても面倒です.
一方,対角行列$B=\bmat{2&0&0\\0&-1&0\\0&0&1}$の冪$B^k$は
\begin{align*}&B^2=\bmat{4&0&0\\0&1&0\\0&0&1},\quad
B^3=\bmat{8&0&0\\0&-1&0\\0&0&1},\quad
B^4=\bmat{16&0&0\\0&1&0\\0&0&1}\end{align*}
のように対角行列の冪は簡単に計算することができます.一般に次が成り立ちます.
対角行列$X=\bmat{\lambda_1&0&\dots&0\\0&\lambda_2&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&\lambda_n}$に対して,$X^k=\bmat{{\lambda_1}^k&0&\dots&0\\0&{\lambda_2}^k&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&{\lambda_n}^k}$($k=1,2,\dots$)が成り立つ.
数学的帰納法により示す.$k=1$のときに成り立つことは明らかで,ある$k$で成り立つとすると
\begin{align*}X^{k+1}=X^{k}X
=&\bmat{{\lambda_1}^k&0&\dots&0\\0&{\lambda_2}^k&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&{\lambda_n}^k}
\bmat{\lambda_1&0&\dots&0\\0&\lambda_2&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&\lambda_n}
\\=&\bmat{{\lambda_1}^{k+1}&0&\dots&0\\0&{\lambda_2}^{k+1}&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&{\lambda_n}^{k+1}}\end{align*}
となって$k+1$でも成り立つ.
つまり,「対角行列の$k$乗は対角成分を$k$乗した対角行列になる」というわけですね.
対角化と行列の冪
対角行列の冪が簡単に計算できることを用いて,一般の正方行列$A$の冪$A^k$を(直接計算するより)簡単に計算する方法を考えましょう.
$n$次正方行列$A$に対して,$B=P^{-1}AP$が成り立つような$n$次対角行列$B$と$n$次正則行列$P$が得られたとします.
このとき,両辺を$k$乗($k=1,2,\dots$)すると,行列の積の結合法則から
\begin{align*}B^k&=(P^{-1}AP)^k
\\&=(P^{-1}AP)(P^{-1}AP)\dots(P^{-1}AP)
\\&=P^{-1}A(PP^{-1})A(PP^{-1})A\dots A(PP^{-1})AP
\\&=P^{-1}AAA\dots AAP
\\&=P^{-1}A^kP\end{align*}
が成り立ちます.正方行列$A$の間にできている$PP^{-1}$は単位行列となるので,積を計算すると消えて連続した$A$の積になっているわけですね.
このように得られた$B=P^{-1}A^kP$の両辺に左から$P$,右から$P^{-1}$をかけると
\begin{align*}A^k=PB^{k}P^{-1}\end{align*}
が得られます.対角行列$B$の冪$B^k$は簡単に計算でき,もともと$P$は得られているので,$PB^kP^{-1}$を計算すれば,$A^k$が計算できることになりますね.
ここで考えた$B=P^{-1}AP$を次のようにいいます.
[対角化]正方行列$A$に対して,正則行列$P$が存在して$B:=P^{-1}AP$が対角行列となるとき,$A$は$P$により対角化可能であるといい,$B$を$A$の対角化という.
対角化可能な正方行列$A$の冪$A^k$は簡単に計算できる,というのが今説明したことですね.
全ての正方行列が対角化可能であるとは限りません.つまり,$B=P^{-1}AP$を満たす対角行列$B$と正則行列$P$が存在しないこともあります.
対角化と固有値・固有ベクトル
次に正方行列$A$が対角化可能であるときに,どのようなことが成り立つのかを考えます.
対角化可能な正方行列
対角化可能な$n$次正方行列$A$に対して,$B=P^{-1}AP$を満たす対角行列$B$と正則行列$P$が存在するので,
\begin{align*}&B:=\bmat{\lambda_1&0&\dots&0\\0&\lambda_2&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&\lambda_n},
\\&P:=[\m{p}_1,\m{p}_2,\dots,\m{p}_n]\end{align*}
とおきましょう.$B$は対角行列で,$P$は$n$次ベクトル$\m{p}_1,\dots,\m{p}_n$を並べてできた行列ですね.
$B=P^{-1}AP$の両辺に左から$P$をかけると$PB=AP$で,これを列ベクトルを用いて表すと
\begin{align*}[\lambda_1\m{p}_1,\dots,\lambda_n\m{p}_n]=[A\m{p}_1,A\m{p}_2,\dots,A\m{p}_n]\quad\dots(*)\end{align*}
となりますね.ここで,等式$(*)$の各列を比較すると
- $A$の対角化$B$の対角成分の$(i,i)$成分$\lambda_i$
- $A$を対角化させる$P$の第$i$列$\m{p}_i$
は$\lambda_i\m{p}_i=A\m{p}_i$を満たしていますね.
固有値・固有ベクトルの定義
ここで,固有値・固有ベクトルを次のように定義します.
[固有値・固有ベクトル]$n$次正方行列$A$に対して,スカラー$\lambda$と$\m{0}$でない$n$次列ベクトル$\m{p}$が存在して$\lambda\m{p}=A\m{p}$が成り立つとき,$\lambda$を$A$の固有値,$\m{p}$を$A$の固有値$\lambda$に属する固有ベクトルという.
この「固有値」「固有ベクトル」という言葉を用いると,いま説明したことは以下のようになりますね.
[対角化可能な正方行列]$n$次対角行列$A$が$n$次正則行列$P=[\m{p}_1,\dots,\m{p}_n]$によって
\begin{align*}P^{-1}AP=B:=\bmat{\lambda_1&0&\dots&0\\0&\lambda_2&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&\lambda_n}\end{align*}
と対角化されるとき,
- $\lambda_i$は$A$の固有値($i=1,\dots,n$)
- $P$の第$i$列$\m{p}_i$は,$A$の固有値$\lambda_i$に属する固有ベクトル
である:
\begin{align*}&B=P^{-1}AP\iff PB=AP
\\\iff&[\lambda_1\m{p}_1,\lambda_2\m{p}_2,\dots,\lambda_n\m{p}_n]=[A\m{p}_1,A\m{p}_2,\dots,A\m{p}_n]\end{align*}
この意味で,正方行列の対角化は固有値と固有ベクトルと密接に関わっていることになります.
逆に「どのようなときに対角化可能か」を考えるには,固有値・固有ベクトルについての知識が必要です.
固有値・固有ベクトルの図形的な意味
最後に固有値・固有ベクトルの図形的な意味を考えておきましょう.
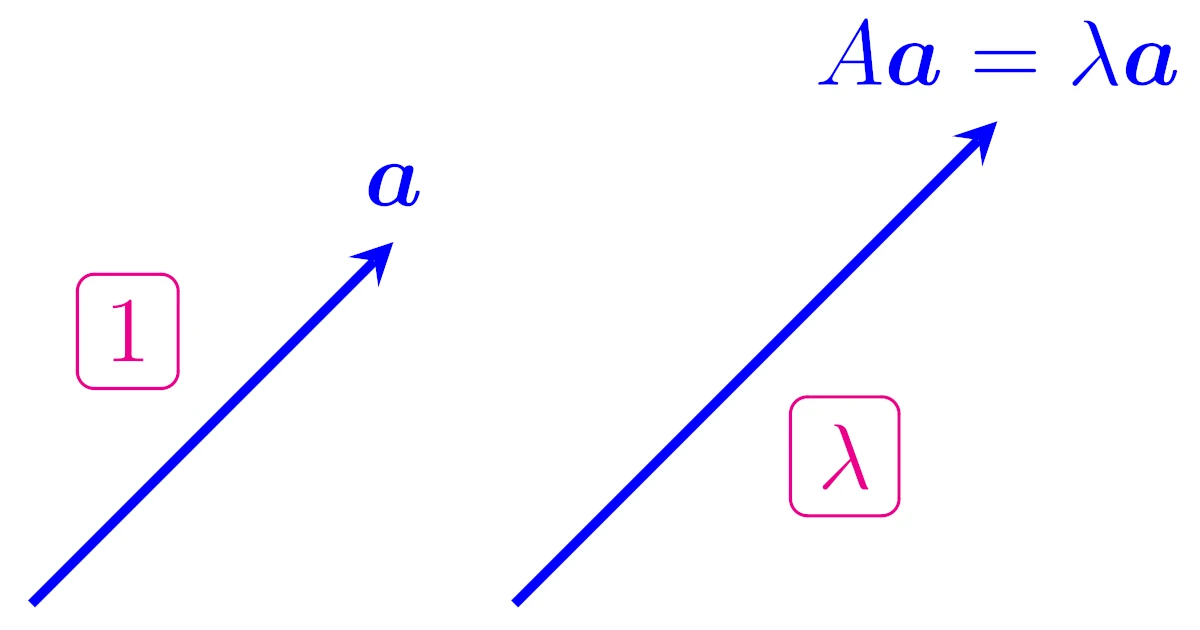
まず$\m{0}$でない$\m{a}\in\R^n$を用意します.
この$\m{a}$に左から$n$次正方行列$A$をかけると$A\m{a}\in\R^n$となりますが,一般にこの$A\m{a}$が$\m{a}$に平行かどうかは分かりません.つまり,$\m{a}$によっては
- 平行になっていなかったり
- $\m{a}$と$A\m{a}$が平行になっていたり
するわけですが,後者のようにうまく$\m{a}$をとって$\m{a}$と$A\m{a}$が平行(または$A\m{a}=\m{0}$)になっていれば,
\begin{align*}A\m{a}=\lambda\m{a}\end{align*}
となる$\lambda\in\R$が存在します.
この等式はまさに固有値と固有ベクトルの定義式で,このときの$\m{a}$を固有ベクトルといい,このときの伸び率$\lambda$を固有値というわけですね.



コメント