例えば,$\R^3$の基底として
\begin{align*}\anb{\bmat{1\\0\\0},\bmat{0\\1\\0},\bmat{0\\0\\1}},\quad\anb{\bmat{1\\1\\1},\bmat{-2\\-2\\1},\bmat{0\\1\\-1}}\end{align*}
などが挙げられます.$\R^3$の他の基底も考えてみると分かってくるのですが,実は$\R^3$の基底はいつでも3個のベクトルからなります.
このことはより一般に成り立ち,任意の$\R^n$の部分空間において基底をなすベクトルの個数は一定であることが証明できます.
そこで,$\R^n$の部分空間$V$の基底をなすベクトルの個数を$V$の次元といいます.
この記事では
- $\R^n$の部分空間の次元の定義
- $\R^n$の部分空間の次元の具体例
- 基底をなすベクトルの個数が一定であることの証明
を順に解説します.
なお,特に断らない限り以下では実行列・実ベクトルを扱うことにしますが,複素行列など一般の体上の行列・ベクトルに対しても同様です.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
$\R^n$の部分空間の次元の定義
冒頭でも説明したように次の定理が成り立ちます(この記事の最後に証明しています).
$\R^n$の部分空間$V$が2つの基底$\anb{\m{a}_1,\m{a}_2,\dots,\m{a}_k}$, $\anb{\m{b}_1,\m{b}_2,\dots,\m{b}_\ell}$をもつとき$k=\ell$が成り立つ.
この定理を踏まえて,次のように次元を定義します.
$\R^n$の部分空間$V$の基底がなすベクトルの個数を$V$の次元(dimension)といい$\dim{V}$と表す.
また,自明な部分空間$\{\m{0}\}$の次元は0と定める.
$\anb{\m{a}_1,\m{a}_2,\dots,\m{a}_r}$が基底なら$\m{a}_1,\m{a}_2,\dots,\m{a}_r$は線形独立なので,直観的には$\m{a}_1,\m{a}_2,\dots,\m{a}_r$たちの線形結合で$r$方向に広がった空間を表せるわけですね.
このことから次元は空間が広がっている「方向」の数を表すといえます.
具体的には$\R^2$が縦・横の2方向,$\R^3$が縦・横・高さの3方向で空間を表現できることからも直観的に受け入れやすいですね.
高校数学でも,平面ベクトルの問題は2つのベクトルを基準,空間ベクトルの問題は3つのベクトルを基準にして考えることが多かったのは,$\R^2$のどの基底も2つのベクトルからなり,$\R^3$のどの基底も3つのベクトルからなることが背景にあるわけですね.
$\R^n$の部分空間の次元の具体例
いくつかの$\R^n$の部分空間について,具体的に次元を求めましょう.
例1($\R^3$の次元)
$\dim{\R^3}$を求めよ.
$\R^3$の基底をひとつ求めて,その基底をなすベクトルの個数が$\R^3$の次元$\dim{\R^3}$である.
前回の記事で証明したように,
\begin{align*}\anb{\bmat{1\\0\\0},\bmat{0\\1\\0},\bmat{0\\0\\1}}\end{align*}
は$\R^3$の基底である.
この基底は3個のベクトルからなるので$\dim{\R^3}=3$である.
一般に$\R^n$は$n$個のベクトルからなる基底
\begin{align*}\anb{\sbmat{1\\0\\\vdots\\0},\sbmat{0\\1\\\vdots\\0},\dots,\sbmat{0\\0\\\vdots\\1}}\end{align*}
をもつので,$\dim{\R^n}=n$となりますね.
この基底を$\R^n$の標準基底というのでした.
例2($\R^2$の1次元部分空間)
$\bmat{x\\y}\in V$は$x-2y=0$を満たすので,$V$を図示すると$xy$平面上の直線$y=\dfrac{1}{2}x$となりますね.
すなわち,$V$は第1成分が第2成分の2倍であるような列ベクトル全部の空間ですから,$V$上の全ての元が$\bmat{2\\1}$の実数倍で表されそうです.
よって,基底として$\anb{\bmat{2\\1}}$がとれて$\dim{V}=1$となりそうです.
$V$の基底をひとつ求めて,その基底をなすベクトルの個数が$V$の次元$\dim{V}$である.
\begin{align*}V&=\set{\bmat{x\\y}\in\R^2}{x-2y=0}
\\&=\set{y\bmat{2\\1}}{y\in\R}
=\spn{\bra{\bmat{2\\1}}}\end{align*}
となり,$V$は$\bmat{2\\1}$により生成される.また,一般に単一の零ベクトルでないベクトルは線形独立だから$\bmat{2\\1}$は線形独立である.
したがって,$\anb{\bmat{2\\1}}$は$V$の基底であり,この基底は1個のベクトルからなるので$\dim{V}=1$である.
直観的には,条件式が1つあることで$\R^2$から次元が1落ちて$\dim{V}=\dim{\R^2}-1=1$となっています.
例3($\R^3$の2次元部分空間)
$\R^3$の部分空間$V$を
\begin{align*}V=\set{\bmat{x\\y\\z}\in\R^3}{x-2y-3z=0}\end{align*}
で定めるとき,$\dim{V}$を求めよ.
$V$を図示すると$xyz$空間上の平面$x-2y-3z=0$となりますね.
$\dim{\R^2}=2$だったように,平面の部分空間は2つのベクトルからなる基底をもち次元は2となりそうです.
$V$の基底をひとつ求めて,その基底をなすベクトルの個数が$V$の次元$\dim{V}$である.
\begin{align*}V&=\set{\bmat{x\\y\\z}\in\R^3}{x-2y-3z=0}
=\set{\bmat{2y+3z\\y\\z}}{y,z\in\R}
\\&=\set{y\bmat{2\\1\\0}+z\bmat{3\\0\\1}}{y,z\in\R}
=\spn{\bra{\bmat{2\\1\\0},\bmat{3\\0\\1}}}\end{align*}
と書き換えられるから,$V$は$\bmat{2\\1\\0},\bmat{3\\0\\1}$により生成される.また,この2つのベクトルを並べてできる行列のランクは
\begin{align*}\rank{\bmat{2&3\\1&0\\0&1}}=\rank{\bmat{1&0\\0&1\\0&0}}=2\end{align*}
だから$\bmat{2\\1\\0},\bmat{3\\0\\1}$は線形独立である.
したがって,$\anb{\bmat{2\\1\\0},\bmat{3\\0\\1}}$は$V$の基底であり,この基底は2個のベクトルからなるので$\dim{V}=2$である.
直観的には,条件式が1つあることで$\R^3$から次元が1落ちて$\dim{V}=\dim{\R^3}-1=2$となっています.
一般に$\m{a}_1,\m{a}_2,\dots,\m{a}_r\in\R^n$が$\rank{[\m{a}_1,\m{a}_2,\dots,\m{a}_r]}=r$を満たせば$\m{a}_1,\m{a}_2,\dots,\m{a}_r$は線形独立なのでした.これについて詳しくは線形独立性と行列のランクについての記事を参照してください.
例4($\R^4$の2次元部分空間)
$\R^4$の部分空間$V$を
\begin{align*}V=\set{\bmat{x\\y\\z\\w}\in\R^4}{\begin{gathered}x+y+3z+4w=0,\\x-y-z+2w=0\end{gathered}}\end{align*}
で定めるとき,$\dim{V}$を求めよ.
例3までが理解できていれば,集合の条件式からベクトルの変数の個数を減らして,どのベクトルで生成されているかを考えれば良さそうですね.
連立1次方程式$\begin{cases}x+y+3z+4w=0\\x-y-z+2w=0\end{cases}$を$x,y$について解くと,
\begin{align*}x=-z-3w,\quad
y=-2z-w\end{align*}
となるので,このとき$\bmat{x\\y\\z\\w}=\bmat{-z-3w\\-2z-w\\z\\w}$だから,
\begin{align*}V&=\set{\bmat{x\\y\\z\\w}\in\R^4}{\begin{gathered}x+y+3z+4w=0,\\x-y-z+2w=0\end{gathered}}
=\set{\bmat{-z-3w\\-2z-w\\z\\w}}{z,w\in\R}
\\&=\set{z\bmat{-1\\-2\\1\\0}+w\bmat{-3\\-1\\0\\1}}{z,w\in\R}
=\spn{\bra{\bmat{-1\\-2\\1\\0},\bmat{-3\\-1\\0\\1}}}\end{align*}
と書き換えられるから,$V$は$\bmat{-1\\-2\\1\\0},\bmat{-3\\-1\\0\\1}$により生成される.また,この2つのベクトルを並べてできる行列のランクは
\begin{align*}\rank{\bmat{-1&-3\\-2&-1\\1&0\\0&1}}=\rank{\bmat{1&0\\0&1\\0&0\\0&0}}=2\end{align*}
だから$\bmat{-1\\-2\\1\\0},\bmat{-3\\-1\\0\\1}$は線形独立である.
したがって,$\anb{\bmat{-1\\-2\\1\\0},\bmat{-3\\-1\\0\\1}}$は$V$の基底であり,この基底は2個のベクトルからなるので$\dim{V}=2$である.
直観的には,線形独立な条件が2つあることで$\R^4$から次元が2落ちて$\dim{V}=\dim{\R^4}-2=2$となっています.
つまり,直観的には空間が広がっている「方向」の数が次元でしたから,(本質的に新しい)条件が1つ加わるごとに空間の「方向」がひとつ減って次元が落ちるわけですね.
基底をなすベクトルの個数が一定であることの証明
それでは最後に冒頭で紹介した次元の定義のもととなった次の定理を証明しましょう.
(再掲)$\R^n$の部分空間$V$が2つの基底$\anb{\m{a}_1,\m{a}_2,\dots,\m{a}_k}$, $\anb{\m{b}_1,\m{b}_2,\dots,\m{b}_\ell}$をもつとき$k=\ell$が成り立つ.
背理法により示す.$k<\ell$と仮定する.
$\m{b}_i$を$\m{a}_1,\dots,\m{a}_k$の線形結合で表す
$\anb{\m{a}_1,\dots,\m{a}_k}$は$V$の基底なので,$\m{b}_1,\dots,\m{b}_k$は$\m{a}_1,\dots,\m{a}_k$の線形結合で表せるから
\begin{align*}\m{b}_i=p_{i1}\m{a}_1+\dots+p_{ik}\m{a}_k\end{align*}
とおく($i=1,\dots,k$).このとき,
\begin{align*}[\m{b}_1,\dots,\m{b}_k]=[\m{a}_1,\dots,\m{a}_k]P\quad
\bra{P:=\bmat{p_{11}&\dots&p_{1k}\\\vdots&\ddots&\vdots\\p_{k1}&\dots&p_{kk}}}\end{align*}
である.
正方行列$P$が正則であることを示す
$\m{b}_1,\dots,\m{b}_k$は線形独立だから,$\rank{[\m{b}_1,\dots,\m{b}_k]}=k$である.よって,行列$[\m{b}_1,\dots,\m{b}_k]$からある$k$行を取り出してできる$k$次正方行列$B$は正則行列となる.
行列$[\m{a}_1,\dots,\m{a}_k]$から同じ$k$行を取り出してできる正方行列を$A$とすると$B=AP$が成り立つ.
もし$P$が正則でなければ$\rank{AP}\le\rank{P}<k$となるので$AP$は正則でない.
これは$B=AP$が正則であることに矛盾するから$P$は正則である.
$\m{b}_{k+1}$が$\m{b}_1,\dots,\m{b}_k$の線形結合で表せることを示す
よって,$[\m{b}_1,\dots,\m{b}_k]=[\m{a}_1,\dots,\m{a}_k]P$の両辺に右から$P^{-1}$をかけて
\begin{align*}[\m{b}_1,\dots,\m{b}_k]P^{-1}=[\m{a}_1,\dots,\m{a}_k]\end{align*}
だから,$\m{a}_1,\dots,\m{a}_k$はいずれも$\m{b}_1,\dots,\m{b}_k$の線形結合で表せる.また,$\anb{\m{a}_1,\dots,\m{a}_k}$は$V$の基底だから$\m{b}_{k+1}\in V$は$\m{a}_1,\dots,\m{a}_k$の線形結合で表せる.
よって,$\m{b}_{k+1}$は$\m{b}_1,\dots,\m{b}_k$の線形結合で表せることになり,$\m{b}_1,\dots,\m{b}_k,\m{b}_{k+1}$が線形独立であることに矛盾する.
$k>\ell$と仮定した場合も同様に矛盾が導かれるから,結局$k=\ell$が得られる.

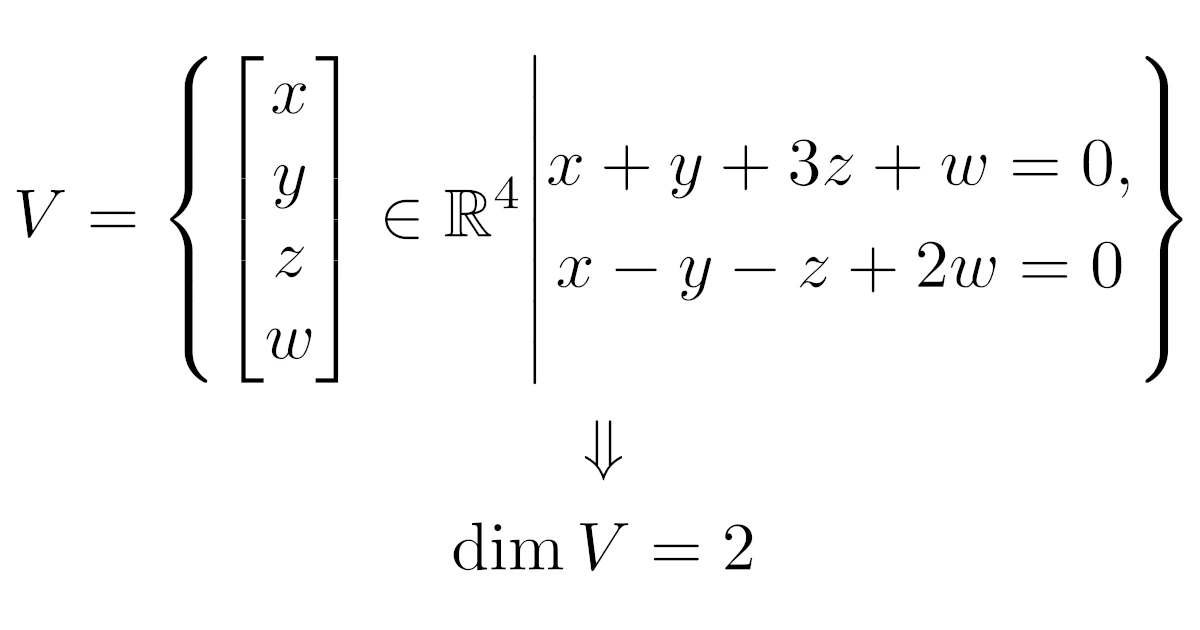


コメント