2次正方行列$A=\bmat{a&b\\c&d}$に対して,
- $A$は正則行列である
- $ad-bc\neq0$が成り立つ
は同値となるのでした.つまり,行列式$ad-bc$が0であるか否かで行列の正則性が判定できるわけですね.この$ad-bc$を$A$の行列式といい,$\det{A}$や$|A|$などと表すのでした.
3次以上の正方行列に対しても行列式が定義でき,0であるか否かで正方行列の正則性が判定できるのですが,3次以上の正方行列の行列式は2次正方行列の行列式ほど簡単ではなく,置換というものを用いる定義が一般的です.
この記事では
- 置換の基礎知識
- 巡回置換と互換
を順に解説します.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
置換の基礎知識
置換の具体例から説明を始め,置換の基礎知識を解説します.また,以下では$n$を2以上の整数とします.
置換の考え方と表し方
置換とは平たく言えば「並べ替える操作」のことをいい,例えば$1,2,3,4$を
\begin{align*}\begin{matrix}1&2&3&4\\\downarrow&\downarrow&\downarrow&\downarrow\\2&3&4&1\end{matrix}\end{align*}
と並べ替える操作$\sigma$は置換です.また,この置換$\sigma$を$\pmat{1&2&3&4\\2&3&4&1}$と表します.他にも,$1,2,3,4,5$を
\begin{align*}\begin{matrix}1&2&3&4&5\\\downarrow&\downarrow&\downarrow&\downarrow&\downarrow\\2&3&5&4&1\end{matrix}\end{align*}
と並べ替える置換$\tau$は$\pmat{1&2&3&4&5\\2&3&5&4&1}$と表します.この置換では4は4のままですが,このように並べ換えないものがあっても構いません.
一般に$\{1,2,\dots,n\}$を並べ替える操作を$\{1,2,\dots,n\}$の置換といいます.
置換の定義
ここで,置換の厳密な定義を述べておきます.
一般の置換を定義するには集合論の「全単射」という言葉を用いることになります.「全単射」を知らなくても直観的に上のように理解していれば一旦は問題ありません.
全単射$\sigma:\{1,2,\dots,n\}\to\{1,2,\dots,n\}$を$\{1,2,\dots,n\}$の置換(permutation)といい,
\begin{align*}\sigma=\pmat{1&2&\dots&n\\\sigma(1)&\sigma(2)&\dots&\sigma(n)}\end{align*}
と表し,$\{1,2,\dots,n\}$の置換全体の集合を$S_n$と表す.
例えば,$\{1,2,3\}$の置換$\sigma$を$\sigma=\pmat{1&2&3\\2&3&1}$で定めると,
\begin{align*}&\sigma(1)=2,\quad\sigma(2)=3,\quad\sigma(3)=1\end{align*}
であり,$\{1,2,3,4\}$の置換$\tau$を$\tau=\pmat{1&2&3&4\\4&3&2&1}$で定めると,
\begin{align*}\tau(1)=4,\quad\tau(2)=3,\quad\tau(3)=2,\quad\tau(4)=1\end{align*}
というわけですね.
また,何も置き換えない置換を単位置換といい,例えば$\{1,2,3,4\}$の単位置換は$\pmat{1&2&3&4\\1&2&3&4}$と表せますね.
置換の積と逆置換
置換は関数(写像)なので合成を考えることができますね.
$\{1,2,\dots,n\}$の置換$\sigma,\tau$に対して,写像の合成$\sigma\circ\tau$を$\sigma$と$\tau$の積(product)といい,$\sigma\tau$と表す.
例えば,$\{1,2,3\}$の置換$\sigma,\tau$を$\sigma=\pmat{1&2&3\\2&1&3}$, $\tau=\pmat{1&2&3\\3&1&2}$で定めると,
\begin{align*}\sigma\tau(1)=\sigma(3)=3,\quad\sigma\tau(2)=\sigma(1)=2,\quad\sigma\tau(3)=\sigma(2)=1\end{align*}
なので$\sigma\tau=\pmat{1&2&3\\3&2&1}$であり,
\begin{align*}\tau\sigma(1)=\tau(2)=1,\quad\tau\sigma(2)=\tau(1)=3,\quad\tau\sigma(3)=\tau(3)=2\end{align*}
なので$\tau\sigma=\pmat{1&2&3\\1&3&2}$ですね.
この例からも分かるように,一般に置換の積は可換とは限りません.
$\{1,2,\dots,n\}$の置換$\sigma$に対して$\sigma$の逆写像を逆置換(inverse permutation)といい,$\sigma^{-1}$で表す.
例えば,$\{1,2,3\}$の置換$\sigma=\pmat{1&2&3\\2&3&1}$, $\{1,2,3,4\}$の置換$\tau=\pmat{1&2&3&4\\4&3&2&1}$に対して,
\begin{align*}&\sigma^{-1}=\pmat{2&3&1\\1&2&3}=\pmat{1&2&3\\3&1&2},
\\&\tau^{-1}=\pmat{4&3&2&1\\1&2&3&4}=\pmat{1&2&3&4\\4&3&2&1}\end{align*}
ですね.
$\{1,2,\dots,n\}$の置換全体の集合$S_n$は置換の合成により非可換群となります.この意味で置換の合成を積と呼んでおり,群は群論でも重要な群で$n$次対称群と呼ばれます.
巡回置換と互換
次に置換の中でも重要な置換を説明していきます.
巡回置換はいくつかの数を一つずつ「ずらす」置換
例えば,置換$\pmat{1&2&3&4\\2&3&1&4}$は$\{1,2,3\}$を$1\to2\to3\to1$と巡回させ,4を動かさない置換となっています.このような一部だけを巡回させる置換を巡回置換といいます.
$\{1,2,\dots,n\}$の置換のうち\begin{align*}\pmat{k_1&k_2&\dots&k_{r-1}&k_r&k_{r+1}&\dots&k_n\\k_2&k_3&\dots&k_r&k_1&k_{r+1}&\dots&k_n}\end{align*}の形の置換を巡回置換(cyclic permutation)といい,$(k_1,k_2,\dots,k_r)$と表す.
例えば,$\{1,2,\dots,6\}$の巡回置換$\sigma=(1,2,4)$は,
\begin{align*}\sigma=&\pmat{1&2&4&3&5&6\\2&4&1&3&5&6}
\\=&\pmat{1&2&3&4&5&6\\2&4&3&1&5&6}\end{align*}
です.つまり,$\sigma=(1,2,4)$は$1,2,4$をこの順に1つずつずらし,$3,5,6$を変えない置換ですね.
任意の置換は巡回置換の積で表せる
例えば,$\{1,2,\dots,8\}$の置換$\sigma$を
\begin{align*}\sigma=\pmat{1&2&3&4&5&6&7&8\\3&6&4&1&2&5&8&7}\end{align*}
で定めます.この$\sigma$は以下のように巡回置換の積で表すことができます.
- まず1に繰り返し$\sigma$を施すと,$1\to3\to4\to1$と巡回する.
- $1,3,4$でない$\{1,2,\dots,8\}$の元,例えば2に繰り返し$\sigma$を施すと,$2\to6\to5\to2$と巡回する.
- $1,3,4,2,5,6$でない$\{1,2,\dots,8\}$の元,例えば7に繰り返し$\sigma$を施すと,$7\to8\to7$と巡回する.
このように考えれば,$\sigma=(1,3,4)(2,6,5)(7,8)$として巡回置換の積で表されます.また,巡回置換$(1,3,4)$, $(2,6,5)$, $(7,8)$は入れ替えても等しいですね:
\begin{align*}\sigma&=(1,3,4)(2,6,5)(7,8)=(1,3,4)(7,8)(2,6,5)
\\&=(2,6,5)(1,3,4)(7,8)=(7,8)(1,3,4)(2,6,5)
\\&=(2,6,5)(7,8)(1,3,4)=(7,8)(2,6,5)(1,3,4)\end{align*}
ここで,次の命題を証明します.
$\{1,2,\dots,n\}$の巡回置換$\sigma,\tau$が同じものを巡回させないとき,$\sigma\tau=\tau\sigma$が成り立つ.
もう少しきちんと書くと,「巡回置換$\sigma=(m_1,\dots,m_k),\tau=(m’_1,\dots,m’_\ell)$に対して,$\{m_1,\dots,m_k\}\cap\{m’_1,\dots,m’_\ell\}=\emptyset$なら$\sigma\tau=\tau\sigma$が成り立つ」ということですね.
$\sigma=(m_1,\dots,m_k)$, $\tau=(m’_1,\dots,m’_\ell)$とする.任意に$m\in\{1,2,\dots,n\}$をとる.
- $m\in\{m_1,\dots,m_k\}$のとき,条件から$\tau$は$m$, $\sigma(m)$を巡回させないから,
\begin{align*}\sigma\tau(m)=\sigma(m)=\tau\sigma(m)\end{align*} - $m\in\{m’_1,\dots,m’_\ell\}$のとき,条件から$\sigma$は$m$, $\tau(m)$を巡回させないから,同様に$\sigma\tau(m)=\tau\sigma(m)$
- $m\notin\{m_1,\dots,m_k,m’_1,\dots,m’_\ell\}$のとき
\begin{align*}\sigma\tau(m)=\sigma(m)=m=\tau(m)=\tau\sigma(m)\end{align*}
が成り立つ.よって,任意の$m\in\{1,2,\dots,n\}$に対して$\sigma\tau(m)=\tau\sigma(m)$が成り立つから,$\sigma\tau=\tau\sigma$が従う.
この命題から,任意の置換が上の置換の例のように巡回置換の積で表せることが分かりますね.
$\{1,2,\dots,n\}$の任意の置換$\sigma$は同じものを巡回させない巡回置換の積で表せる.
互換の定義と巡回置換
ちょうど2つの元を巡回させる巡回置換を互換(transposition)という.
$i,j$を入れ替える互換は,$i,j$を巡回させる巡回置換なので$(i,j)$と表せますね.次は巡回置換と互換の積を結び付ける重要な命題です.
$\{1,2,\dots,n\}$の巡回置換は,$\{1,2,\dots,n\}$の互換の積で表せる.
$\{1,2,\dots,n\}$の任意の巡回置換$\sigma=(m_1,\dots,m_k)$を考える.このとき,$\sigma$が互換$\tau_i:=(m_1,m_i)$($i=2,3,\dots,k$)の積で$\sigma=\tau_k\dots\tau_3\tau_2$と表せることを以下で示す.
任意に$m\in\{1,\dots,n\}$をとる.
- $m=m_i$($i\in\{1,\dots,k-1\}$)と表せるとき
\begin{align*}&\tau_k\dots\tau_{i+1}\tau_i\dots\tau_3\tau_2(m_i)
\\&=\tau_k\dots\tau_i(m_i)=\tau_k\dots\tau_{i+1}(m_1)
\\&=\tau_k\dots\tau_{i+2}(m_{i+1})=m_{i+1}=\sigma(m_i)\end{align*} - $m=m_k$のとき
\begin{align*}\tau_k\tau_{k-1}\dots\tau_3\tau_2(m_k)=\tau_k(m_k)=m_1=\sigma(m_k)\end{align*} - $m$が$m_i$($i\in\{1,\dots,k\}$)のどれとも異なるとき
\begin{align*}\tau_k\tau_{k-1}\dots\tau_3\tau_2(m)=m=\sigma(m)\end{align*}
が成り立つ.よって,任意の$m\in\{1,2,\dots,n\}$に対して$\sigma(m)=\tau_k\dots\tau_3\tau_2(m)$が成り立つから,$\sigma=\tau_k\dots\tau_3\tau_2$が従う.
例えば,巡回置換$\sigma=(1,2,3,4)$は互換の積として,
\begin{align*}\sigma=(3,4)(2,4)(1,4)=(1,2)(2,3)(3,4)\end{align*}
などと表せますね.
置換と互換
ここまでで
- 全ての置換は巡回置換の積で表せる
- 巡回置換は互換の積で表せる
が成り立つことが分かりましたから,これらをまとめて次が従いますね.
$\{1,2,\dots,n\}$の任意の置換は,$\{1,2,\dots,n\}$の互換の積で表せる.
正方行列$A$の置換による行列式$|A|$の定義では置換の符号というものが必要となります.いまの定理は置換の符号を考える際にベースとなる重要な性質となっています.

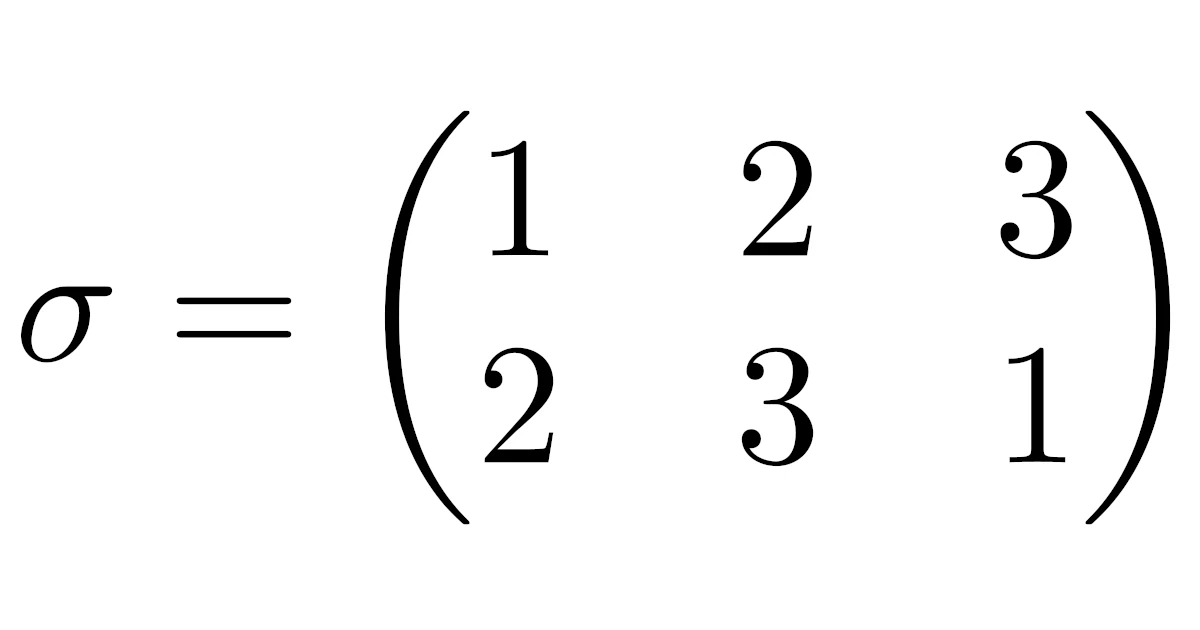


コメント