行列式の図形的イメージ｜正則性が判定できる行列式の考え方

正方行列$A$に対して，$AB=BA=I$となる正方行列$B$が存在するとき，$A$を正則行列といい，$B$を$A$の逆行列といって$A^{-1}$と表すのでした．

正方行列の正則性は線形代数学の様々な概念と繋がっているため，正方行列が正則であるかどうかを判定できることは大切で

行列のランクを用いた判定法
斉次連立１次方程式の非自明解の存在を用いた判定法
ベクトルの線形独立性を用いた判定法

などがありました．

これらと並んで重要な行列式というものを用いた判定法があります．ただし，一般の正方行列の行列式の定義は少々抽象的なので，どういうものか直観的に理解しておくと後々助けになります．

この記事では

２次正方行列の行列式の直観的な解釈
３次以上の正方行列の行列式の直観的な解釈
行列式の性質の直観的な説明

を順に解説します．

なお，この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが，複素行列など一般の体を成分とする行列・ベクトルに対しても同様です．

「線形代数学の基本」の一連の記事

行列と列ベクトル

行列式

$\R^n$の部分空間と基底

正方行列の対角化

２次正方行列の行列式の直観的な解釈

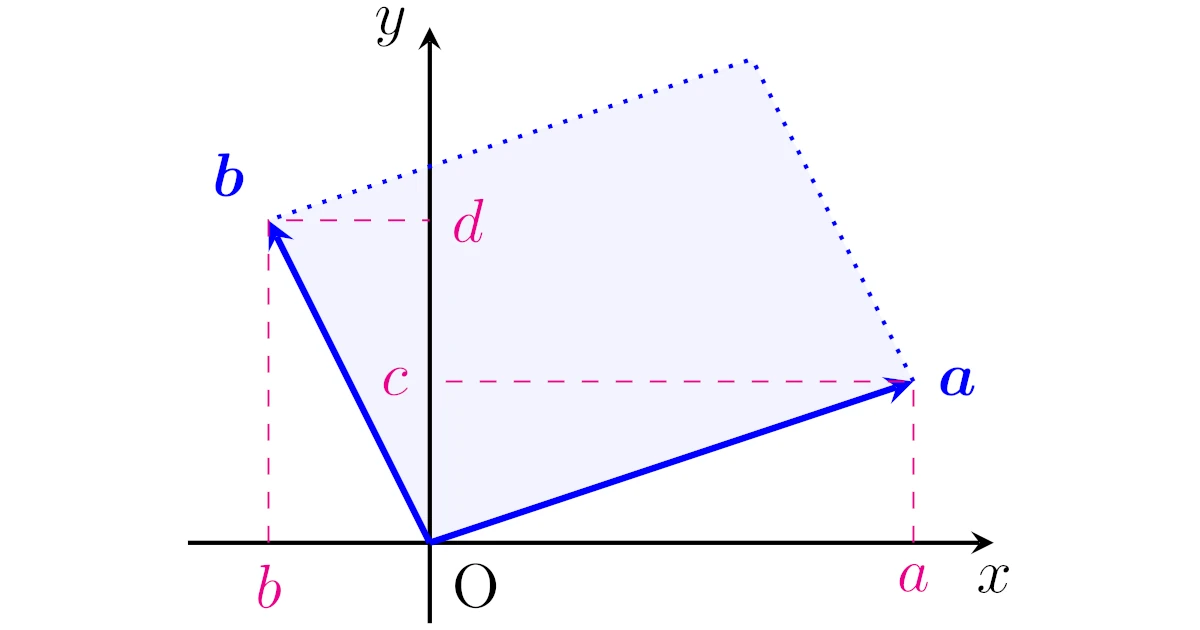
ここでは，２次正方行列$A=\bmat{a&b\\c&d}=[\m{a},\m{b}]$の直観的な考え方を説明します．なお，$\m{a}=\bmat{a\\c}$, $\m{b}=\bmat{b\\d}$ですね．

平行と線形独立

２次正方行列の直観的な考え方を理解するためには，線形独立性についての次の命題がベースになります．

零ベクトルでない２次列ベクトル$\m{a},\m{b}\in\R^2$に対して，次は同値である．

$\m{a}$と$\m{b}$は平行である
$\m{a}$と$\m{b}$は線形従属である

$平行なベクトル２次列ベクトルa,b$

平行であることと，非自明な線形関係をもつことは同値

この命題は３次以上の列ベクトルでも成り立ちますが，ここでは２次正方行列を考えるため２次列ベクトルで述べています．

(1)⇒(2)の証明

$\m{a}$と$\m{b}$が平行なら，$\m{a}=t\m{b}$なる$t\in\R$が存在する．$\m{a}$は零ベクトルでないから$t\neq0$である．

$\m{a}=t\m{b}$を整理した$\m{a}-t\m{b}=\m{0}$は$\m{a}$, $\m{b}$の非自明な線形関係である．よって，$\m{a}$と$\m{b}$は線形従属である．

(2)⇒(1)の証明

$\m{a}$と$\m{b}$が線形従属なら，非自明な線形関係$k\m{a}+\ell\m{b}=\m{0}$が存在する．

もし$k=0$なら$\m{b}\neq\m{0}$と併せて$\ell=0$となるから，$k\m{a}+\ell\m{b}=\m{0}$が非自明な線形関係であることに矛盾する．よって，$k\neq0$である．

よって，$k\m{a}+\ell\m{b}=\m{0}$の両辺を$k$で割って整理すると$\m{a}=-\frac{\ell}{k}\m{b}$となるから$\m{a}$と$\m{b}$は平行である．

この命題の対偶を考えると，

$\m{a}$と$\m{b}$は平行でない
$\m{a}$と$\m{b}$は線形独立である

が同値であると分かりますし，線形独立の「全てのベクトルが完全にバラバラな向きを向いている」というイメージにも合致しますね．

$平行でないベクトル２次列ベクトルa,b$

平行でないことと，自明な線形関係のみもつことは同値

また，一般に零ベクトルを含むベクトルたちは線形従属なので，$\m{a}=\m{0}$または$\m{b}=\m{0}$のとき$\m{a}$, $\m{b}$は線形従属ですね．

２次列ベクトルが張る平行四辺形

２次列ベクトル$\m{a}$, $\m{b}$がつくる以下の平行四辺形を考えましょう．この平行四辺形を「$\m{a}$, $\m{b}$が張る平行四辺形」と呼ぶことにします．

$２次列ベクトルa,bが張る平行四辺形$

原点，$\m{a}$の終点，$\m{b}$の終点，$\m{a}+\m{b}$の終点を頂点とする平行四辺形

ただし，「$\m{a}=\m{0}$または$\m{b}=\m{0}$」もしくは「$\m{a},\m{b}\neq\m{0}$で$\m{a},\m{b}$が平行」のときは，「潰れた」平行四辺形（面積が０）とみなすことにします．

このとき，上で考えたことから

$\m{a}$, $\m{b}$は線形独立である
$\m{a}$, $\m{b}$が張る平行四辺形の面積は０でない

が同値であることが分かります．そこで，「$\m{a}$, $\m{b}$が張る平行四辺形の面積」を$\m{a}$, $\m{b}$の成分$\m{a}=\bmat{a\\c}$, $\m{b}=\bmat{b\\d}$を用いて表しましょう．

平行四辺形の面積と行列式

高校数学で学ぶように，$xy$平面上の三角形の面積は次のようになります．

$xy$平面上の３点$\mathrm{O}(0,0)$, $\mathrm{A}(a,c)$, $\mathrm{B}(b,d)$に対して，

\begin{align*}\tri{OAB}=\frac{1}{2}|ad-bc|\end{align*}

が成り立つ．

$$xy$平面上の3点O(0,0), A(a,c), B(b,d)を頂点とする三角形$

この三角形の面積を2倍すると平行四辺形の面積となる

三角形の面積公式より

\begin{align*}\tri{OAB}&=\frac{1}{2}\mathrm{OA}\cdot\mathrm{OB}\sin{\ang{O}}
\\&=\frac{1}{2}\mathrm{OA}\cdot\mathrm{OB}\sqrt{1-\cos^2{\ang{O}}}
\\&=\frac{1}{2}\sqrt{\mathrm{OA}^2\cdot\mathrm{OB}^2-(\mathrm{OA}\cdot\mathrm{OB}\cdot\cos{\ang{O}})^2}
\\&=\frac{1}{2}\sqrt{|\Ve{OA}|^2|\Ve{OB}|^2-(\Ve{OA}\cdot\Ve{OB})^2}\end{align*}

である．根号の中は

\begin{align*}&|\Ve{OA}|^2|\Ve{OB}|^2-(\Ve{OA}\cdot\Ve{OB})^2
\\&=(a^2+c^2)(b^2+d^2)-(ab+cd)^2
\\&=(a^2b^2+a^2d^2+b^2c^2+c^2d^2)
\\&\quad-(a^2b^2+2abcd+c^2d^2)
\\&=a^2d^2-2abcd+b^2c^2
=(ad-bc)^2\end{align*}

なので，$\tri{OAB}=\frac{1}{2}|ad-bc|$を得る．

この補題より，２次列ベクトル$\m{a}=\bmat{a\\c}$, $\m{b}=\bmat{b\\d}$がなす平行四辺形の面積は$|ad-bc|$と分かりますから，次の定理が成り立ちますね．

２次正方行列$A=\bmat{a&b\\c&d}$に対して，以下は同値である．

$A$は正則行列である．
$ad-bc\neq0$が成り立つ．

２次正方行列の行列式の定義と具体例

以上を踏まえて，２次正方行列の行列式を次のように定義します．

２次正方行列$A=\bmat{a&b\\c&d}$に対し，$ad-bc$を$A$の行列式（determinant）といい，$\det{A}$や$|A|$などと表す．

いくつか具体例を考えましょう．

２次正方行列$A,B,C$を

\begin{align*}A:=\bmat{1&2\\3&4},\quad
B:=\bmat{1&1\\2&2},\quad
C:=\bmat{0&-2\\3&\pi}\end{align*}

と定める．このとき，それぞれ行列式を求め，正則性を判定せよ．

行列式の定義より

\begin{align*}&\det{A}=1\cdot4-2\cdot3=-2,
\\&\det{B}=1\cdot2-1\cdot2=0,
\\&\det{C}=0\cdot\pi-(-2)\cdot3=6\end{align*}

である．行列式が０でないことと，その行列が正則であることは同値なので，$A$, $C$は正則であり$B$は正則でない．

２次正方行列の行列式の正負

$\m{a}=\bmat{a\\c}$, $\m{b}=\bmat{b\\d}$が張る平行四辺形の面積は$|ad-bc|$であり，絶対値の中身の２次正方行列$A=\bmat{a&b\\c&d}$の行列式$\det{A}=ad-bc$は正にも負にもなり得ます．

ところが，２次正方行列$A=[\m{a},\m{b}]$の行列式$\det{A}$の正負は図形的には簡単に判断でき，

$\m{a}$からみて$\m{b}$が反時計回りに180°未満なら$\det{A}>0$
$\m{a}$からみて$\m{b}$が時計回りに180°未満なら$\det{A}<0$

となります．

$2次列ベクトルa,bの位置関係と行列式の正負$

$\m{a}$からみて$\m{b}$がどのように向いているかが$\det{A}$の正負を決める

この意味で行列式$\det{A}=ad-bc$を平行四辺形の符号付き面積ということもあります．

３次以上の正方行列の行列式の直観的な解釈

２次正方行列の行列式の直観的な解釈は３次以上の正方行列に対しても成り立ちます．

３次正方行列の行列式

２次正方行列の場合と同様に，３次正方行列$A=[\m{a},\m{b},\m{c}]$に対しては，$\m{a},\m{b},\m{c}$が張る平行六面体の符号付き体積に相当するものを行列式$\det{A}$, $|A|$と定めれば

$\m{a}$, $\m{b}$, $\m{c}$が線形独立でない
$\det{A}=0$

が同値であることがみてとれますね．

$3次列ベクトルa,b,cの張る平行六面体$

$\m{a}$, $\m{b}$の張る平行四辺形の3次元ver.は平行六面体

つまり，$\m{a}$, $\m{b}$, $\m{c}$が同一平面上にあれば平行六面体は「潰れて」体積が０となりますし，この逆も成り立ちます．

４次以上の正方行列の行列式

４次正方行列以上になると通常は視覚的に分かるように図を描くことは困難ですが，直観的には２次・３次と同様に考えることができます．

一般に，$n$次正方行列$A=[\m{a}_1,\dots,\m{a}_n]$に対しては，$\m{a}_1,\dots,\m{a}_n$がつくる「平行立体の$n$次元体積」に相当するものを行列式$\det{A}$, $|A|$と定めれば，

$\m{a}_1,\dots,\m{a}_n$が線形独立でない
$\det{A}=0$

は同値となります．

ところが，「４次元以上の体積」を考えるのは難しいので，実際の定義では置換を用いた定義を採用することが多いです．置換を用いることで，次数に捉われずに一律に正方行列の行列式を定義することができます．

行列式の性質の直観的な説明

行列式に関する性質のいくつかは，以上の行列式の図形による直観的な解釈から説明できます．そこで，以下では行列式のいくつかの性質を図形的に捉えてみましょう．

厳密な証明はのちの記事で与えます．

行列式の各列の和・スカラー倍はバラバラにできる（行列式の多重線形性）

２次列ベクトル$\m{a},\m{b},\m{c}\in\R^2$と$k\in\R$に対して，

\begin{align*}&\det[\m{a},\m{b}]+\det[\m{a},\m{c}]=\det[\m{a},\m{b}+\m{c}],
\\&\det[\m{a},k\m{b}]=k\det[\m{a},\m{b}]\end{align*}

が成り立ちます．このことを図形的に考えてみましょう．

第１式の直観的な解釈

左辺の各項$\det[\m{a},\m{b}]$, $\det[\m{a},\m{c}]$は$\m{a}$と$\m{b}$のなす平行四辺形の符号付き面積と$\m{a}$と$\m{c}$のなす平行四辺形の符号付き面積です．一方，右辺$\det[\m{a},\m{b}+\m{c}]$は$\m{a}$と$\m{b}+\m{c}$のなす平行四辺形の符号付き面積です．

これらは等積変形を考えると等しいことが見てとれますね．

$a,bが張る平行四辺形，a,cが張る平行四辺形，a,b+cが張る平行四辺形$

$\m{a}$に平行な辺をスライドさせると面積が等しいことが分かる

第２式の直観的な解釈

$\m{b}$を$k$倍すると，辺の長さが変化するので符号付き面積も$k$倍となることが分かりますね．

$a,bが張る平行四辺形，a,kbが張る平行四辺形$

1辺の方向に$k$倍に引き伸ばされる

一般の場合

同様のことは一般の正方行列の行列式でも成り立ち，この性質を行列式の多重線形性といいます．$n$次正方行列の場合は以下のようになります．

$k,\ell\in\R$, $i\in\{1,\dots,n\}$とすると

\begin{align*}&\det[\m{a}_1,\dots,\m{a}_{i-1},k\m{b}_i+\ell\m{c}_i,\m{a}_{i+1},\dots,\m{a}_n]
\\&=k\det[\m{a}_1,\dots,\m{a}_{i-1},\m{b}_i,\m{a}_{i+1},\dots,\m{a}_n]
\\&\quad+\ell\det[\m{a}_1,\dots,\m{a}_{i-1},\m{c}_i,\m{a}_{i+1},\dots,\m{a}_n]\end{align*}

が成り立つ．

２つの列を入れ替えると行列式は−１倍される（行列式の交代性）

$\m{a}=\bmat{a\\c}$, $\m{b}=\bmat{b\\d}$に対して，$\m{a}$からみた$\m{b}$の位置と$\m{b}$からみた$\m{a}$の位置は逆になるので，２次正方行列$\det[\m{a},\m{b}]$, $\det[\m{b},\m{a}]$の正負は逆になることが分かりますね：

\begin{align*}\det[\m{a},\m{b}]=-\det[\m{b},\m{a}].\end{align*}

３次以上の行列式でも同様に２つの列を入れ替えると行列式は−１倍されます．

$\m{a}_1,\dots,\m{a}_n\in\R^n$, $i,j\in\{1,\dots,n\}$とすると

\begin{align*}\det[\m{a}_1,\dots,\m{a}_i,\dots,\m{a}_j,\dots,\m{a}_n]
=-\det[\m{a}_1,\dots,\m{a}_j,\dots,\m{a}_i,\dots,\m{a}_n]\end{align*}

が成り立つ．

この命題は非常に重要な性質で，この命題から例えば２つの列が等しい行列の行列式は０となることが簡単に分かります．

$\m{a}_1,\dots,\m{a}_n\in\R^n$について，ある$i,j\in\{1,\dots,n\}$が存在して$\m{a}_i=\m{a}_j$（$i<j$）が成り立つとする．このとき，

\begin{align*}\det[\m{a}_1,\dots,\m{a}_n]=0\end{align*}

が成り立つ．

交代性と併せて

\begin{align*}\det[\m{a}_1,\dots,\m{a}_i,\dots,\m{a}_j,\dots,\m{a}_n]
&=-\det[\m{a}_1,\dots,\m{a}_j,\dots,\m{a}_i,\dots,\m{a}_n]
\\&=-\det[\m{a}_1,\dots,\m{a}_i,\dots,\m{a}_j,\dots,\m{a}_n]\end{align*}

なので，$2\det[\m{a}_1,\dots,\m{a}_i,\dots,\m{a}_j,\dots,\m{a}_n]=0$である．両辺２で割って$\det[\m{a}_1,\dots,\m{a}_n]=0$を得る．

行列式の図形的イメージ｜正則性が判定できる行列式の考え方

線形代数学の参考文献

大学教養線形代数（加藤文元著）

手を動かしてまなぶ線形代数（藤岡敦著）