正方行列$A$が正則であるかどうかの判定法は様々ありますが，それらのひとつに行列式$|A|$を用いた判定法があり，
- $A$が正則行列であること
- 行列式$|A|$が０でないこと
が同値となります．この(1)⇒(2)の証明は行列式の基本性質から得られ，逆の(2)⇒(1)は余因子を用いて実際に逆行列を表すことで示すことができます．
この記事では
- 正方行列の余因子と余因子展開
- 行列式による正則条件と逆行列
を順に解説します．
なお，この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが，複素行列など一般の体を成分とする行列・ベクトルに対しても同様です．
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
線形代数学の参考文献
以下は線形代数学に関するオススメの教科書です．
大学教養 線形代数（加藤文元 著）
数学科など理論系の学生向けの線形代数の入門書です．平易な例から丁寧に説明されています．
手を動かしてまなぶ 線形代数（藤岡敦 著）
理論と演習のバランスをとりながら勉強したい人にオススメの入門書です．
正方行列の余因子と余因子展開
結論から言えば，正方行列$A$に対して$A$が正則行列であるための必要十分条件は$|A|\neq0$ですが，このことを証明するには余因子を説明する必要があります．
正方行列の余因子の定義
$n$次正方行列$A$に対して，$A$の第$i$行と第$j$列を取り除いてできる${n-1}$次行列の行列式を$(i,j)$小行列式（minor determinant）といい，$(i,j)$小行列式に$(-1)^{i+j}$をかけたものを$(i,j)$余因子（cofactor）という．
この記事では，行列$A=(a_{ij})$の$(i,j)$余因子を$a_{ij}^{*}$と表します．例えば，$A=\bmat{1&2&3\\4&5&6\\7&8&9}$に対して
\begin{align*}&a_{12}^{*}=(-1)^{1+2}\vmat{4&6\\7&9}=6,
\\&a_{33}^{*}=(-1)^{3+3}\vmat{1&2\\4&5}=-3\end{align*}
ですね．
$n$次正方行列$A$に対して，$A$の$(i,j)$余因子$a_{ij}^{*}$は$A$の第$j$列を$\m{e}_{i}$に置き換えてできる行列の行列式に等しい：
\begin{align*}a_{ij}^{*}=|\m{a}_1,\dots,\m{a}_{j-1},\m{e}_{i},\m{a}_{j+1},\dots,\m{a}_n|\end{align*}
行列$[\m{a}_1,\dots,\m{a}_{j-1},\m{e}_i,\m{a}_{j+1},\dots,\m{a}_n]$を
\begin{align*}[\m{a}_1,\dots,\m{a}_{j-1},\m{e}_i,\m{a}_{j+1},\dots,\m{a}_n]=\bmat{A_1&\m{0}&A_2\\\m{p}&1&\m{q}\\A_3&\m{0}&A_4}\end{align*}
とおく．
$\sigma,\tau\in S_{n}$を巡回置換$\sigma:=(1,\dots,j)$, $\tau:=(1,\dots,i)$とすると
\begin{align*}\vmat{A_1&\m{0}&A_2\\\m{p}&1&\m{q}\\A_3&\m{0}&A_4}
&=\sgn{\sigma}\vmat{\m{0}&A_1&A_2\\1&\m{p}&\m{q}\\\m{0}&A_3&A_4}
=\sgn{\sigma}\sgn{\tau}\vmat{1&\m{p}&\m{q}\\\m{0}&A_1&A_2\\\m{0}&A_3&A_4}
\\&=(-1)^{i+j-2}\vmat{A_1&A_2\\A_3&A_4}=(-1)^{i+j}\vmat{A_1&A_2\\A_3&A_4}=a_{ij}^{*}\end{align*}
を得る．
余因子展開
次の命題は余因子展開（cofactor expansion）とよばれ，理論上非常に有用です．
［余因子展開］$n$次正方行列$A=(a_{ij})$の行列式は，任意の$j=1,2,\dots,n$に対して，以下が成り立つ．
\begin{align*}|A|=\sum_{i=1}^{n}a_{ij}a_{ij}^{*}\bra{=a_{1j}a_{1j}^{*}+\dots+a_{nj}a_{nj}^{*}}\end{align*}
$A=[\m{a}_1,\dots,\m{a}_n]$とすると，行列式の線形性と補題より
\begin{align*}|A|&=\abs{\m{a}_1,\dots,\m{a}_{j-1},\sum_{i=1}^{n}a_{ij}\m{e}_{i},\m{a}_{j+1},\dots,\m{a}_n}
\\&=\sum_{i=1}^{n}a_{ij}\abs{\m{a}_1,\dots,\m{a}_{j-1},\m{e}_{i},\m{a}_{j+1},\dots,\m{a}_n}
\\&=\sum_{i=1}^{n}a_{ij}a_{ij}^{*}\end{align*}
を得る．
例えば，$A=(a_{ij})=\bmat{1&2&3\\4&5&6\\7&8&9}$に対して
\begin{align*}|A|&=a_{11}a_{11}^{*}+a_{21}a_{21}^{*}+a_{31}a_{31}^{*}
\\&=1\cdot(-1)^{1+1}\vmat{5&6\\8&9}+4\cdot(-1)^{2+1}\vmat{2&3\\8&9}+7\cdot(-1)^{3+1}\vmat{2&3\\5&6}
\\&=1\cdot(-1)^{2}\cdot(-3)+4\cdot(-1)^{3}\cdot(-6)+7\cdot(-1)^{4}\cdot(-3)
\\&=-3+24-21=0\end{align*}
と余因子展開から行列式$|A|$が計算できるわけですね．
余因子展開は理論上では非常に重要ですが，実際に行列式を計算する際には基本変形による行列式の計算が便利でしょう．
行列式による正則条件と逆行列
余因子を用いることで，次のように正則行列の逆行列を求めることができます．
$n$次正方行列$A$に対して，次は同値である．
- $A$は正則行列
- $|A|\neq0$
さらに，これらの少なくとも一方（すなわち両方）を満たすとき，以下が成り立つ．
\begin{align*}A^{-1}=\frac{1}{|A|}\bmat{a_{11}^{*}&\dots&a_{n1}^{*}\\\vdots&\ddots&\vdots\\a_{1n}^{*}&\dots&a_{nn}^{*}}\end{align*}
正則行列の行列式が０でないことの証明（(1)⇒(2)の証明）
$A$は正則行列であるとする．一般に$n$次正方行列$X$, $Y$に対して，積の行列式$|XY|$と行列式の積$|X||Y|$は等しいので
\begin{align*}|A||A^{-1}|=|AA^{-1}|=|I_n|=1\end{align*}
である．よって，$|A|\neq0$である．
行列式が０でないなら正則行列であることの証明（(2)⇒(1)の証明）
$A=(a_{ij})=[\m{a}_1,\dots,\m{a}_n]$, $B:=\bmat{a_{11}^{*}&\dots&a_{n1}^{*}\\\vdots&\ddots&\vdots\\a_{1n}^{*}&\dots&a_{nn}^{*}}$とすると，積$BA$の第$(i,j)$成分は
\begin{align*}\sum_{k=1}^{n}a_{kj}a_{ki}^{*}
&=\sum_{k=1}^{n}a_{kj}|\m{a}_1,\dots,\m{a}_{i-1},\m{e}_{k},\m{a}_{i+1},\dots,\m{a}_n|
\\&=\abs{\m{a}_1,\dots,\m{a}_{i-1},\sum_{k=1}^{n}a_{kj}\m{e}_{k},\m{a}_{i+1},\dots,\m{a}_n}
\\&=\abs{\m{a}_1,\dots,\m{a}_{i-1},\m{a}_j,\m{a}_{i+1},\dots,\m{a}_n}\end{align*}
である．これは
- $i\neq j$のときは，第$i$列と第$j$列が等しいから行列式の交代性より０に等しい
- $i=j$のときは，$|A|$に等しい
ので$BA=|A|I_n$が成り立つ．$|A|\neq0$なら$\frac{1}{|A|}B$は$A$の逆行列となり，$A$は正則である．
例えば，２次行列$A=(a_{ij})=\bmat{a&b\\c&d}$について
\begin{align*}&a_{11}^{*}=(-1)^{1+1}d=d,\quad
a_{12}^{*}=(-1)^{1+2}c=-c,
\\&a_{21}^{*}=(-1)^{2+1}b=-b,\quad
a_{22}^{*}=(-1)^{2+2}a=a\end{align*}
なので，いまの逆行列の定理から$|A|=ad-bc\neq0$なら$A$は正則で
\begin{align*}A^{-1}&=\frac{1}{|A|}\bmat{a_{11}^{*}&a_{21}^{*}\\a_{12}^{*}&a_{22}^{*}}
\\&=\frac{1}{ad-bc}\bmat{d&-b\\-c&a}\end{align*}
となりますね．これは以前の記事から考えていたものと一致していますね．
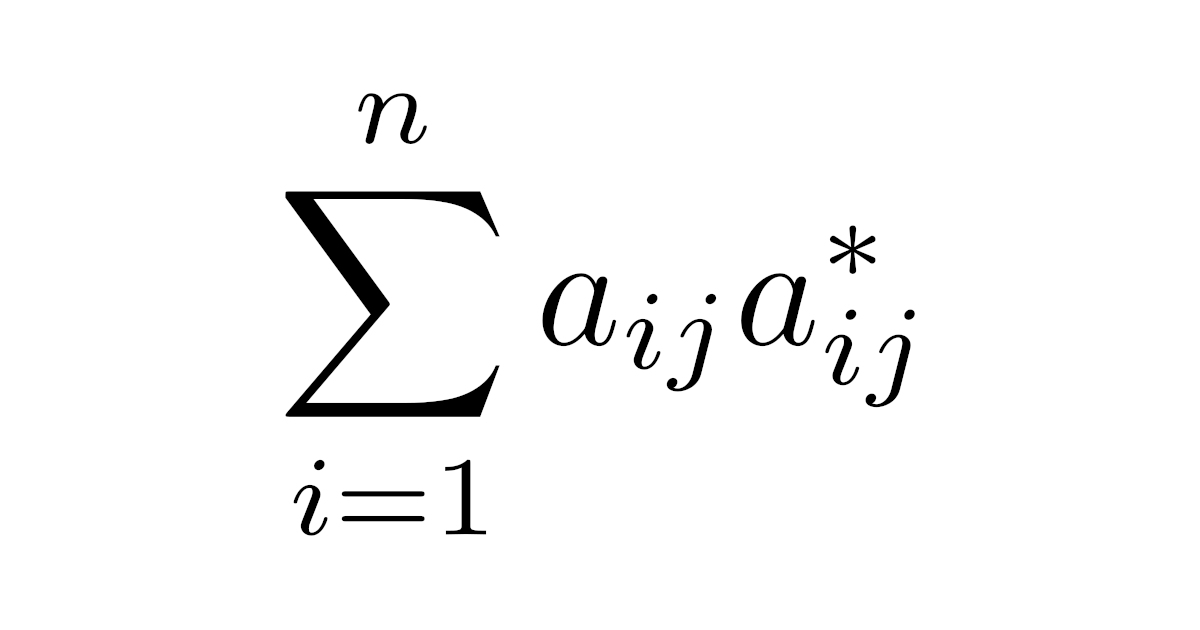
コメント